33 Даны действительные числа x, y. Получить:
34 Даны действительные числа x, y, z. Получить:
35 Даны действительные числа x, y, z. Вычислить:
36 Даны действительные числа a, b, c. Проверить, выполняются ли неравенства a < b < c.
37 Даны действительные числа a, b, c. Удвоить эти числа, если a ≥ b ≥ c, и заменить их абсолютными значениями, если это не так.
38 Даны действительные числа x, y. Вычислить z:
39 Даны два действительных числа. Вывести первое число, если оно больше второго, и оба числа, если это не так.
40 Даны два действительных числа. Заменить первое число нулём, если оно меньше или равно второму, и оставить числа без изменения в противном случае.
41 Даны три действительных числа. Выбрать из них те, которые принадлежат интервалу (1, 3).
42 Даны действительные числа x, y (x не равно y). Меньшее из этих двух чисел заменить их полусуммой, а большее - их удвоенным произведением.
43 Даны три действительных числа. Возвести в квадрат те из них, значения которых неотрицательны.
44 Если сумма трех попарно различных действительных чисел x, y, z меньше единицы, то наименьшее из этих трех чисел заменить полусуммой двух других; в противном случае заменить меньшее из x и y полусуммой двух оставшихся значений.
45 Даны действительные числа a, b, c, d. Если a ≤ b ≤ c ≤ d, то каждое число заменить наибольшим из них; если a > b > c > d, то числа оставить без изменения; в противном случае все числа заменяются их квадратами.
46 Даны действительные числа x, y. Если x и y отрицательны, то каждое значение заменить его модулем; если отрицательно только одно из них, то оба значения увеличить на 0,5; если оба значения неотрицательны и ни одно из них не принадлежит отрезку [0.5, 2.0], то оба значения уменьшить в 10 раз; в остальных случаях x и y оставить без изменения.
47 Даны действительные положительные числа x, y, z.
48 Даны действительные числа a, b, c (a не равно нулю). Выяснить, имеет ли уравнение ax2 + bx + c = 0 действительные корни. Если действительные корни имеются, то найти их. В противном случае ответом должно служить сообщение, что действительных корней нет.
49 Дано действительное число h. Выяснить, имеет ли уравнение ax2 + bx + c = 0 действительные корни, если
50 Даны действительные числа a1, b1, c1, a2, b2, c2. Выяснить, верно ли, что |a1b2 - a2b1| ≥ 0.0001, и если верно, то найти рашение системы линейных уравнений
51 Даны действительные числа a, b, c (a ≠ 0). Полностью исследовать биквадратное уравнение ax4 + bx2 + c = 0, т.е. если действительных корней нет, то должно быть выдано сообщение об этом, иначе должны быть выданы два или четыре корня.
52 Даны действительные числа a, b, c, d, s, t, u (s и t одновременно не равны нулю). Известно, что точки (a, b) и (c, d) не лежат на прямой L, заданной уравнением sx + ty + u = 0 . Прямая L разбивает координатную плоскость на две полуплоскости. Выяснить, верно ли, что точки (a, b) и (c, d) принадлежат разным полуплоскостям.(*)
53 Даны действительные числа a, b, c, d, e, f, g, h. Известно что точки (e, f) и (g, h) различны. Известно также, что точки (a, b) и (c, d) не лежат на прчмой L, проходящей через точки (e, f) и (g, h). Прчмая L разбивает координатную плоскость на две полуплоскости. Выяснить, верно ли, что точки (a, b) и (c, d) принадлежат одной и той же полуплоскости.(**)
54 Даны действительные числа x1, x2, x3, y1, y2, y3. Принадлежит ли начало координат треугольнику с вершинами (x1, y1), (x2, y2), (x3, y3)?
55 Даны действительные положительные числа a, b, c, d. Выяснить можно ли прямоугольник со сторонами a, b уместить внутри прямоугольника со сторонами c, d так, чтобы каждая из сторон одного прчмоугольника была параллельна или перпендикулярна каждой стороне второго прямоугольника.
56 Даны действительные положительные числа a, b, c, x, y. Выяснить, пройдет ли кирпич с ребрами a, b, c в прямоугольное отверстие со сторонами x, y. Просовывать кирпич в отверстие разрешается только так, чтобы каждое из его ребер было параллельно или перпендикулярно каждой из сторон отверстия.
57 Дано действительное число a. Вычислить f(a), если
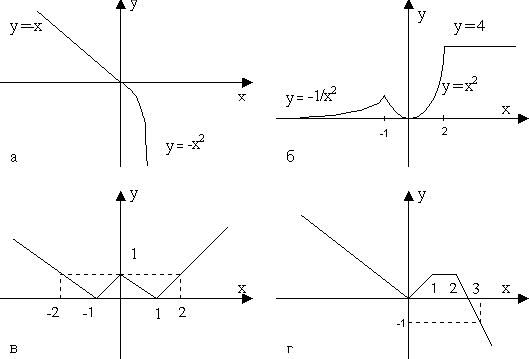
58 Дано действительное число a. Для функции f(x), графики которых представланы на рис.1 а - г, вычислить f(a).
59 Даны действительные числа x, y. Определить, принадлежит ли точка с координатами x, y заштрихованной части плоскости
(рис.2, а - к).
60 Пусть D - заштрихованная часть плоскости (рис.3, а - е) и пусть U определяется по x и y следующим
образом (запись(x, y)Є D означает, что точка с координатами x, y принадлежит D):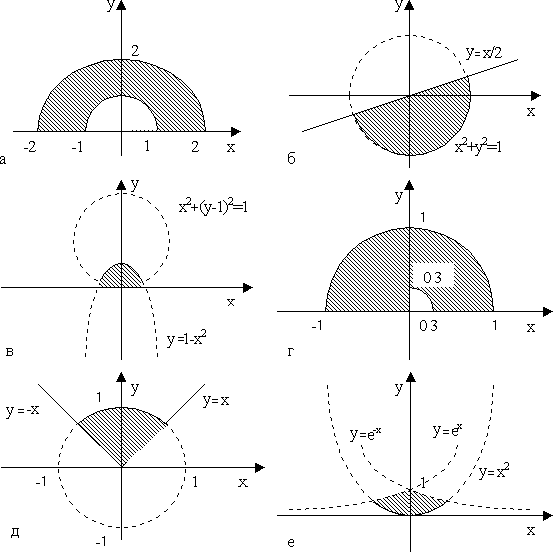
(*) В этой задаче, как и вряде следующих задач, надо воспользоваться тем, что две точки (a, b) и (c, d), не лежащие на прямой, определяемой уравнением sx + ty + u = 0, принадлежат одной полуплоскости, если sa + tb + u и sc + td + u - числа одного знака. Справедлив и более общий факт: если уравнение F(x, y) = 0 определяет прямую или кривую, разбивающую координатную плоскость на две части, то точки (a, b) и (c, d), не лежащие на этой линии, принадлежат одной и той же части плоскости, если F(a, b) и F(c, d) - числа одного знака.
(**) В этой задаче, как и в ряде следующих задач, надо воспользоваться тем, что уравнением прямой, проходящей через две различные точки (e, f) и (g, h), является уравнение (x - e)(h - f) - (y - f)(g - e) = 0.
-
а) max(x, y);
б) min(x, y);
в) max(x, y), min(x, y).
34 Даны действительные числа x, y, z. Получить:
-
а) max(x, y, z);
б) max(x, y, z), min(x, y, z).
35 Даны действительные числа x, y, z. Вычислить:
-
а) max(x + y + z, xyz);
б) max2(x + y + z/2, xyz) + 1.
36 Даны действительные числа a, b, c. Проверить, выполняются ли неравенства a < b < c.
37 Даны действительные числа a, b, c. Удвоить эти числа, если a ≥ b ≥ c, и заменить их абсолютными значениями, если это не так.
38 Даны действительные числа x, y. Вычислить z:
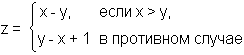
39 Даны два действительных числа. Вывести первое число, если оно больше второго, и оба числа, если это не так.
40 Даны два действительных числа. Заменить первое число нулём, если оно меньше или равно второму, и оставить числа без изменения в противном случае.
41 Даны три действительных числа. Выбрать из них те, которые принадлежат интервалу (1, 3).
42 Даны действительные числа x, y (x не равно y). Меньшее из этих двух чисел заменить их полусуммой, а большее - их удвоенным произведением.
43 Даны три действительных числа. Возвести в квадрат те из них, значения которых неотрицательны.
44 Если сумма трех попарно различных действительных чисел x, y, z меньше единицы, то наименьшее из этих трех чисел заменить полусуммой двух других; в противном случае заменить меньшее из x и y полусуммой двух оставшихся значений.
45 Даны действительные числа a, b, c, d. Если a ≤ b ≤ c ≤ d, то каждое число заменить наибольшим из них; если a > b > c > d, то числа оставить без изменения; в противном случае все числа заменяются их квадратами.
46 Даны действительные числа x, y. Если x и y отрицательны, то каждое значение заменить его модулем; если отрицательно только одно из них, то оба значения увеличить на 0,5; если оба значения неотрицательны и ни одно из них не принадлежит отрезку [0.5, 2.0], то оба значения уменьшить в 10 раз; в остальных случаях x и y оставить без изменения.
47 Даны действительные положительные числа x, y, z.
-
а) Выяснить, существует ли треугольник с длинами сторон x, y, z.
б) Если треугльник существует, то ответить - является ли он остроугльным.
48 Даны действительные числа a, b, c (a не равно нулю). Выяснить, имеет ли уравнение ax2 + bx + c = 0 действительные корни. Если действительные корни имеются, то найти их. В противном случае ответом должно служить сообщение, что действительных корней нет.
49 Дано действительное число h. Выяснить, имеет ли уравнение ax2 + bx + c = 0 действительные корни, если
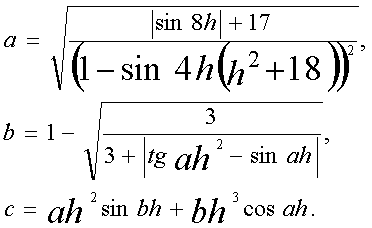
- Если действительные корни существуют, тонайти их. В противном случае
ответом должно служить сообщение, что действительных корней нет.
50 Даны действительные числа a1, b1, c1, a2, b2, c2. Выяснить, верно ли, что |a1b2 - a2b1| ≥ 0.0001, и если верно, то найти рашение системы линейных уравнений
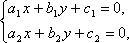
- (при выполнении выписанного неравенства система заведомо совместна и имеет
единственное решение).
51 Даны действительные числа a, b, c (a ≠ 0). Полностью исследовать биквадратное уравнение ax4 + bx2 + c = 0, т.е. если действительных корней нет, то должно быть выдано сообщение об этом, иначе должны быть выданы два или четыре корня.
52 Даны действительные числа a, b, c, d, s, t, u (s и t одновременно не равны нулю). Известно, что точки (a, b) и (c, d) не лежат на прямой L, заданной уравнением sx + ty + u = 0 . Прямая L разбивает координатную плоскость на две полуплоскости. Выяснить, верно ли, что точки (a, b) и (c, d) принадлежат разным полуплоскостям.(*)
53 Даны действительные числа a, b, c, d, e, f, g, h. Известно что точки (e, f) и (g, h) различны. Известно также, что точки (a, b) и (c, d) не лежат на прчмой L, проходящей через точки (e, f) и (g, h). Прчмая L разбивает координатную плоскость на две полуплоскости. Выяснить, верно ли, что точки (a, b) и (c, d) принадлежат одной и той же полуплоскости.(**)
54 Даны действительные числа x1, x2, x3, y1, y2, y3. Принадлежит ли начало координат треугольнику с вершинами (x1, y1), (x2, y2), (x3, y3)?
55 Даны действительные положительные числа a, b, c, d. Выяснить можно ли прямоугольник со сторонами a, b уместить внутри прямоугольника со сторонами c, d так, чтобы каждая из сторон одного прчмоугольника была параллельна или перпендикулярна каждой стороне второго прямоугольника.
56 Даны действительные положительные числа a, b, c, x, y. Выяснить, пройдет ли кирпич с ребрами a, b, c в прямоугольное отверстие со сторонами x, y. Просовывать кирпич в отверстие разрешается только так, чтобы каждое из его ребер было параллельно или перпендикулярно каждой из сторон отверстия.
57 Дано действительное число a. Вычислить f(a), если
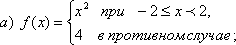
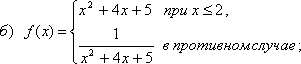
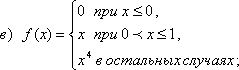
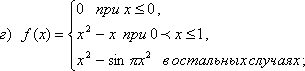
58 Дано действительное число a. Для функции f(x), графики которых представланы на рис.1 а - г, вычислить f(a).
59 Даны действительные числа x, y. Определить, принадлежит ли точка с координатами x, y заштрихованной части плоскости
(рис.2, а - к).
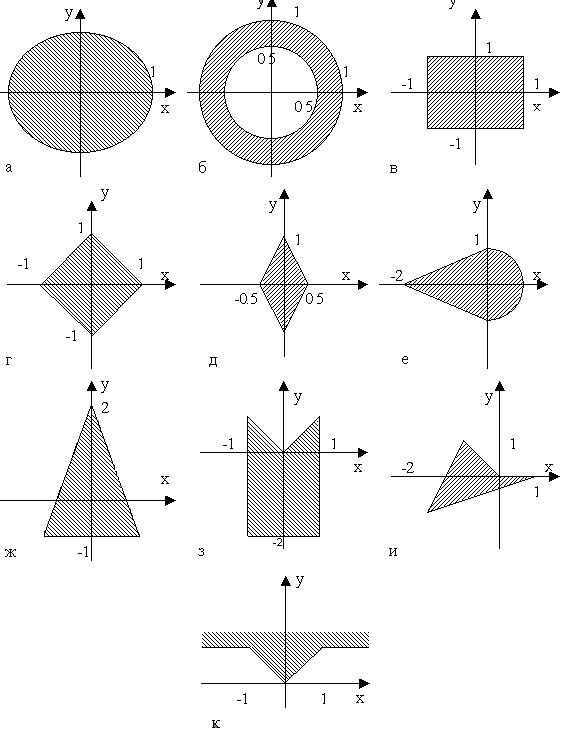
Рис.2
60 Пусть D - заштрихованная часть плоскости (рис.3, а - е) и пусть U определяется по x и y следующим
образом (запись(x, y)Є D означает, что точка с координатами x, y принадлежит D):
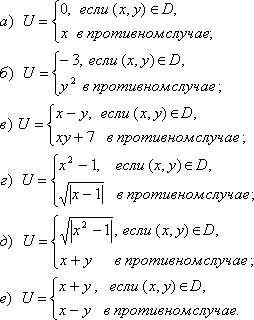
- Даны действительные числа x, y. Определить U.

(*) В этой задаче, как и вряде следующих задач, надо воспользоваться тем, что две точки (a, b) и (c, d), не лежащие на прямой, определяемой уравнением sx + ty + u = 0, принадлежат одной полуплоскости, если sa + tb + u и sc + td + u - числа одного знака. Справедлив и более общий факт: если уравнение F(x, y) = 0 определяет прямую или кривую, разбивающую координатную плоскость на две части, то точки (a, b) и (c, d), не лежащие на этой линии, принадлежат одной и той же части плоскости, если F(a, b) и F(c, d) - числа одного знака.
(**) В этой задаче, как и в ряде следующих задач, надо воспользоваться тем, что уравнением прямой, проходящей через две различные точки (e, f) и (g, h), является уравнение (x - e)(h - f) - (y - f)(g - e) = 0.
 Предыдущая глава
Предыдущая глава