77 Дано натуральное число n. Вычислить:
78 Даны действительное число а, натуральное число n. Вычислить:
79 Вычислить (1 + sin0.1)(1 + sin0.2)...(1 + sin10).
80 Дано действительное число х. Вычислить
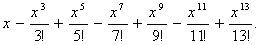
81 Даны действительные числа х, а, натуральное число n.
Вычислить
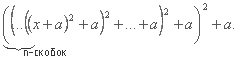
82 Дано действительное число х. Вычислить
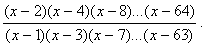
83 Дано действительное число а. Найти:
84 Даны натуральное n, действительное х. Вычислить:
85 Даны действительные числа a, h, натуральное число n. Вычислить
f(a) + 2f(a + h) + 2f(a + 2h) + ... + 2f(а + (n-1)h) + f(a + nh), где f (х) = (х2 + 1) cos2 x.
86 Дано натуральное число n.
87 Даны натуральные числа n, m. Получить сумму m последних цифр числа n.
88 Дано натуральное число n.
89 Алгоритм Евклида нахождения наибольшего общего делителя (НОД) неотрицательных целых чисел основан на следующих свойствах этой величины. Пусть т и n — одно временно не равные нулю целые неотрицательные числа и пусть m≥n. Тогда, если n = 0, то НОД (n, т) = т, а если n≠0, то для чисел m, n и r, где r—остаток от деления m на n, выполняется равенство НОД (m, n) = НОД(n, r). Например, НОД(15, 6) = НОД(6, 3) = НОД(3, 0) = 3. Даны натуральные числа n, m.
90 Даны натуральные числа т и n. Найти такие натуральные р и q, не имеющие общих делителей, что
p/q = m/n.
91 Пусть ao=1; ak =kak-1+1/k, k=1, 2, ... Дано натуральное число n. Получить аn.
92 Пусть v1 = v2 = 0; v 3 = 1.5;
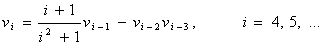
93 Пусть xo= c; x1= d; xk= qxk-1 + rxk-2+b, k = 2, 3, ...
94 Пусть u1= u2 = 0; v1 = v2 = 1;
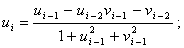
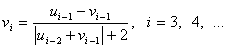
95 Пусть ao= a1= 1, ai = ai-2+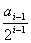 ,
,
96 Пусть a1=b1=1;
97 Пусть x1 = y1=l; xi= 0.3xi-1;
yi=xi-1+yi-1, i = 2, 3, ...
Дано натуральное n. Найти
98 Пусть a1=b1 =1; ak=3bk-1+2a k-1;
bk=2ak-1+bk-1, k = 2, 3, ...
99 Пусть a1 =u; b1 = v; ak = 2b k-1+ak-1;
bk= 2ak-12+bk-1, k = 2, 3, ...
100 Пусть x1 = х2 = х3= 1; xi=xi-1+xi-3, i = 4,5,...Найти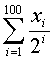
101 Даны положительные действительные числа a, x,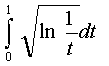 .
В последовательности y1, y2, ..., образованной по закону
.
В последовательности y1, y2, ..., образованной по закону
y0 = a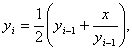 i = 1, 2, ...
i = 1, 2, ...
найти первый член yn, для которого выполнено неравенство |yn2 - y2n-1| < ε
102 Пусть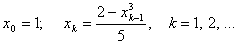 Найти первый член Xn,
для которого |xn - xn-1| < 10-5
Найти первый член Xn,
для которого |xn - xn-1| < 10-5
103 Пусть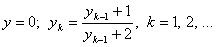
Дано действительное ε < 0. Найти первый член yn, для которого выполнено yn - yn-1 < ε
104 Дано действительное a > 0. Последовательность X0, X1, ... образована по закону
105 Даны натуральное число n, действительное число x. Вычислить:
106 Даны действительные числа a, b, натуральное число n (b>a). Получить (f1+...+fn)h, где
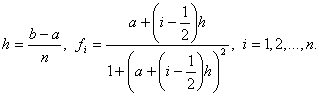
107 Дано натуральное число m>1. Получить наибольшее целое k, при котором 4k < m.
108 Дано натуральное число n. Получить наименьшее число вида 2r, превосходящее n.
109 Дано натуральное число n. Вычислить: 1*2+2*3*4+...+n*(n+1)*...*2n.
110 Вычислить:
111 Дано действительное число x № 0. Вычислить
112 Даны целые числа n, k (n ≥ k ≥ 0). Вычислить
113 Пусть n - натуральное число и пусть n!!означает 1*3*5*...*n для нечетного n и 2*4*....*n для чётного n. Для заданного натурального n вычислить:
114 Вычислить:
115 Дано натуральное число n. Вычислить:
116 Даны натурально число n, действительное число x. Вычислить:
117 Дано натуральное число n. Вычислить произведение первых n сомножителей:
118 Вычислить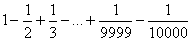 следующими способами:
следующими способами:
119 Вычислить бесконечную сумму с заданной точностью ε (ε > 0). Считать, что требуемая точность достигнута, если вычислена сумма нескольких первых слагаемых и очередное слогаемое оказалось по модулю меньше, чем ε, - это и все последующие слагаемые можно уже не учитывать. Вычислить:
-
a) 2n;
б) n!;
в)
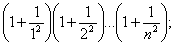
г)
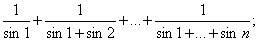
д)
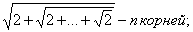
е)
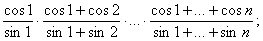
ж)
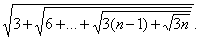
78 Даны действительное число а, натуральное число n. Вычислить:
-
а) аn;
б) а(а + 1)...(a + n - 1);
в)
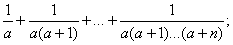
г)
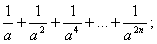
д) а(а — n)(а — 2n)...(а — n2).
79 Вычислить (1 + sin0.1)(1 + sin0.2)...(1 + sin10).
80 Дано действительное число х. Вычислить
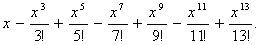
81 Даны действительные числа х, а, натуральное число n.
Вычислить
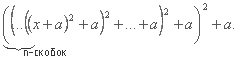
82 Дано действительное число х. Вычислить
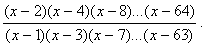
83 Дано действительное число а. Найти:
-
а) среди чисел 1, 1+1/2, 1+1/2+1/3,...
первое, большее а;
б) такое наименьшее n, что 1+1/2+ ... +1/n> а.
84 Даны натуральное n, действительное х. Вычислить:
-
а) sin х + sin2 х + ... + sinn х;
б) sin х + sin x2 + ... + sin xn;
в) sin х + sin sin x + ... + sin sin ...sin x;
85 Даны действительные числа a, h, натуральное число n. Вычислить
f(a) + 2f(a + h) + 2f(a + 2h) + ... + 2f(а + (n-1)h) + f(a + nh), где f (х) = (х2 + 1) cos2 x.
86 Дано натуральное число n.
-
а) Сколько цифр в числе n?
б) Чему равна сумма его цифр?
в) Найти первую цифру числа n.
г) Найти знакочередующуюся сумму цифр числа n (пусть запись n в десятичной системе есть
аk, аk-1. . . aо; найти аk - ak-1+ ...+(-1)kaо).
87 Даны натуральные числа n, m. Получить сумму m последних цифр числа n.
88 Дано натуральное число n.
-
а) Выяснить, входит ли цифра 3 в запись числа n2.
б) Поменять порядок цифр числа n на обратный.
в) Переставить первую и последнюю цифры числа n.
г) Приписать по единице в начало и в конец записи числа n.
89 Алгоритм Евклида нахождения наибольшего общего делителя (НОД) неотрицательных целых чисел основан на следующих свойствах этой величины. Пусть т и n — одно временно не равные нулю целые неотрицательные числа и пусть m≥n. Тогда, если n = 0, то НОД (n, т) = т, а если n≠0, то для чисел m, n и r, где r—остаток от деления m на n, выполняется равенство НОД (m, n) = НОД(n, r). Например, НОД(15, 6) = НОД(6, 3) = НОД(3, 0) = 3. Даны натуральные числа n, m.
-
а) Используя алгоритм Евклида, найти наибольший общий делитель n и m.
б) Найти наименьшее общее кратное n и m. (Как здесь может помочь алгоритм Евклида?)
90 Даны натуральные числа т и n. Найти такие натуральные р и q, не имеющие общих делителей, что
p/q = m/n.
91 Пусть ao=1; ak =kak-1+1/k, k=1, 2, ... Дано натуральное число n. Получить аn.
92 Пусть v1 = v2 = 0; v 3 = 1.5;
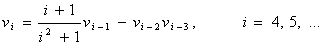
- Дано натуральное число n (n >= 4) получить
v n.
93 Пусть xo= c; x1= d; xk= qxk-1 + rxk-2+b, k = 2, 3, ...
- Даны действительные q, r, b, с, d, натуральное n (n>=2).
Получить хn.
94 Пусть u1= u2 = 0; v1 = v2 = 1;
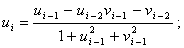
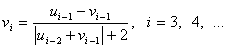
- Дано натуральное число n
(n >= 3) получить v n.
95 Пусть ao= a1= 1, ai = ai-2+
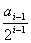 ,
,- Найти произведение аo* a1* ... *
а14.
96 Пусть a1=b1=1;
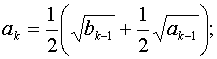
bk = 2a2k-1 + bk-1, k = 2, 3, ....
- Дано натуральное n найти
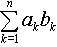 (*)
(*)
97 Пусть x1 = y1=l; xi= 0.3xi-1;
yi=xi-1+yi-1, i = 2, 3, ...
Дано натуральное n. Найти
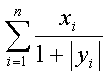
98 Пусть a1=b1 =1; ak=3bk-1+2a k-1;
bk=2ak-1+bk-1, k = 2, 3, ...
- Дано натуральное n. Найти
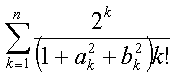
99 Пусть a1 =u; b1 = v; ak = 2b k-1+ak-1;
bk= 2ak-12+bk-1, k = 2, 3, ...
- Даны действительные u, v, натуральное n. Найти
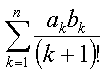
100 Пусть x1 = х2 = х3= 1; xi=xi-1+xi-3, i = 4,5,...Найти
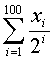
101 Даны положительные действительные числа a, x,
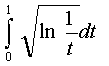 .
В последовательности y1, y2, ..., образованной по закону
.
В последовательности y1, y2, ..., образованной по закону y0 = a
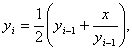 i = 1, 2, ...
i = 1, 2, ...найти первый член yn, для которого выполнено неравенство |yn2 - y2n-1| < ε
102 Пусть
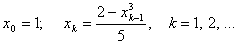 Найти первый член Xn,
для которого |xn - xn-1| < 10-5
Найти первый член Xn,
для которого |xn - xn-1| < 10-5103 Пусть
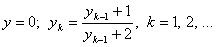
Дано действительное ε < 0. Найти первый член yn, для которого выполнено yn - yn-1 < ε
104 Дано действительное a > 0. Последовательность X0, X1, ... образована по закону
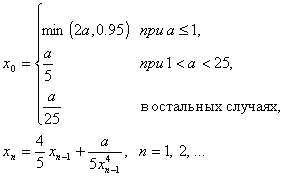
- Найти первый член xn, для которого
(5/4)a|xn+1 - xn| < 10-6
- Вычислить для найденного хn
разность a - x n5.
105 Даны натуральное число n, действительное число x. Вычислить:
-
а) xn2/2n;
б) xn3/3n
106 Даны действительные числа a, b, натуральное число n (b>a). Получить (f1+...+fn)h, где
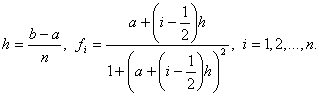
107 Дано натуральное число m>1. Получить наибольшее целое k, при котором 4k < m.
108 Дано натуральное число n. Получить наименьшее число вида 2r, превосходящее n.
109 Дано натуральное число n. Вычислить: 1*2+2*3*4+...+n*(n+1)*...*2n.
110 Вычислить:
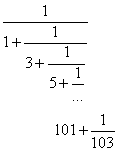
111 Дано действительное число x № 0. Вычислить
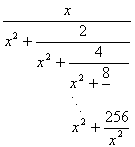
112 Даны целые числа n, k (n ≥ k ≥ 0). Вычислить
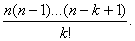
113 Пусть n - натуральное число и пусть n!!означает 1*3*5*...*n для нечетного n и 2*4*....*n для чётного n. Для заданного натурального n вычислить:
-
а) n!!
б) (-1)n+1n!!
114 Вычислить:
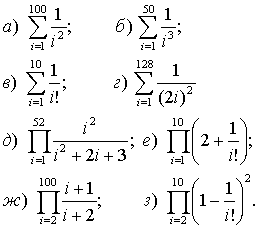
115 Дано натуральное число n. Вычислить:
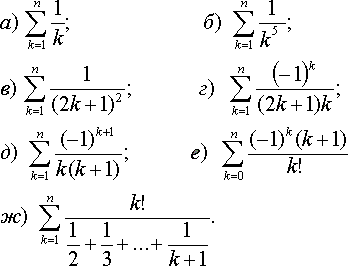
116 Даны натурально число n, действительное число x. Вычислить:
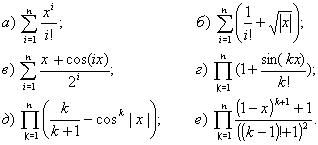
117 Дано натуральное число n. Вычислить произведение первых n сомножителей:
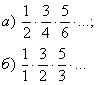
118 Вычислить
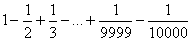 следующими способами:
следующими способами:-
а) последовательно с лева на право;
б) последовательно с лева на право вычисляются
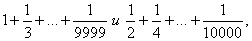 , затем второе
значение вычисляется из первого;
, затем второе
значение вычисляется из первого;в) последовательно с права на лево;
г) последовательно с права на лево, вычисляются суммы выписанные в б), затем - вычитание.
- Почему при вычислениях на вычислительной машине каждым из этих способов получаются разные результаты?
119 Вычислить бесконечную сумму с заданной точностью ε (ε > 0). Считать, что требуемая точность достигнута, если вычислена сумма нескольких первых слагаемых и очередное слогаемое оказалось по модулю меньше, чем ε, - это и все последующие слагаемые можно уже не учитывать. Вычислить:
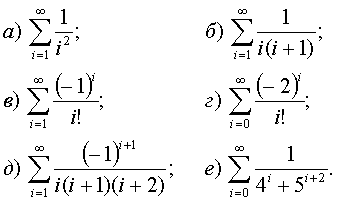
 Предыдущая глава
Предыдущая глава