136 Даны натуральное число n, действительные числа a1,...,
an. Вычислить:
137 Даны натуральное число n, действительные числа а1,..., an. Вычислить:
138 Даны действительные числа а1, ..., a70. Получить (вывести) последовательность а 2, а 3, ..., a70, a1.
139 Дано натуральное число n. Получить последовательность b1, ..., bn, где при i = 1, 2, ..., n значение b i равно:
140 Вычислить значения выражения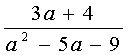 для
а = 1, 2, ..., 100.
для
а = 1, 2, ..., 100.
141 Цилиндр объема единица имеет высоту h. Определить радиус основания цилиндра для значений h, равных 0.5, 1, 1.5, ..., 5.
142 Вычислить значения многочлена x5 - 9x4 + 1.7x2 - 9.6 для x = 0, 1, ..., 5.
143 Даны действительные числа a1, a2, a3, a4, x1, ..., x50. Получить b1, ..., b50, где
144 Последовательность чисел Фибоначчи u0, u1, ...образуется по закону u0 = 0; u1 = 1; ui = ui-1 + ui-2 (i = 2, 3, ...).
145 Последовательность x1, x2, ...образована по закону:
146 Даны натуральное число n, действительные числа a,b (a ≠ b). Получить r0, r1, ..., rn, где ri = a + ih, h = (b - a)/n.
147 Вычислить последовательности значений функций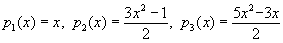 для значений аргумента x = 0, 0.05, 0.1, ..., 20.
для значений аргумента x = 0, 0.05, 0.1, ..., 20.
148 Получить таблицу температур по Цельсию от 0 до 100 градусов и их эквивалентов по шкале Фаренгейта, используя для перевода формулу tF = (9/5)tc + 32.
149 Вычислить значения функции y = 4x3 - 2x2 + 5 для значений x, изменяющихся от -3 до 1, с шагом 0,1.
150 Дано натуральное число n. Вычислить значения функции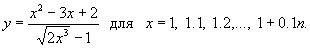
151 Дано натуральное число n, действительные положительные числа C1, ..., Cn. Значения C1, ..., Cn являются емкостями n конденсаторов. Определить емкости систем конденсаторов, которые получаются последовательным и параллельным соединением исходных конденсаторов.
152 Даны натуральное число n, действительные числа a, h, b, d0,..., dn.Вычислить
153 Даны натуральное число n, действительные числа x, an, an-1, ..., a0. Вычислить, используя схему Горнера(**), значение anxn + an-1xn-1 + ... + a0.
154 Дано натуральное число n,действительные числа a, b, x1 y1,..., xn, yn. Пара a, b - координаты школы микрорайона, а пара xi, yi(i = 1, ..., n) - соответственно координаты домов этого микрорайона. Найти расстояния от домов до школы и среднее арифметическое этих расстояний.
155 Даны натуральное число n, действительные числа x1,...xn (n ≥ 2).Вычислить
156 Даны натуральное число n, действительные числа x1,...xn (n ≥ 3). Вычислить:
157 Даны натуральное число n, действительные числа a, b, (b > a > 0). Получить последовательность действительных числел y0, y1, ..., yn, где yi = √ xi, xi = a + ih, h = (b - a)/n.
158 Даны натуральное число n, целые числа a1,..., a39. В последовательности a1,..., a39 заменить каждый из членов остатком от деления его квадрата на n.
159 Даны натуральное число n, действительные числа a1,..., an (n ≥ 3). Получить b1,..., bn-2, где bi = ai + 1 + ai+2, i = 1,..., n-2.
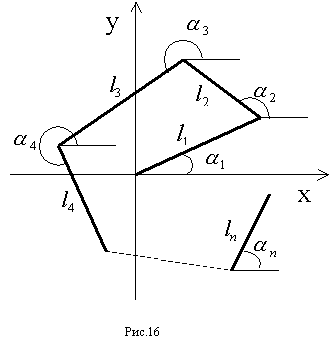
160 Даны натуральное число n, действительные числа α1, l1, α2, l2, ..., αn, ln (l1, l2, ..., ln ≥ 0). Найти координаты конца ломаной линии, изображенной на рис. 16.
161 Даны натуральное число n, действительные числа a1,..., an. Получить b1,..., bn, где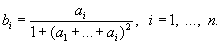
162 Даны натуральное число i, n, действительные числа a1,..., an (i ≤ n). Найти среднее арифметическое всех чисел a1,..., an кроме ai.
163 Даны действительные числа a1,..., a37. Все члены этой последовательности, начиная с первого положительного, уменьшить на 0,5.
164 Даны действительные числа a1,..., a50. Получить "сглаженные" значения a1,..., a50, заменив в исходной последовательности все члены, кроме первого и последнего, по формуле
165 Даны действительные числа a1, a2,... Известно, что a1 > 0 и что среди a2, a3,... есть хотя бы одно отрицательное число. Пусть a1,..., an - члены данной последовательности, предшествующие первому отрицательному члену (n заранее неизвестно). Получить:
166 Даны натуральное число n, действительные числа a1,..., an. Получить числа b1,..., bn, которые связаны с a1,..., an следующим образом:
167 Пусть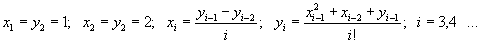 Получить:
Получить:
168 Даны натуральное число n, действиетльные чилса a1,..., an (n ≥ 6).
Получить:
169 Даны натуральные числа x, y1, ..., y100 (y1 < y2 < ... < y100, y1 < x ≤ y100). Найти натуральное k, при котором yk-1 < x ≤ yk.
170 Даны натуральные числа n, a1,..., an (n ≥ 4). Числа a1,..., an - это измеренные в сотых долях секунды результаты n спортсменов в беге на 100м. Составить команду из четырех лучших бегунов для участия в эстафете 4х100м , т.е. указать одну из четверок натуральных чисел i, j, k, l, для которой 1 ≤ i < j < k < l ≤ n и ai + aj + ak + al имеет наименьшее значение.
171 Даны натуральные числа n,a0,a1,a2,..., a3n-1. Каждая тройка чисел ai,ai+1,ai+2,где i кратно трем, задает координаты центра квадрата (ai,ai+1) и длину его стороны ai+2. Предполагается, что стороны квадратов расположены параллельно осям координат экрана. Построить и закрасиьт какими-либо цветами квадраты, заданные последовательностью a0,a1,a2,..., a3n-1.
172 Даны натуральные числа n,a0,a1,a2,..., a3n-1. Каждая тройка чисел ai,ai+1,ai+2,где i кратно трем, задает координаты центра круга (ai,ai+1) и его радиус ai+2. Построить и закрасиьт какими-либо цветами круги, заданные последовательностью a0, a1, a2, ..., a3n-1.
173 Даны натуральные числа n,a0,a1,a2,..., a4n-1. Каждая четыре числа ai,ai+1,ai+2,ai+3,где i кратно четырем, задают прямоугольник со сторонами, параллельными осям координат экрана: числа ai, ai+1 - это координаты центра прямоугольника, ai+2,ai+3 - длины его сторон. Построить и закрасиьт какими-либо цветами прямоугольники, заданные последовательностью a0, a1, a2, ..., a4n-1.
174 Даны натуральные числа n,a0,a1,a2,..., a6n-1. Каждая шесть чисел ai,ai+1,ai+2,ai+3,ai+4 ,ai+5,где i кратно шести, задают координаты вершин треугольника: числа ai,a i+1 - это координаты первой вершины, ai+2,ai+3 - координаты второй вершины, ai+4,ai+5 - координаты третьей вершины. Построить треугольники, заданные последовательностью a0,a1,a2,...,a6n-1.
175 Даны натуральные числа n,a0,a1,a2,..., a2n-1. Каждая пара чисел ai,ai+1,где i кратно двум, задает координаты вершин ломаной.
176 Даны натуральные числа n,a0,a1,a2,..., a3n-1. Каждая тройка чисел ai,ai+1,ai+2,где i кратно трем, задает координаты точки и ее цвет. Построить все точки, заданные последовательностью a0, a1,a2,...,a3n-1.
177 Даны натуральные числа n,x,y,r1,c1,r2, c2,...,rn,cn. Построить n концентрических окружностей с общим центром в точке (x, y),имеющих радиусы r1,...,rn и окрашенных в цвета с1, с2, ..., сn.
(*) - В задачах этого параграфа не требуется хранения исходных последовательностей значений.
(**) - anxn + an-1xn-1 + ... + ao = (... (anx + an-1)x + an-2)x + ... + a1)x + ao.
-
а) a1 + ... + an;
б) a1a2 ... an;
в) |a1| + ... + |an|;
г) |a1| ∙ |a2| ∙ ... ∙ |an|;
д) a12 + ... + an2;
е) a1 + ... + an и a1a2 ... an;
ж) a1 - a2 + a3 - ... + (-1)n+1an;
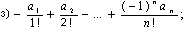
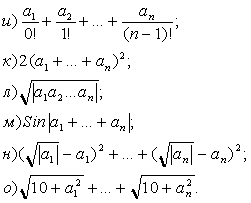
137 Даны натуральное число n, действительные числа а1,..., an. Вычислить:
-
а) a1, a1 + a2, ..., a1 + a2 + ...+ an;
б) a12, a1a2, a1a3, ..., a1an;
в) |a1|, |a1 + a2|, ..., |a1 + a2 + ...+ an|;
г) a1, - a1a2, a1a2a3, ..., (-1)n+1a1a2...an;
д) -a1, a2, -a3, ..., (-1)nan;
е) a1 + 1!, a2 + 2!, ..., an + n!.
138 Даны действительные числа а1, ..., a70. Получить (вывести) последовательность а 2, а 3, ..., a70, a1.
139 Дано натуральное число n. Получить последовательность b1, ..., bn, где при i = 1, 2, ..., n значение b i равно:
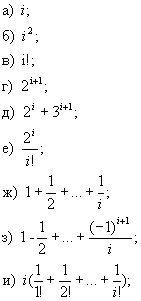
140 Вычислить значения выражения
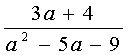 для
а = 1, 2, ..., 100.
для
а = 1, 2, ..., 100.141 Цилиндр объема единица имеет высоту h. Определить радиус основания цилиндра для значений h, равных 0.5, 1, 1.5, ..., 5.
142 Вычислить значения многочлена x5 - 9x4 + 1.7x2 - 9.6 для x = 0, 1, ..., 5.
143 Даны действительные числа a1, a2, a3, a4, x1, ..., x50. Получить b1, ..., b50, где
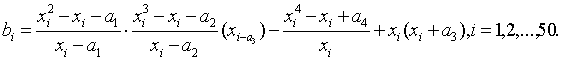
144 Последовательность чисел Фибоначчи u0, u1, ...образуется по закону u0 = 0; u1 = 1; ui = ui-1 + ui-2 (i = 2, 3, ...).
-
а) Дано натуральное число n > 1 Получить u0, u1, ..., un.
б) Последовательность f0, f1, ... образуется по закону f0 = 0; f1 = 1; fi = fi-1 + fi-2 + ui-2 (i = 2, 3, ...). Дано натуральное n > 1. Получить f0, f1, ..., fn.
145 Последовательность x1, x2, ...образована по закону:
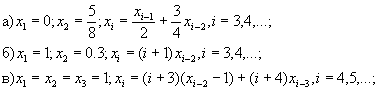
- Получить x1, x2, ..., x20.
146 Даны натуральное число n, действительные числа a,b (a ≠ b). Получить r0, r1, ..., rn, где ri = a + ih, h = (b - a)/n.
147 Вычислить последовательности значений функций
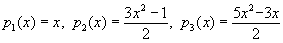 для значений аргумента x = 0, 0.05, 0.1, ..., 20.
для значений аргумента x = 0, 0.05, 0.1, ..., 20.148 Получить таблицу температур по Цельсию от 0 до 100 градусов и их эквивалентов по шкале Фаренгейта, используя для перевода формулу tF = (9/5)tc + 32.
149 Вычислить значения функции y = 4x3 - 2x2 + 5 для значений x, изменяющихся от -3 до 1, с шагом 0,1.
150 Дано натуральное число n. Вычислить значения функции
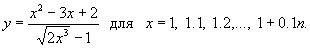
151 Дано натуральное число n, действительные положительные числа C1, ..., Cn. Значения C1, ..., Cn являются емкостями n конденсаторов. Определить емкости систем конденсаторов, которые получаются последовательным и параллельным соединением исходных конденсаторов.
152 Даны натуральное число n, действительные числа a, h, b, d0,..., dn.Вычислить
-
d0 + d1(b - a) + d2(b - a)(b- a - h) + ... + dn(b - a)
(b - a - h)...(b - a - (n - 1)h).
153 Даны натуральное число n, действительные числа x, an, an-1, ..., a0. Вычислить, используя схему Горнера(**), значение anxn + an-1xn-1 + ... + a0.
154 Дано натуральное число n,действительные числа a, b, x1 y1,..., xn, yn. Пара a, b - координаты школы микрорайона, а пара xi, yi(i = 1, ..., n) - соответственно координаты домов этого микрорайона. Найти расстояния от домов до школы и среднее арифметическое этих расстояний.
155 Даны натуральное число n, действительные числа x1,...xn (n ≥ 2).Вычислить
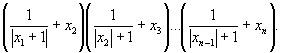
156 Даны натуральное число n, действительные числа x1,...xn (n ≥ 3). Вычислить:
-
а) (x1 +2x2 + x3)(x2 + 2x3 + x4) ...
(xn-2 + 2xn-1 + xn);
б) (x1 +x2 + x3)x2 + (x2 + x3 + x4)x3 + ... + (xn-2 + xn-1 + xn)xn-1.
157 Даны натуральное число n, действительные числа a, b, (b > a > 0). Получить последовательность действительных числел y0, y1, ..., yn, где yi = √ xi, xi = a + ih, h = (b - a)/n.
158 Даны натуральное число n, целые числа a1,..., a39. В последовательности a1,..., a39 заменить каждый из членов остатком от деления его квадрата на n.
159 Даны натуральное число n, действительные числа a1,..., an (n ≥ 3). Получить b1,..., bn-2, где bi = ai + 1 + ai+2, i = 1,..., n-2.
160 Даны натуральное число n, действительные числа α1, l1, α2, l2, ..., αn, ln (l1, l2, ..., ln ≥ 0). Найти координаты конца ломаной линии, изображенной на рис. 16.

161 Даны натуральное число n, действительные числа a1,..., an. Получить b1,..., bn, где
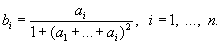
162 Даны натуральное число i, n, действительные числа a1,..., an (i ≤ n). Найти среднее арифметическое всех чисел a1,..., an кроме ai.
163 Даны действительные числа a1,..., a37. Все члены этой последовательности, начиная с первого положительного, уменьшить на 0,5.
164 Даны действительные числа a1,..., a50. Получить "сглаженные" значения a1,..., a50, заменив в исходной последовательности все члены, кроме первого и последнего, по формуле
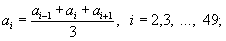
- считается, что
-
а) после того как получено новое значение некоторого члена, оно используется для вычисления нового
значения следующего члена;
б) при "сглаживании" используются лишь старые значения членов.
165 Даны действительные числа a1, a2,... Известно, что a1 > 0 и что среди a2, a3,... есть хотя бы одно отрицательное число. Пусть a1,..., an - члены данной последовательности, предшествующие первому отрицательному члену (n заранее неизвестно). Получить:
-
а) a1 + a2 + ... + an;
б) a1a2...an;
в) среднее арифметическое a1, ..., an;
г) среднее геометрическое a1, ..., an;
д) a1, a1a2, a1a2a3, ..., a1a2...an;
е) a1 + 2a2 + 2a3 + ... + 2an-1 + an;
ж) a1a2 + a2a3 + ... + an-1an + ana1;
з) (-1)nan;
и) n + an;
к) |a1 - an|.
166 Даны натуральное число n, действительные числа a1,..., an. Получить числа b1,..., bn, которые связаны с a1,..., an следующим образом:
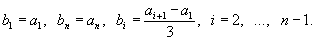
167 Пусть
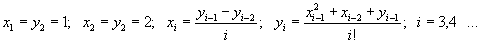 Получить:
Получить:
-
а) x1, y1, x2, y2, ..., x25, y25;
б) y1/2, y2/3, ..., y25/26.
168 Даны натуральное число n, действиетльные чилса a1,..., an (n ≥ 6).
Получить:
-
а) a6, a7, ..., an;
б) a6, a7, ..., an, a1;
в) a6, a7, ..., an, a5.
169 Даны натуральные числа x, y1, ..., y100 (y1 < y2 < ... < y100, y1 < x ≤ y100). Найти натуральное k, при котором yk-1 < x ≤ yk.
170 Даны натуральные числа n, a1,..., an (n ≥ 4). Числа a1,..., an - это измеренные в сотых долях секунды результаты n спортсменов в беге на 100м. Составить команду из четырех лучших бегунов для участия в эстафете 4х100м , т.е. указать одну из четверок натуральных чисел i, j, k, l, для которой 1 ≤ i < j < k < l ≤ n и ai + aj + ak + al имеет наименьшее значение.
171 Даны натуральные числа n,a0,a1,a2,..., a3n-1. Каждая тройка чисел ai,ai+1,ai+2,где i кратно трем, задает координаты центра квадрата (ai,ai+1) и длину его стороны ai+2. Предполагается, что стороны квадратов расположены параллельно осям координат экрана. Построить и закрасиьт какими-либо цветами квадраты, заданные последовательностью a0,a1,a2,..., a3n-1.
172 Даны натуральные числа n,a0,a1,a2,..., a3n-1. Каждая тройка чисел ai,ai+1,ai+2,где i кратно трем, задает координаты центра круга (ai,ai+1) и его радиус ai+2. Построить и закрасиьт какими-либо цветами круги, заданные последовательностью a0, a1, a2, ..., a3n-1.
173 Даны натуральные числа n,a0,a1,a2,..., a4n-1. Каждая четыре числа ai,ai+1,ai+2,ai+3,где i кратно четырем, задают прямоугольник со сторонами, параллельными осям координат экрана: числа ai, ai+1 - это координаты центра прямоугольника, ai+2,ai+3 - длины его сторон. Построить и закрасиьт какими-либо цветами прямоугольники, заданные последовательностью a0, a1, a2, ..., a4n-1.
174 Даны натуральные числа n,a0,a1,a2,..., a6n-1. Каждая шесть чисел ai,ai+1,ai+2,ai+3,ai+4 ,ai+5,где i кратно шести, задают координаты вершин треугольника: числа ai,a i+1 - это координаты первой вершины, ai+2,ai+3 - координаты второй вершины, ai+4,ai+5 - координаты третьей вершины. Построить треугольники, заданные последовательностью a0,a1,a2,...,a6n-1.
175 Даны натуральные числа n,a0,a1,a2,..., a2n-1. Каждая пара чисел ai,ai+1,где i кратно двум, задает координаты вершин ломаной.
-
а) Построить ломаную, заданную последовательностью a0,a1,a2,...,
a2n-1.
б) Построить ломаную, заданную последовательностью a0,a1,a2,..., a2n-1; последнюю вершину соединить с первой.
176 Даны натуральные числа n,a0,a1,a2,..., a3n-1. Каждая тройка чисел ai,ai+1,ai+2,где i кратно трем, задает координаты точки и ее цвет. Построить все точки, заданные последовательностью a0, a1,a2,...,a3n-1.
177 Даны натуральные числа n,x,y,r1,c1,r2, c2,...,rn,cn. Построить n концентрических окружностей с общим центром в точке (x, y),имеющих радиусы r1,...,rn и окрашенных в цвета с1, с2, ..., сn.
(*) - В задачах этого параграфа не требуется хранения исходных последовательностей значений.
(**) - anxn + an-1xn-1 + ... + ao = (... (anx + an-1)x + an-2)x + ... + a1)x + ao.
 Предыдущая глава
Предыдущая глава