531 Даны натуральное число n, деиствительные числа x1, ..., xn
(n ≥ 2). Получить последовательность x1 - xn, x2 - xn...,
xn-1 - xn.
532 Даны натуральное число n, действительные числа а1..., аn. Если последовательность а1, ..., аn упорядочена по неубыванию (т.е.если а1≤ а2≤...≤ аn, то оставить ее без изменения. Иначе получить последовательность аn, ..., а1.

534 Даны натуральное число n, действительные числа a1, ..., a2n. Получить
535 Пусть a1 = 1; a2 = 1.5; ai = a[i/2]a[i/3] + 1 ( i = 3, 4...). Дано натуральное число m. Получить am.
536 Даны натуральное число n, целые числа a1, ..., an. Выяснить имеются ли среди чисел a1, ..., anсовпадающие.
537 Даны натуральное число n, целые числа a1, ..., an. Выяснить, верно ли, что для всех a2n+1, ..., a3n имеются равные среди a1, ..., a2n.
538 Даны натуральное число n, действительные числа r1, ..., rn. Получить последовательность:
539 Даны натуральное число n, действительные числа a1, ..., an. Требуется получить последовательность x1, y1, x2, y2, ..., xk, yk, где x1..., xm-взятые в порядке следования четные члены последовательности a1, ..., an1, ..., yl - нечетные члены, k = min(m, l).
540 Даны натуральное число n, действительные числа a1, ..., a2n. Выяснить, верно ли, что для i = 1, ..., n выполнено:
541 Даны натуральное число n, действительные числа a1, ..., an. Преобразовать последовательность a1, ..., an, расположив вначале отрицательные члены, а затем - неотрицательные. При этом:
542 Даны натуральное число n, действительные числа a1, ..., an. Вычислить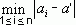 , где a`-cреднее арифметическое чисел a1, ...,
an.
, где a`-cреднее арифметическое чисел a1, ...,
an.
543 Даны натуральное число n, действительные числа x1, ..., xn, p1, ..., pn. Последовательности x1, ..., xn и p1, ..., pn определяют систему n материальных точек на прямой: xi-координата, pi-вес i-й точки ( i = 1, ..., n). Указать номер точки, наиболее близко расположенной к центру тяжести системы. Если таких точек несколько, то взять любую из них.
544 Даны натуральное число n, действительные числа a1, ..., an. Eсли в последовательности a1, ..., an есть хотя бы один член, меньший, чем-3, то все отрицательные члены заменить их квадратами, в противном случае домножить все члены на 0, 1.
545 Даны натуральные n, m. Предпологается, что n человек встают в круг и получают номера, считая против часовой стрелки, 1, 2, ..., n. Затем, начиная c первого, также против часовой стрелки отсчитывается m-й человек (поскольку люди стоят по кругу, то за n-м человеком стоит первый ). Этот человек выходит из круга, после чего, начиная со следующего, снова отсчитывается m-й человек и так до тех пор, пока из всего круга не останется один человек. Определить его номер. Для решения этой задачи полезен список, соединяющий в кольцо так, как показано на рис. 28.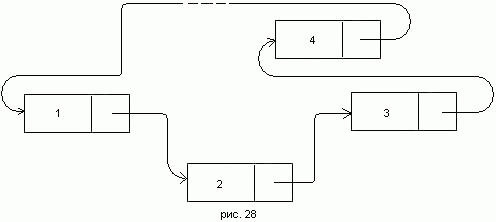
546 Даны натуральные n, m, символы s1, ..., sn (m < n). Получить последовательность символов:
547 Даны натуральное число n, символы s1, ..., sn. Известно что в последовательность s1, ..., sm входит по крайней мере один пробел. Пусть m таково , что sm - это первый по порядку пробел, входящий в s1, ..., sn(m зарание неизвестно). Выполнить преобразования а), б) , в) сформулированные в предыдущей задаче.
548 Даны натуральное число n, символы s1, ..., sn. Получчить те символы, принадлежащие последовательности s1, ..., sn, которые входят в эту последовательность по одному разу.
549 Даны натуральное число n, символы s1, ..., sn. Получить последовательность символов, содержащую только последние вхождения каждого символа с сохранением взаимного порядка этих вхождений.
550 Даны натуральные числа k, m, n, символы s1, ..., sk, t1, ..., tm, u1, ..., un. Получить по одному разу те символы, которые входят одновременно во все три последовательности.
551 Даны натуральное число n, символы s1, ..., sn. Будем рассматривать слова, образованные входящими в последовательность s1, ..., snсимволами (см.задачу 269). Ниже описываются преобразования, каждое из которых следует произвести при выполнении указаного условия. Затем последовательность вне зависимости от того, подвергалась она или нет преобразованию, должна быть отредактирована следующим образом. Должны быть удалены группы пробелов, которыми начинается и заканчивается последовательность, а каждая внутренняя группа пробелов должна быть заменена одним пробелом. Преобразования:
552 Даны символы s1, s2, ... Известно, что символ s1 отличен от точки и что среди s2, ..., s3, ... иеется хотя бы одна точка. Пусть s1, ..., sn - cимволы, предшествующие первой точке (n зарание неизвестно). Получить
553 Если требуется хранение последовательности, число членов которой ограничено сверху некоторым известным числом N, то можно использовать для хранения последовательности массив с N элементами, занимая, таким образом, память вычислительной машины с некоторым запасом.Это позволяет обойтись без списков.
- Для решения этой задачи полезен список, изображенный на рисунке
25.

532 Даны натуральное число n, действительные числа а1..., аn. Если последовательность а1, ..., аn упорядочена по неубыванию (т.е.если а1≤ а2≤...≤ аn, то оставить ее без изменения. Иначе получить последовательность аn, ..., а1.
- Для решения этой задачи полезен список,
изображенный на рис. 26.

-
а) x1xn + x2xn-1 +...+ xnx1;
б) (x1 + xn)(x2 + xn-1)...(xn + x1);
в) (x1 + x2 + 2xn)(x2 + x3 + 2xx-1)... (xn-1 + xn + 2x2).
- Для решения этой задачи полезен список, изображенный на рис. 27.

534 Даны натуральное число n, действительные числа a1, ..., a2n. Получить
-
а) (a1-a2n)(a3-a2n-2)(a5-a2n-4)...
(a2n-1-a2);
б) a1a2n + a2a2n-1 +...+ anan+1;
в) min(a1 + an+1, a2 + an+2, ..., an + a2n);
г) max(min(a1, a2n), min(a2, a2n-1), min(an) + a2n)).
535 Пусть a1 = 1; a2 = 1.5; ai = a[i/2]a[i/3] + 1 ( i = 3, 4...). Дано натуральное число m. Получить am.
536 Даны натуральное число n, целые числа a1, ..., an. Выяснить имеются ли среди чисел a1, ..., anсовпадающие.
537 Даны натуральное число n, целые числа a1, ..., an. Выяснить, верно ли, что для всех a2n+1, ..., a3n имеются равные среди a1, ..., a2n.
538 Даны натуральное число n, действительные числа r1, ..., rn. Получить последовательность:
-
а) r1, ..., rn, r1..., rn;
б) r1, ..., rn, rn..., r1;
в) rn, ..., r1, r1..., rn;
539 Даны натуральное число n, действительные числа a1, ..., an. Требуется получить последовательность x1, y1, x2, y2, ..., xk, yk, где x1..., xm-взятые в порядке следования четные члены последовательности a1, ..., an1, ..., yl - нечетные члены, k = min(m, l).
540 Даны натуральное число n, действительные числа a1, ..., a2n. Выяснить, верно ли, что для i = 1, ..., n выполнено:
-
а) ai = -ay+i;
б) ai = 2an-i + a2n-i + 1;
в) ai + a2n-i + 1>17;
г) a2n-i+1
541 Даны натуральное число n, действительные числа a1, ..., an. Преобразовать последовательность a1, ..., an, расположив вначале отрицательные члены, а затем - неотрицательные. При этом:
-
а) порядок как отрицательных, так и неотрицательных чисел сохраняется прежним;
б) порядок отрицательных чисел изменяется на обратный, а порядок неотрицательных сохраняется прежним;
в) порядок отрицательных чисел сохраняется прежним, a порядок неотрицательных изменяется на обратный;
г) порядок тех и других чисел изменяется на обратный.
542 Даны натуральное число n, действительные числа a1, ..., an. Вычислить
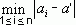 , где a`-cреднее арифметическое чисел a1, ...,
an.
, где a`-cреднее арифметическое чисел a1, ...,
an.543 Даны натуральное число n, действительные числа x1, ..., xn, p1, ..., pn. Последовательности x1, ..., xn и p1, ..., pn определяют систему n материальных точек на прямой: xi-координата, pi-вес i-й точки ( i = 1, ..., n). Указать номер точки, наиболее близко расположенной к центру тяжести системы. Если таких точек несколько, то взять любую из них.
544 Даны натуральное число n, действительные числа a1, ..., an. Eсли в последовательности a1, ..., an есть хотя бы один член, меньший, чем-3, то все отрицательные члены заменить их квадратами, в противном случае домножить все члены на 0, 1.
545 Даны натуральные n, m. Предпологается, что n человек встают в круг и получают номера, считая против часовой стрелки, 1, 2, ..., n. Затем, начиная c первого, также против часовой стрелки отсчитывается m-й человек (поскольку люди стоят по кругу, то за n-м человеком стоит первый ). Этот человек выходит из круга, после чего, начиная со следующего, снова отсчитывается m-й человек и так до тех пор, пока из всего круга не останется один человек. Определить его номер. Для решения этой задачи полезен список, соединяющий в кольцо так, как показано на рис. 28.

546 Даны натуральные n, m, символы s1, ..., sn (m < n). Получить последовательность символов:
-
а) sm+1, sm+2, ..., s1, ..., sm;
б) sm+1, sm+2, ..., sm, ..., s1;
в) sn, ..., sn-1, ..., sm+1, ..., s1, ..., sm
547 Даны натуральное число n, символы s1, ..., sn. Известно что в последовательность s1, ..., sm входит по крайней мере один пробел. Пусть m таково , что sm - это первый по порядку пробел, входящий в s1, ..., sn(m зарание неизвестно). Выполнить преобразования а), б) , в) сформулированные в предыдущей задаче.
548 Даны натуральное число n, символы s1, ..., sn. Получчить те символы, принадлежащие последовательности s1, ..., sn, которые входят в эту последовательность по одному разу.
549 Даны натуральное число n, символы s1, ..., sn. Получить последовательность символов, содержащую только последние вхождения каждого символа с сохранением взаимного порядка этих вхождений.
550 Даны натуральные числа k, m, n, символы s1, ..., sk, t1, ..., tm, u1, ..., un. Получить по одному разу те символы, которые входят одновременно во все три последовательности.
551 Даны натуральное число n, символы s1, ..., sn. Будем рассматривать слова, образованные входящими в последовательность s1, ..., snсимволами (см.задачу 269). Ниже описываются преобразования, каждое из которых следует произвести при выполнении указаного условия. Затем последовательность вне зависимости от того, подвергалась она или нет преобразованию, должна быть отредактирована следующим образом. Должны быть удалены группы пробелов, которыми начинается и заканчивается последовательность, а каждая внутренняя группа пробелов должна быть заменена одним пробелом. Преобразования:
-
а) если общее количество слов больше единици и нечетно, то удалить первое слово;
б) если последнее слово начинается с буквой а и общее число слов больще единицы, то переставить последнее слово в начало последовательности, отделив его пробелом от s1;
в) если первое и последнее слова совпадают и общее число слов больше единицы, то удалить первое и последнее слова, а оставшиеся символы переставить в обратном порядке.
552 Даны символы s1, s2, ... Известно, что символ s1 отличен от точки и что среди s2, ..., s3, ... иеется хотя бы одна точка. Пусть s1, ..., sn - cимволы, предшествующие первой точке (n зарание неизвестно). Получить
-
а) последовательность sn, sn-1, ..., s1;
б) последовательность s1, s3, ..., sn, если n-четное, и последовательность s2, s4, ..., sn, если n-четное.
553 Если требуется хранение последовательности, число членов которой ограничено сверху некоторым известным числом N, то можно использовать для хранения последовательности массив с N элементами, занимая, таким образом, память вычислительной машины с некоторым запасом.Это позволяет обойтись без списков.
-
а) Вернуться к задаче 531, cчитая, что n ≤ 1000.
б) Вернуться к задаче 532, считая, что n ≤ 1500.
в) Вернуться к задаче 550, считая, что k ≤ 1000, m ≤ 1000, l ≤ 100.
г) Вернуться к задаче 550, считая, что k + m + l ≤ 2000.
- Следует иметь в виду, что если используется несколько таких массивов, то суммарный излишек занятой памяти
может оказаться слишком большим для того, чтобы можно было воспользоваться этим приемом.
 Предыдущая глава
Предыдущая глава