606 Даны действительные положительные числа a, b, c, d.Выяснить, можно ли
построить четырехугольник с такими длинами сторон.
607 Дано действительное число φ (0 < φ < π). Из точки ( 1, 1 ) под углом φ к прямой x = 1 выпущен световой луч ( рис. 29, а - 29, б).
608 Даны действительные числа x1, y1, x2, y2 (x1≠x2 ), которые определяют две точки A(x1, y1) и B ( x2, y2 ). На оси абсцисс найти точку, сумма расстояний от которой до точек A и B - наименьшая для всех точек этой оси.
609 Даны действительные числа x, y. Вычислить расстояние от точки плоскости с координатами (x, y) до границы квадрата (т. е. минимум расстояний от данной точки до точек границы квадратов) с вершинами:
610 Даны натуральное число n, целые числа x1, y1, x2, y2, ..., xn, yn. Известно, что точки p1, ..., pn с координатами (x1, y1), (x2, y2), ..., (xn, yn) попарно различны. Пусть точка pi удалена от начала координат на расстояние ri ( i = 1, ..., n ). Пусть R = max ( r1, ..., rn ).
611 Даны действительные числа a1, ..., a50. Эти числа определяют 25 интервалов числовой оси: ( a1, a2), (a3, a4), ..., (a49, a50).
612 Даны действительные числа x1, ..., x15, y1, ..., y15, r1, ..., r15. Выяснить, есть ли на плоскости точка, принадлежащая всем кругам c1, ..., c15, где ci имеет центр с координатами xi, yi и радиус ri( i = 1, ..., 15 ).
613 Даны действительные числа x1, y1, x2, y2, ..., x15, y15, которые рассматриваются как координаты (x1, y1), (x2, y2), ..., (x15, y15) точек на плоскости. Выяснить, верно ли, что для каждой из этих пятнадцати точек найдется другая, такая, что все оставшиеся тринадцать точек лежат по одну сторону от прямой, проходящей через эти две точки.
614 Даны целые числа x1, y1, x2, y2, ..., xn, yn. Выяснить, найдутся ли среди точек с координатами (x1, y1), (x2, y2), ..., (xn, yn) четыре таких, которые являются вершинами квадрата.
615 Даны целые числа x1, y1, x2, y2, x3, y13. Известно, что точки с координатами (x1, y1), (x2, y2), (x3, y3) являются тремя вершинами некоторого прямоугольника. Найти координаты четвертой вершины.
616 Прямая на плоскоти может быть задана уравнением ax + by + c = 0, где a и b одновременно не равны нулю. Будем рассматривать прямые только с целыми коэффициентами a, b, c. Пусть даны коэффициенты нескольких прямых : a1, b1, c1, a2, b2, c2, ..., an, bn, cn.
617 Окружность на плоскости может быть задана координатами x, y ее центра и радиусом r. Пусть даны соответствующие характеристики нескольких окружностей: x1, y1, r1, x2, y2, r2, ..., xn, yn, rn.
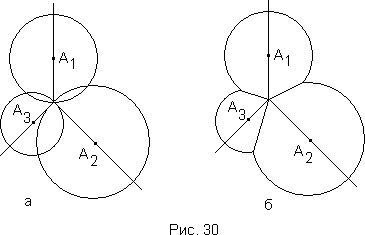
618 Рассматриваются три луча, проведенные в плоскости из точки O. Углы между соседними лучами равны 2π/3. На лучах выбраны точки А1, А2, А3, и из этих точек как из центров проведены окружности, проходящиие через точку О. Считая данными расстояния A1O, A2O, A3O, вычислить площадь фигуры, изображенной на рис.30, a. Для вычисления разбить фигуру на части так, как показано на рис.30, б.
620 Медианой множества, состоящего из четного числа точек плоскости, ни какие три из которых не лежат на одной прямой, называется прямая, соединяющая две точки множества, с обеих сторон от которой лежит равное число точек. Даны действительные числа x1, y1, x2, y2, ..., xn, yn (n - нечетное число). Найти число медиан множества точек с координатами (x1, y1), (x2, y2), ..., (xn, yn) в предположении, что никакие три точки этого множества не лежат на одной поямой.
621 Даны действительные числа а, b, c, d. Выяснить, можно ди прямоугольник со сторонами a, b целиком уместить в прямоугольнике со сторонами c, d ( в отличие от задачи 55, здесь не обязательна взаимная параллельность сторон).
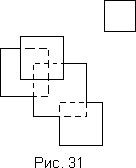
622 Даны действительные числа a1, b1, c1, a2, b2, c2, ..., an, bn, cn. Эта последовательность определяет на плоскости n квадратов со сторонами, параллельными осям: ai, bi - координаты центра квадрата, ci - длина его стороны ( i = 1, ..., n). Определить площадь фигуры, образованной всеми квадратами (рис. 31).
624 Даны действительные числа x1, y1, x2, y2, ..., xn, yn. Известно, что точки p1, p2, ..., pn с координатами (x1, y1), (x2, y2), ..., xn, yn попарно различны. Рассмотрим замкнутую ломаную p1, p2... pn.
625 Даны действительные числа x1, y1, x2, y2, ..., xn, yn. Известно, что точки p1, p2, ..., pn с координатами( x1, y1), (x2, y2), ..., xn, yn попарно различны. Найти выпуклый многоугольник с вершинами в некоторых из точек p1, p2, ..., pn, который содержит все точки p1, p2, ..., pn. Многоугольник должен быть представлен последовательностью вершин.
626 Сетью называется совокупность точек (узлов), некоторые из которых соединены между собой стрелками. Сети, cостоящей из n узлов, можно сопоставить две квадратные матрицы порядка n: матрицу соединений и матрицу связей. Элемент матрицы соединений aij равен 1, если сеть содержит стрелку, ведущую из узла i в узел j, и 0 в противном случае (i, j = 1, ..., n ). Элемент bij матрицы связей равен 1, если из узла i можно попасть в узел j, двигаясь по стрелкам, и 0 в противном случае. Так, для сети, изображенной на рис. 32, матрицы соединений и связей имеют вид
627 Линия называется уникурсальной, если ее можно начертить, не отрывая карандаша от бумаги и не проходя два раза одно и то же звено. Доказать, что линия уникурсальна тогда и только тогда, когда число тех ее узлов, из которых выходит нечетное число звеньев, не превосходит двух. Линии, содержащей n узлов, можно сопоставить квадратную матрицу порядка n - матрицу соединений, элемент aij которой равен 1, если узел i соединен с узлом j некоторым звеном, не содержащим других вершин, и 0 в противном случае ( i, j = 1, ..., n ). Для линии, изображенной на рис.33, матрица соединений имеет вид
607 Дано действительное число φ (0 < φ < π). Из точки ( 1, 1 ) под углом φ к прямой x = 1 выпущен световой луч ( рис. 29, а - 29, б).
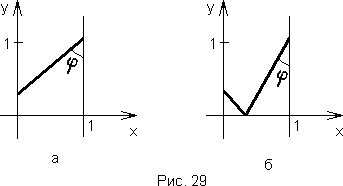
- Найти точку оси ординат, в которой луч
падает на эту ось. Если φ < π / 4, то луч сначала отразится по закону "угол паденя равен углу
отражения" от оси абсцисс.
608 Даны действительные числа x1, y1, x2, y2 (x1≠x2 ), которые определяют две точки A(x1, y1) и B ( x2, y2 ). На оси абсцисс найти точку, сумма расстояний от которой до точек A и B - наименьшая для всех точек этой оси.
609 Даны действительные числа x, y. Вычислить расстояние от точки плоскости с координатами (x, y) до границы квадрата (т. е. минимум расстояний от данной точки до точек границы квадратов) с вершинами:
-
а) ( -0.5, -0.5 ), ( -0.5, 0.5 ), ( 0.5, 0.5 ), ( 0.5, -0.5 );
б) ( 0, 0 ), ( 0, 1 ), ( 1, 1 ), ( 1, 0 ).
610 Даны натуральное число n, целые числа x1, y1, x2, y2, ..., xn, yn. Известно, что точки p1, ..., pn с координатами (x1, y1), (x2, y2), ..., (xn, yn) попарно различны. Пусть точка pi удалена от начала координат на расстояние ri ( i = 1, ..., n ). Пусть R = max ( r1, ..., rn ).
-
а) Среди точек p1, ..., pn выбрать какую - нибудь одну pi, для
которой ri = R; указать координаты выбранной точки и расстояние от этой точки до
начала координат.
б) Среди точек pi (1 ≤ i ≤ n), для которых ri = R, выбрать те, которые обладают наименьшей абсциссой. Если таких точек больше одной, то выбрать из них точку, которая имеет наибольшую ординату. Указать номер выбранной точки.
611 Даны действительные числа a1, ..., a50. Эти числа определяют 25 интервалов числовой оси: ( a1, a2), (a3, a4), ..., (a49, a50).
-
a) Имеют ли все данные интервалы общие точки? Если да, то указать какую-нибудь из этих точек.
б) Является ли интервалом объединение данных интервалов? Если да, то указать концы этого интервала.
в) Указать число i (1 ≤ i ≤ 25) такое, что объединение данных интервалов можно представить в виде i непересекающихся интервалов.
г) Имеются ли точки числовой оси, принадлежащие по крайней мере трем каким - нибудь из данных интервалов? Если да, то указать какую - нибудь из этих точек.
612 Даны действительные числа x1, ..., x15, y1, ..., y15, r1, ..., r15. Выяснить, есть ли на плоскости точка, принадлежащая всем кругам c1, ..., c15, где ci имеет центр с координатами xi, yi и радиус ri( i = 1, ..., 15 ).
613 Даны действительные числа x1, y1, x2, y2, ..., x15, y15, которые рассматриваются как координаты (x1, y1), (x2, y2), ..., (x15, y15) точек на плоскости. Выяснить, верно ли, что для каждой из этих пятнадцати точек найдется другая, такая, что все оставшиеся тринадцать точек лежат по одну сторону от прямой, проходящей через эти две точки.
614 Даны целые числа x1, y1, x2, y2, ..., xn, yn. Выяснить, найдутся ли среди точек с координатами (x1, y1), (x2, y2), ..., (xn, yn) четыре таких, которые являются вершинами квадрата.
615 Даны целые числа x1, y1, x2, y2, x3, y13. Известно, что точки с координатами (x1, y1), (x2, y2), (x3, y3) являются тремя вершинами некоторого прямоугольника. Найти координаты четвертой вершины.
616 Прямая на плоскоти может быть задана уравнением ax + by + c = 0, где a и b одновременно не равны нулю. Будем рассматривать прямые только с целыми коэффициентами a, b, c. Пусть даны коэффициенты нескольких прямых : a1, b1, c1, a2, b2, c2, ..., an, bn, cn.
-
а) Определить, имеются ли среди этих прямых совпадающие или параллельные.
б) Определить, имеются ли три прямые, пересекающиеся в одной точке.
в) Определить, находятся ли данные прямые в общем положении. (Прямые находятся в общем положении, если все они различны, никакие две из них не параллельны и никакие три не пересекаются в одной точке).
617 Окружность на плоскости может быть задана координатами x, y ее центра и радиусом r. Пусть даны соответствующие характеристики нескольких окружностей: x1, y1, r1, x2, y2, r2, ..., xn, yn, rn.
-
а) Определить, имеются ли среди этих окружностей три попарно пересекающихся.
б) Найти среди этих окружностей все уединенные окружности, т.е. такие, которые не имеют общих точек ни с одной из остальных окружностей, не лежат целиком внутри и не заключают внутри себя какой - либо из остальных окружностей.
618 Рассматриваются три луча, проведенные в плоскости из точки O. Углы между соседними лучами равны 2π/3. На лучах выбраны точки А1, А2, А3, и из этих точек как из центров проведены окружности, проходящиие через точку О. Считая данными расстояния A1O, A2O, A3O, вычислить площадь фигуры, изображенной на рис.30, a. Для вычисления разбить фигуру на части так, как показано на рис.30, б.
620 Медианой множества, состоящего из четного числа точек плоскости, ни какие три из которых не лежат на одной прямой, называется прямая, соединяющая две точки множества, с обеих сторон от которой лежит равное число точек. Даны действительные числа x1, y1, x2, y2, ..., xn, yn (n - нечетное число). Найти число медиан множества точек с координатами (x1, y1), (x2, y2), ..., (xn, yn) в предположении, что никакие три точки этого множества не лежат на одной поямой.
621 Даны действительные числа а, b, c, d. Выяснить, можно ди прямоугольник со сторонами a, b целиком уместить в прямоугольнике со сторонами c, d ( в отличие от задачи 55, здесь не обязательна взаимная параллельность сторон).
622 Даны действительные числа a1, b1, c1, a2, b2, c2, ..., an, bn, cn. Эта последовательность определяет на плоскости n квадратов со сторонами, параллельными осям: ai, bi - координаты центра квадрата, ci - длина его стороны ( i = 1, ..., n). Определить площадь фигуры, образованной всеми квадратами (рис. 31).
- Здесь может
оказаться полезным предварительное решение следующей задачи. Стороны двух прямоугольников параллельны
координатным осям. Каждый из прямоугольников задан четырьмя действительными числами - двумя абсциссами и
двумя ординатами. Представить ту часть первого прямоугольника, которая не покрывается вторым прямоугольником,
в виде объединения нескольких прямоугольников, не накладывающихся друг на друга.
624 Даны действительные числа x1, y1, x2, y2, ..., xn, yn. Известно, что точки p1, p2, ..., pn с координатами (x1, y1), (x2, y2), ..., xn, yn попарно различны. Рассмотрим замкнутую ломаную p1, p2... pn.
-
а) Верно ли, что ломаная не имеет самопересечений?
б) В предположении, что ломаная не имеет самопересечений, выяснить, является ли n - угольник p1, p2...pn выпуклым.
625 Даны действительные числа x1, y1, x2, y2, ..., xn, yn. Известно, что точки p1, p2, ..., pn с координатами( x1, y1), (x2, y2), ..., xn, yn попарно различны. Найти выпуклый многоугольник с вершинами в некоторых из точек p1, p2, ..., pn, который содержит все точки p1, p2, ..., pn. Многоугольник должен быть представлен последовательностью вершин.
626 Сетью называется совокупность точек (узлов), некоторые из которых соединены между собой стрелками. Сети, cостоящей из n узлов, можно сопоставить две квадратные матрицы порядка n: матрицу соединений и матрицу связей. Элемент матрицы соединений aij равен 1, если сеть содержит стрелку, ведущую из узла i в узел j, и 0 в противном случае (i, j = 1, ..., n ). Элемент bij матрицы связей равен 1, если из узла i можно попасть в узел j, двигаясь по стрелкам, и 0 в противном случае. Так, для сети, изображенной на рис. 32, матрицы соединений и связей имеют вид

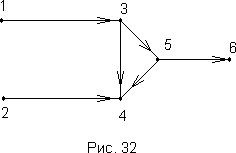
- Дана
матрица соединений некоторой сети из n узлов; получить матрицу связей этой сети.
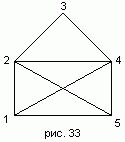
627 Линия называется уникурсальной, если ее можно начертить, не отрывая карандаша от бумаги и не проходя два раза одно и то же звено. Доказать, что линия уникурсальна тогда и только тогда, когда число тех ее узлов, из которых выходит нечетное число звеньев, не превосходит двух. Линии, содержащей n узлов, можно сопоставить квадратную матрицу порядка n - матрицу соединений, элемент aij которой равен 1, если узел i соединен с узлом j некоторым звеном, не содержащим других вершин, и 0 в противном случае ( i, j = 1, ..., n ). Для линии, изображенной на рис.33, матрица соединений имеет вид
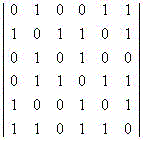
- Дана матрица соединений для
линии с n узлами. Выяснить, является ли линия уникурсальной, и если является, то получить последовательность
номеров узлов, которые будут пройдены во время требуемого вычерчивания.
 Предыдущая глава
Предыдущая глава