658 Дан многочлен Р(х) степени n. Получить многочлен Р2(х).
659 Дан многочлен Р(х) степени n. Получить многочлен Р(Х+1) - Р(х). (Какова степень этого многочлена?).
660 Дан многочлен Р(х) степени n. Получить его производную Р'(х), а так же вычислить Р'(1), Р'(2), Р'(3).
661 Даны действительное число а, многочлен Р(х) степени n. Получить:
662 Даны действительные числа s и t, натуральное число n, действительные числа aо,..., аn. Среди а1,..., аn есть как отрицательные, так и неотрицательные числа. Получить значение Р(s) + Q(t), где в качестве коэффициентов многочлена Р взяты отрицательные члены последовательности aо,..., аn (с хранением порядка их следования), а в качестве коэффициентов многочлена Q - неотрицательные члены (также с хранением порядка их следования)
663 Даны действительные числа s, t, многочлен Р(х) степени n. Найти значение
665 Даны действительные числа ао, а1,..., а5. Получить многочлен шестой степени (х - ао)(х - а1)(х - а5).
666 Даны действительные числа ао,..., а5, dо,..., d5. Получить многочлен шестой степени
do + d1(x - ao) (x - a1) + ... + d5(x - ao)(x - a1) ... (x - a5).
667 Даны действительные числа ао, ... , а5, многочлен Р(х) шестой степени. Получить действительные числа do, ..., dn такие, что
Р(х) = do + d1(x - ao) + d2(x - ao)(x - a1) + d7(x - ao)(x - a1) ... (x - a5).
668 Послеловательность многочленов Тo(x), Т1(x), ... определяется следующим образом: Тo(x) = 1, Т1(x) = х, Тk(x) = 2хТk - 1(x) - Tk - 2(x) (k = 2, 3, ...). Получить Т2(x), ..., Т8(x).
669 Послеловательность многочленов Ho(x), H1(x), ... определяется следующим образом:
670 Последовательность многочленов Go(x), G1(x), ..., определяется следующим образом:
671 Последовательность многочленов Lo(x), L1(x), ... определяется следующим образом:
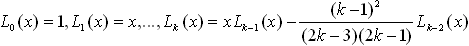 (k = 2, 3, ...).
(k = 2, 3, ...).
672 Даны действительные числа ao, ..., an, bo,...., bn (ao,....., an попарно различны). Требуется найти многочлен F(x) степени не выше, чем n, такой, что F(ai) = bi (i = 0, 1, ..., n).
* Каждый раз, когда в задачах этого раздела говорится, что дан многочлен Р(х) степени n, то подразумевается, что даны действительные числа (коэффииенты) ро,р1, ..., рn такие, что
659 Дан многочлен Р(х) степени n. Получить многочлен Р(Х+1) - Р(х). (Какова степень этого многочлена?).
660 Дан многочлен Р(х) степени n. Получить его производную Р'(х), а так же вычислить Р'(1), Р'(2), Р'(3).
661 Даны действительное число а, многочлен Р(х) степени n. Получить:
-
а) многочлен (х - а) Р(х);
б) многочлен (х2 + 2ах + 3) Р(х);
в) многочлен (х2 + а2) Р(х);
662 Даны действительные числа s и t, натуральное число n, действительные числа aо,..., аn. Среди а1,..., аn есть как отрицательные, так и неотрицательные числа. Получить значение Р(s) + Q(t), где в качестве коэффициентов многочлена Р взяты отрицательные члены последовательности aо,..., аn (с хранением порядка их следования), а в качестве коэффициентов многочлена Q - неотрицательные члены (также с хранением порядка их следования)
663 Даны действительные числа s, t, многочлен Р(х) степени n. Найти значение
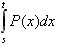
665 Даны действительные числа ао, а1,..., а5. Получить многочлен шестой степени (х - ао)(х - а1)(х - а5).
666 Даны действительные числа ао,..., а5, dо,..., d5. Получить многочлен шестой степени
do + d1(x - ao) (x - a1) + ... + d5(x - ao)(x - a1) ... (x - a5).
667 Даны действительные числа ао, ... , а5, многочлен Р(х) шестой степени. Получить действительные числа do, ..., dn такие, что
Р(х) = do + d1(x - ao) + d2(x - ao)(x - a1) + d7(x - ao)(x - a1) ... (x - a5).
668 Послеловательность многочленов Тo(x), Т1(x), ... определяется следующим образом: Тo(x) = 1, Т1(x) = х, Тk(x) = 2хТk - 1(x) - Tk - 2(x) (k = 2, 3, ...). Получить Т2(x), ..., Т8(x).
669 Послеловательность многочленов Ho(x), H1(x), ... определяется следующим образом:
- Ho(x) = 1, H1(x) =
х, Hk(x) = хHk - 1(x) - (k - 1) - Hk - 2(x) (k = 2, 3, ...).
-
а) Получить Н3(х), Н5(х), Н6(х).
б) Даны действительные числа ао, ..., а6. Получить многочлен аоНо(х) + ... + а6Н6(х).
в) Дано действительное число а. Вычислить Но(а) + ... + Н6(а).
670 Последовательность многочленов Go(x), G1(x), ..., определяется следующим образом:
- Go(x) = 1, G1(x) =
х - 1, Gk(x) = (х - 2k +1) Gk - 1(x) - (k -1)2Gk - 2(x)
(k = 2, 3, ...).
- Выполнить для Go(x), G1(x), ...
задания а), б), в), сформулированные в предыдущей задаче для многочленов Но(х),
Н1(х)....
671 Последовательность многочленов Lo(x), L1(x), ... определяется следующим образом:
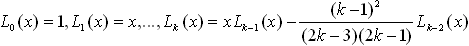 (k = 2, 3, ...).
(k = 2, 3, ...).
-
а) Получить L5(x) и L7(x).
б) Даны действительные числа dо, ..., d8, a. Вычислить do + d1L1a + ... + d8L8(a).
в) Вычислить многочлен Lo(x) + L1(x) + ... + L6(x).
672 Даны действительные числа ao, ..., an, bo,...., bn (ao,....., an попарно различны). Требуется найти многочлен F(x) степени не выше, чем n, такой, что F(ai) = bi (i = 0, 1, ..., n).
- Отметим, что нетрудно
построить многочлены wo(x), w1(x), ..., wn(x),
каждый из которых имеет степень n и которые обладают тем свойством, что wi(x) равен 1 при х =
аi и равен 0 при х = ао, а1, ..., аi - 1, аi + 1, ...,
an - для этого достаточно положить
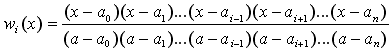 i = 0, 1, ..., n.
i = 0, 1, ..., n.- В качестве искомого многочлега F(x) берётся сумма bowo(x)
+ b1w1(x) + ... + bnwn(x).
* Каждый раз, когда в задачах этого раздела говорится, что дан многочлен Р(х) степени n, то подразумевается, что даны действительные числа (коэффииенты) ро,р1, ..., рn такие, что
- Р(х) = рnxn + рn-1xn-1 +
ho.
- Аналогично, получить многочлен - это значит получить
последовательность его коэффициентов.
 Предыдущая глава
Предыдущая глава