§20 Преобразование и построение матриц

673 Даны действительная матрица размера n x (n + 1) действительные числа a₁, ..., a_n+1, b₁, ..., b_n+1 натуральные числа p, q (p ≤ n, q ≤ n+1). Образовать матрицу размера (n + 1) x (n + 2) вставкой после строки с номером р данной матрицы новой строки с элементами a₁, ..., a_n+1 и последующей вставкой после столбца с номером q нового столбца с элементами b₁, ..., b_n+1.

674 Даны целые числа a₁, ..., a₁₀, целочисленная квадратная матрица порядка n. Заменить нулями в матрице те элементы с чётной суммой индексов, для которых имеются равные среди a₁, ..., a₁₀.

675 Даны действительные числа a₁,...,a_n действительная квадратная матрица порядка n (n ≥ 6). Получить действительную матрицу размера n x (n+1), вставив в исходную матрицу между пятым и шестым столбцами новый столбец с элементами a₁,...,a_n .

676 Дана целочисленная матрица размера 6х9. Найти матрицу получающуюся из данной:
a) перестановкой столбцов - первого с последним, второго с предпоследним и т.д.
б) перестановкой строк - первой с последней, второй с пердпоследней и т.д.

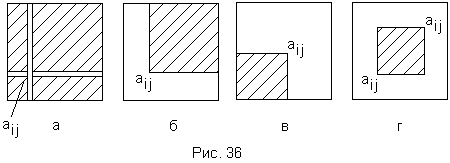
677 Дана действительная матрица [a_ij]_{i, i = 1, ..., n}. Получить действительную матрицу [b_ij]_{i, i = 1, ..., n} элемент b_ij

которой равен сумме элементов данной матрицы расположенных в области, определяемой индексами i,j так, как показано на рисунке 36 (а - г) (область заштрихована). Сходным образом можно рассмотреть вместо суммы элементов их произведение, наибольшее значение, наименьшее значение.

678 Дана действительная квадратная матрица, порядка n. Преобразовать матрицу по правилу: строку с номером n сделать столбцом с номером n, а столбец с номером n сделать строкой с номером n.

679 Даны две действительные квадратные матрицы порядка n. Получить новую матрицу:
а) умножением элементов каждой строки первой матрицы на наибольшее из значений элементов соответствующей строки второй матрицы;
б) прибавлением к элементам каждого столбца первой матрицы произведения элементов соответствующих строк второй матрицы.

680 В данной действительности матрице размера n x m (n ≥ 3, m ≥ 3) поменять местами:
а) строки с номерами 2 и n-1
б) столбцы с номерами 3 и n-2

681 Даны действительные числа b₁, ..., b₁₅. В действительной матрице [a_ij]_{i , i = 1 ,..., 17; j = 1, ..., 10} первая и последняя строки заполнены нулями: a_{1 1} = a_{1 2} = ... = a_{1 10} = a_{17 1} = a_{17 2} = ... = a_{17 10} = 0. Элементы a_{2 1}, a_{3 1}, a_{16 1} первого столбца соответственно равны b₁, ..., b₁₅. Известно, что при 2 ≤ i ≤ 16, 2 ≤ j ≤ 10 имеет место a_ij = (1/2)(a_{i+1 j-1} + a_{i-1 j-1}). Требуется определить a_{2 10}, a_{3 10}, ..., a_{16 10}.

682 Даны целочисленная матрица размера n x 3, целые числа k, l (1 ≤ k ≤ n, 1 ≤ l ≤ n, k ≠ l). Преобразовать матрицу так, чтобы строка с исходным номером k непосредственно следовала за строкой с исходным номером l, сохранив порядок следования остальных строк.

683 Назовем допустимым преобразованием матрицы перестановку двух строк или двух столбцов. Дана действительная квадратная матрица порядка n. С помощью допустимых преобразований добиться того, чтобы
а) один из элементов матрицы, обладающий наибольшим по модулю значением, располагался в левом верхнем углу матрицы;
б) один из элементов матрицы, обладающий наименьшим значением, располагался в левом нижнем углу матрицы.

684 В данной действительной квадратной матрице порядка n найти наибольший по модулю элемент. Получить квадратную матрицу порядка n-1 путем выбрасывания из исходной матрицы какой-нибудь строки и столбца, на пересечении которых расположен элемент G найденным значением.

685 Дана действительная квадратная матрица порядка n, все элементы которой различны. Найти наибольший элемент среди стоящих на главной и побочной диагоналях и поменять его местами с элементом, стоящим на пересечении этих диагоналей.

686 Пгостроить квадратную матрицу порядка 2n:

687 Дано действительное число х. Получить квадратную матрицу порядка 10:

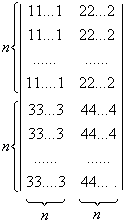
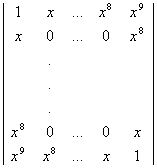
(Середина заполняется нулями).
688 Даны действительные числа a₁,...,a_n. Поучить квадратную матрицу порядка n:

689 Получить целочисленную квадратную матрицу порядка 7, элементами которой являются числа 1, 2, ..., 49, расположенные в ней по спирали (рис. 37).


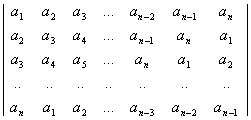
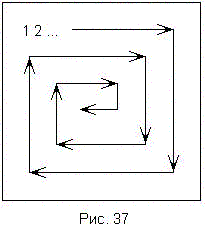
690 Дана действительная квадратная матрица порядка 7. Найти последовательность действительных чисел b₁,...,b₄₉ получающуюся при чтении данной матрицы по спирали (см. предыдущую задачу).

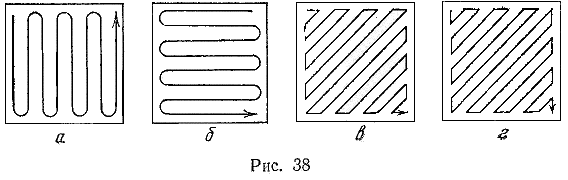
691 Даны действительные числа a₁,...,a₆₄. Получить действительную квадратную матрицу порядка 8, элементами которой являются числа a₁,..., a₆₄, расположенные в ней по схеме, которая приведена на рис. 38, а-г.



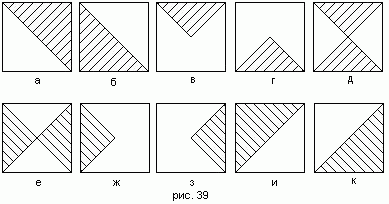
692 Дана действительная квадратная матрица порядка n. Найти наибольшее из значений элементов, расположенных в заштрихованной части матрицы (рис. 39).




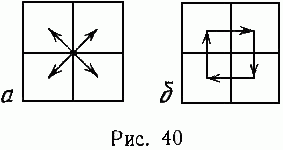
693 Дана действительная квадратная матрица порядка 2n. Получить новую матрицу, переставляя ее блоки размера n x n
а) в соответствии с рис. 40, а;
б) в соответствии с рис. 40, б


694 Получить квадратную матрицу порядка n:


695 Таблица футбольного чемпионата, в котором участвовало n команд (см. задачу 413), задана своей верхней правой частью в виде последовательности чисел 0, 1 или 2: первые n-1 чисел последовательности относятся к первой строке таблицы, следующие n-2 чисел-ко второй и т. д. Построить таблицу целиком, т. е. получить соответствующую квадратную матрицу порядка n (элементы главной диагонали заполняются нулями).

696 Имеется тблица футбольного чемпионата, в котором участвовало n команд (см. задачу 413). Таблица представлена целочисленной квадратной матрицей порядка n, элементы главной диагонали этой матрицы равны нулю. Перестроить эту таблицу, присвоив каждой команде номер, равный занятому ею месту (для простоты считается, что при равном числе очков места распределяются произвольно). Отдельно указать распределение команд в старой нумерации по занятым ими местам.

Предыдущая глава

К началу

Следующая глава