720 Даны действительные числа x1,..., xn, y1,...,
yn, t1,..., tm (x1 < x2 <...< xn, x
1 ≤ ti ≤ xn, i = 1,...,m). Число y представляет собой значение некоторой
функции f от аргумента; yj = f (xj) (j = 1,...,n).С помощью линейной интерполяции получить
значения f (t1), f (t2),...,f (tm).
721 Даны действительные числа h, x1,..., xn, y1,..., yn.Всё сказанное о x1,..., xn, y1,..., yn в предыдущей задаче остаётся в силе. С помощью линейной интерполяции получить значения функции f для значений аргументов, равных x1, x1+h, x1+2h,...,x1+kh, где k - наибольшее целое, для которого x1+kh ≤ xn.
722 Даны натуральное число n, действительные числа x1,..., xn, y1,..., yn. Рассмотреть предыдущую задачу, считая что h=(xn - x1)/n (ответом должна служить последовательность, содержащая n+1 число).
723 Даны действительные числа x1,..., xn, y1,..., yn, t (x1 < x2 <...<xn, y1 ≤ t ≤ yn). Предполагается, что y1,..., yn представляют собой результаты измерения температуры воздуха в моменты времени x1,..., xn. С помощью линейной интерполяции указать все моменты времени, в которые температура воздуха была равна t (не исключён случай yj = yj + 1 = t для некоторых j (1 ≤ j ≤ n-1)).
724 Вернуться к задачам 721, 723, считая, что разности между соседними известными значениями аргумента x1,..., xn равны между собой: xn-xn-1 = xn-1 - xn-2 = .. .= x2 - x1 = h. Вместо x1,..., xn задаются x1 и h, порядок остальных исходных данных не изменяется.
725 Дано действительное положительное число ε. Методом деления отрезка пополам найти приближённое значение корня уравнения f (x) = 0. Абсолютная погрешность найденного значения не должна превосходить ε. (Ниже, рядом с уравнением f (x) = 0, дополнительно указан отрезок, содержащий корень.)
726 Дано действительное положительное число ε. Методом хорд вычислить с точностью ε *) корень уравнения f (x) = 0 (ниже, следом за уравнением f (x) = 0, дополнительно задан отрезок, содержащий корень):
727 Вернуться к предыдущей задаче, считая, что построение приближений к корню уравнения f (x) = 0 следует закончить, когда будет получено такое приближение x, для которого | f ( x ) | < ε. (Этот подход к оценке точности может быть приемлемым только в тех случаях, когда известно, что |f (x)| не принимает значений меньше ε при значениях x, удалённых от корня уравнения f (x) = 0; рис.41, а, б)
729Дано действительное положительное число ε. Методом касательных вычислить с точностью ε корень уравнения f (x) = 0 (ниже, следом за уравнением f (x) = 0, в скобках указано начальное приближение к корню):
730 Решить методом касательных перечисленные в предыдущей задаче уравнения, прекращая построения приближений к корню уравнения f (x) = 0 в тот момент, когда будет получено такое приближение x, для которого |f (x)| < 0.00001.
731Дано действительное положительное число ε. Методом интерации вычислить с точностью ε корень уравнения f (x) = 0 (ниже, следом за уравнением f (x) = 0, в скобках указано начальное приближение к корню):
732 Сравнить методы деления отрезка попалам, хорд, касательных и интерации, поочерёдно используя их для решения одного и того же уравнения. Независимо от метода построения приближений к корню уравнения f (x) = 0 следует заканчивать, как только будет получено такое приближение x, для которого |f (x)|< ε. Значенеие ε следует поочерёдно брать равным 0.01, 0.001, ..., 0.0000001. Для каждого из методов построить график или столбчатую диаграмму изменения числа потребовавшихся приближений при переходе от одного значения ε к другому. В качестве уравнения, на котором проводится сравнение методов, и отрезка, которому принадлежит корень, следует взять:
733 Дано действительное положительное число ε. Найти с помощью подходящих методов все корни уравнения f (x) = 0 с точностью ε. Для получения отрезков, содержащих по одному корню уравнения f (x), или для получения начальнх приближений к корням исследовать график функции y = f (x). В качестве f (x) рассмотреть:
734 Найти с точностью 0.00001 наименьший корень уравнения:
735 Вернуться к предыдущей задаче, рассматривая вместо наименьшего корня:
736 Найти с точностью 0.0001 все корни уравнения 1/x = sin x, принадлежащего отрезку [-π, π].
737 Для каждого целого числа n из диапозона от 1 до 50 найти подходящим методом с точностью 1/n2 наибольший корень уравнения (x3/n2) - 3x2 + 1 = 0 (этот корень, как нетрудно показать, меньше, чем 3n2). Получить графическое изображение зависимости значения наибольшего корня от n.
738 Иногда функция y = f (x) задаётся на некотором отрезке с помощью уравнений вида F(x,y) = 0. Вычислить значения функции, заданой уравнением:
739 Написать программу решения по методу Гаусса системы уравнений
740 Дано действительное положительное число ε. Методом итерации решить систему линейных алгебраических уравнений с точностью ε. В данной задаче вычисление с точностью ε означает следуещее. Вычисляется последовательность векторов - приближений x(m) = (x1 (m),x2 (m) ..., xn (m)), где n - число неизвестных системы, m = 0,1,2, ... Если для некоторого k выполнено условие
741 Вычислить интегралы по формулам численного интегрирования и по формуле Ньютона-Лейбница. Сравнить результаты:
а)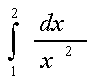 ;
б)
;
б) 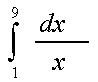 ;
в)
;
в) 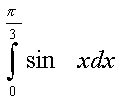 ;
;
г)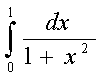 ;
д)
;
д) 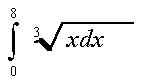 .
.
742 Дано действительное число ε. Вычислить интегралы с точностью ε. В данной задаче вычисление с точностью ε означает следующее. Отрезок интегрирования разбивается на ni равных частей и строится сумма Sni, котороя является приближенным значением интеграла. Если выполняется условие |Sni+1 - Sni| < ε, Sni+1 считается значением интеграла с точностью ε. (Здесь ni < ni+1 (i = 1, 2, ...).)
а)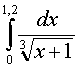 ;
б)
;
б) 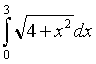 ;
в)
;
в) 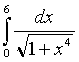 ;
г)
;
г) 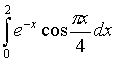 ;
;
д)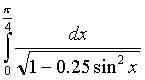 ;
е)
;
е) 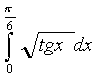 ;
ж)
;
ж) 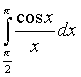 ;
з)
;
з) 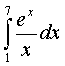 ;
;
и)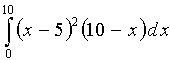 ;
к)
;
к) 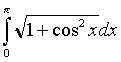 ;
л)
;
л) 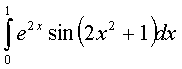 ;
;
м)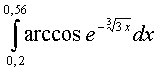 ;
н)
;
н) 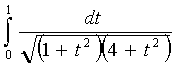 ;
о)
;
о) 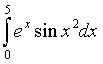 ;
;
п)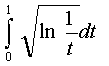 .
.
Если удается с помощью формулы Ньютона-Лейбница найти точное значение интеграла, то полезно сранить с ним результат приближенного вычисления.
743 Вычислить длину эллипса по формуле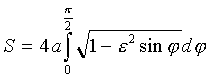 ,
a = 30, b = 20 (a и b-полуоси эллипса),
,
a = 30, b = 20 (a и b-полуоси эллипса), 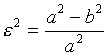 .
.
744 Вернуться к задаче 738. Найти приближенные значения интегралов функций y = f (x), определенных в а) и б) с помощью уравнений вида F(x, y) = 0. Первая функция интегрируется на отрезке [-1,0], вторая - на отрезке [1,2]. Вычисление интеграла следует начинать, разделив отрезок интегрирования на 5 частей. Затем уточнить значение интеграла, уменьшая шаг вдвое. Вычисление проводить с точностью 0.001. Значение функции вычислять с точностью 0.00001.
745 Дано действительное положительное число ε. Вычислить с точностью ε площадь фигуры между дугами кривых:
а) y = sin x2 + 2, y = e x2;
б) y = 2x2, y = cos x 2 + 1;
Воспользоваться численными методами решения уравнений и интегрирования.
746 Решить дифференциальное уравнение y' = f (x, y). После уравнения в скобках записаны исходные данные для решения: x0 - начальное значиние аргумента, y0 - начальное значение функции от x0, отрезок, на котором решается уравнение, h - шаг.
а) y՛ = x + cos( y/π ) (x0=1.7, y0 = 5.3, [1.7, 5.2], h = 0.15);
б)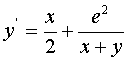 (x0 = 1.8, y0 = 4.5,
[1.8, 4.6], h = 0.1);
(x0 = 1.8, y0 = 4.5,
[1.8, 4.6], h = 0.1);
в)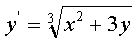 (x0 = 3, y0 = 5, [3, 11.4], h = 0.3);
(x0 = 3, y0 = 5, [3, 11.4], h = 0.3);
г)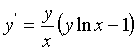 (x0 = 1, y0 = 0.5, [1, 0.6], h = 0.005);
(x0 = 1, y0 = 0.5, [1, 0.6], h = 0.005);
д) y՛ = 2x + sin( y/x ) (x0 = 0, y0 = 1, [0, 1], h = 0.1);
е)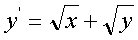 (x0 = 0, y0 = 0, [0, 1], h = 0.1);
(x0 = 0, y0 = 0, [0, 1], h = 0.1);
ж)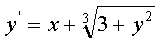 (x0 = 0, y0 = 0, [0, 1], h = 0.1);
(x0 = 0, y0 = 0, [0, 1], h = 0.1);
з)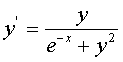 (x0 = 0, y0 = 1, [0, 1], h = 0.01);
(x0 = 0, y0 = 1, [0, 1], h = 0.01);
и) y ՙ = x - y (x0 = 0, y0 = 0 , [0, 1], h = 0.05);
к)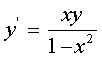 (x0 = 0, y0 = 1, [0, 0.5], h = 0.05);
(x0 = 0, y0 = 1, [0, 0.5], h = 0.05);
л) y' = 2xy (x0 = 0, y0 = 1, [0, 1], h = 0.025);
м) y ՙ = 2x - 3y (x0 = 0, y0 = 0, [0, 1], h = 0.1);
н)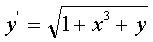 (x0 = 0.8, y0 = 3.8,
[0.8, 5.0], h = 0.15).
(x0 = 0.8, y0 = 3.8,
[0.8, 5.0], h = 0.15).
*) Когда заходит речь о "вычислении с точностью ε", следует иметь ввиду, что лишь немногмие чисенные методы, основанные на построении последовательных приближений x0, x1, ... к искомому числу х, гарантируют, подобно методу деления отрезка пополам, что абсолютная погрешность найденного значения будет меньше ε. Будем считать, что требуемая точность ε достигнута, как только получено такое xm (при m > 1), для которого |xm - xm-1| < ε. В данной задаче предполагается, что в программе будет реализован именно этот подход к оценке точности.
721 Даны действительные числа h, x1,..., xn, y1,..., yn.Всё сказанное о x1,..., xn, y1,..., yn в предыдущей задаче остаётся в силе. С помощью линейной интерполяции получить значения функции f для значений аргументов, равных x1, x1+h, x1+2h,...,x1+kh, где k - наибольшее целое, для которого x1+kh ≤ xn.
722 Даны натуральное число n, действительные числа x1,..., xn, y1,..., yn. Рассмотреть предыдущую задачу, считая что h=(xn - x1)/n (ответом должна служить последовательность, содержащая n+1 число).
723 Даны действительные числа x1,..., xn, y1,..., yn, t (x1 < x2 <...<xn, y1 ≤ t ≤ yn). Предполагается, что y1,..., yn представляют собой результаты измерения температуры воздуха в моменты времени x1,..., xn. С помощью линейной интерполяции указать все моменты времени, в которые температура воздуха была равна t (не исключён случай yj = yj + 1 = t для некоторых j (1 ≤ j ≤ n-1)).
724 Вернуться к задачам 721, 723, считая, что разности между соседними известными значениями аргумента x1,..., xn равны между собой: xn-xn-1 = xn-1 - xn-2 = .. .= x2 - x1 = h. Вместо x1,..., xn задаются x1 и h, порядок остальных исходных данных не изменяется.
725 Дано действительное положительное число ε. Методом деления отрезка пополам найти приближённое значение корня уравнения f (x) = 0. Абсолютная погрешность найденного значения не должна превосходить ε. (Ниже, рядом с уравнением f (x) = 0, дополнительно указан отрезок, содержащий корень.)
-
а) x + ln(x + 0.5) - 0.5 = 0, [0, 2];
б) x5 - x - 0.2 = 0, [1, 1.1];
в) x4 + 2x3 - x - 1 = 0, [0, 1];
г) x3 - 0.2x2 - 0.2x - 1.2 = 0, [1, 1.5];
д) (2sin2x)/3 - (3cos2x)/4 = 0, [0, π/2];
е) x4 + 0.8x3 - 0.4x2 - 1.4x - 1.2 = 0, [-1.2, -0.5];
ж) x4 - 4.1x3 + x2 - 5.1x + 4.1 = 0, [3.7, 5];
726 Дано действительное положительное число ε. Методом хорд вычислить с точностью ε *) корень уравнения f (x) = 0 (ниже, следом за уравнением f (x) = 0, дополнительно задан отрезок, содержащий корень):
-
а) x2x - 1 = 0, [0, 1];
б) x2 - sin5x = 0, [0.5, 0.6];
в) (2sin22x)/3 - (3cos22x)/4 = 0, [0, π/4];
г) x3 - 2x2 + x - 3 = 0, [2.1, 2.2];
д) (4 + x2)(ex - e-x) = 18, [1.2, 1.3];
е) x4 + 0.5x3 - 4x2 - 3x - 0.5 = 0, [-1, 0];
ж) x2 - 1.3ln(x + 0.5) - 2.8x + 1.15 = 0, [2.1, 2.5];
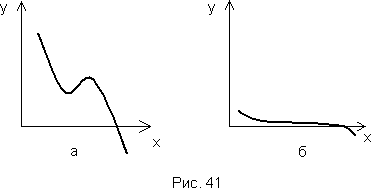
727 Вернуться к предыдущей задаче, считая, что построение приближений к корню уравнения f (x) = 0 следует закончить, когда будет получено такое приближение x, для которого | f ( x ) | < ε. (Этот подход к оценке точности может быть приемлемым только в тех случаях, когда известно, что |f (x)| не принимает значений меньше ε при значениях x, удалённых от корня уравнения f (x) = 0; рис.41, а, б)
729Дано действительное положительное число ε. Методом касательных вычислить с точностью ε корень уравнения f (x) = 0 (ниже, следом за уравнением f (x) = 0, в скобках указано начальное приближение к корню):
-
а) x3 - 2x2 + x - 3 = 0, (2.2);
б) tg x - x = 0, (4.67);
в) 1.8x4 - sin 10x = 0, (0.22);
г) x4 - 3x2 + 75x - 10 000 = 0, (-11);
д) x3 - 6x2 + 20 = 0, (2.31).
730 Решить методом касательных перечисленные в предыдущей задаче уравнения, прекращая построения приближений к корню уравнения f (x) = 0 в тот момент, когда будет получено такое приближение x, для которого |f (x)| < 0.00001.
731Дано действительное положительное число ε. Методом интерации вычислить с точностью ε корень уравнения f (x) = 0 (ниже, следом за уравнением f (x) = 0, в скобках указано начальное приближение к корню):
-
а) x - (sin x )/2 - 1 = 0, (0);
б) 2x3 + 4x - 1 = 0, (0.11);
в) x3 + 12x - 2 = 0, (0.95);
г) 5x - 8 ln x = 8, (4.32);
д) x3 + x = 1000, (9.42);
е) x - sin x = 0.25, (1.17);
ж) x3 - 6x2 + 20 = 0, (2.25);
з) 5x3 + 10x2 + 5x - 1 = 0, (0.6);
732 Сравнить методы деления отрезка попалам, хорд, касательных и интерации, поочерёдно используя их для решения одного и того же уравнения. Независимо от метода построения приближений к корню уравнения f (x) = 0 следует заканчивать, как только будет получено такое приближение x, для которого |f (x)|< ε. Значенеие ε следует поочерёдно брать равным 0.01, 0.001, ..., 0.0000001. Для каждого из методов построить график или столбчатую диаграмму изменения числа потребовавшихся приближений при переходе от одного значения ε к другому. В качестве уравнения, на котором проводится сравнение методов, и отрезка, которому принадлежит корень, следует взять:
-
а) x3 + x2 - 3 = 0, [0.6, 1.4];
б) x5 - x - 0.2 = 0, [0.9, 1.1];
в) 5x3 - x - 1 = 0, [0.6, 0.8];
г) x3 - 2x - 5 = 0, [1.9, 2.93];
д) x3 + x = 1000, [9.1, 10];
е) x4 + 2x3 - x - 1 = 0, [0, 1].
- Для метода касательных и интерации в качестве начального приближения
выбирается подходящий конец отрезка.
733 Дано действительное положительное число ε. Найти с помощью подходящих методов все корни уравнения f (x) = 0 с точностью ε. Для получения отрезков, содержащих по одному корню уравнения f (x), или для получения начальнх приближений к корням исследовать график функции y = f (x). В качестве f (x) рассмотреть:
-
а) x3 - 6x2 + 12x + 5 = 0;
б) x6 + x2 - 2 = 0;
в) x3 + 3x + 2 = 0;
г) √x + 1 = cos(0.5x);
д) 3x2 - cos2x - 1 = 0;
е) 2 ln x - 1/x + 0.5 = 0;
ж) x4 - 6x3 + 9x2 - 16 = 0.
734 Найти с точностью 0.00001 наименьший корень уравнения:
-
а) x3 - 6x2 + 19.8 = 0;
б) x4 + x3 - 10x2 - 34x - 25 = 0;
в) x3 - 1.75x + 0.75 = 0;
г) x5 + 5x4 - 2x3 - 4x2 + 7x - 3 = 0;
д) 3x - sin x = 7;
е) x8 - 0.4x3 - 1.24 = 0;
ж) x = cos x + 1;
з) e-x = 0.5 + √x;
и) x4 + 39x3 + 958x2 - 1081x - 1987 = 0.
- Использовать какой-нибудь подходящий численный метод решения уравнений.
Для получения отрезка, содержащего наименьший корень уравнения f (x) = 0, или для получения начального приближения
к этому корню исследовать график функции y = f (x).
735 Вернуться к предыдущей задаче, рассматривая вместо наименьшего корня:
-
а) наибольший;
б) наименьший отрицательный;
в) наибольший положительный;
г) второй по величине;
д) наименьший по модулю.
736 Найти с точностью 0.0001 все корни уравнения 1/x = sin x, принадлежащего отрезку [-π, π].
737 Для каждого целого числа n из диапозона от 1 до 50 найти подходящим методом с точностью 1/n2 наибольший корень уравнения (x3/n2) - 3x2 + 1 = 0 (этот корень, как нетрудно показать, меньше, чем 3n2). Получить графическое изображение зависимости значения наибольшего корня от n.
738 Иногда функция y = f (x) задаётся на некотором отрезке с помощью уравнений вида F(x,y) = 0. Вычислить значения функции, заданой уравнением:
-
а) y3 + x3 - 2xy = 0 для x = 0, -0.1, -0.2,..., -1;
б) y3 + y2 - x2 = 0 для x = 1, 1.1, 1.2,..., 2.
- В первом случае функция определена и неотрицательна на отрезке [-1, 0],
её значения на этом отрезке меньше, чем 1; во втором случае функция определена и отрицательна на отрезке
[1, 2], её значение на этом отрезке меньше, чем 1.5. Для нахождения значений y использовать подходящий
численный метод решения уравнений. Вычисление проводить с точностью 0.0001.
739 Написать программу решения по методу Гаусса системы уравнений
a11x1+...+a1nxn = b1,
an1x1+...+annxn = bn,
- Квадратная матрица [aij]i,j=1,...,n и вектор
b1,...,bn - исходные данные задачи (предполагается, что система совместна и имеет
единственное решение).
- Применить программу для решения следующих систем:
-
а) 10x1 + x2 + x3 = 12,
2x1 + 10x2 + x3 = 13,
2x1 + 2x2 + 10x3 = 14;
б) 4x1 + 0,24x2 - 0,08x3 = 8,
0,09x1 + 3x2 - 0,15x3 = 9,
0,04x1 - 0,08x2 + 4x3 = 20;
в) 6x1 - x2 - x3 = 11.33,
- x1 + 6x2 - x3 = 32,
- x1 - x2 + 6x3 = 42;
г) 3x1 - x2 = 5,
- 2x1 + x2 - x3 = 0,
2x1 - x2 + 4x3 = 15;
д) 0,427x1 + 3,210x2 - 1,307x3 = 2,425,
4.270x1 - 0.513x2 + 1.102x3 = - 0.176,
0.012x1 + 1.273x2 - 4.175x3 = 1.423;
е) 10x1 - x2 + 2x3 - 3x4 = 0,
x1 - 10x2 - x3 + 2x4 = 0,
2x1 + 3x2 + 20x3 - x4 = - 10,
3x1 + 2x2 + x3 + 20x4 = 15;
ж) 2x1 + 3x2 - 4x3 + x4 - 3.1 = 0,
0.1x1 - 2x2 - 5x3 + x4 - 2 = 0,
0.15x1 - 3x2 + x3 - 4x4 - 1 = 0,
10x1 + 2x2 - x3 + 2.1x4 + 4.7 = 0;
з) 3x1 + 1.5x2 - x3 + 2.4x4 = 6,
- 0.5x1 + x2 - 3.1x3 - 4x4 = - 12,
2x1 - 0.8x2 - x4 = 1,
x1 - 1.3x2 + 3.9x3 - 3.7x4 = 3.1;
и) 4.13x1 - 2.87x2 - 1.94x3 + 0.61x4 = 0.32,
1.27x1 + 7.23x2 - 0.15x3 + 1.71x4 = - 4.16,
0,19x1 + 2.75x2 + 3.14x3 - 0.76x4 = 2.33,
2.87x1 + 4.33x2 - 2.41x3 - 3.42x4 = 2.79;
к) x1 + 3x2 - 2x3 - 2x5 = 0.5,
3x1 + 4x2 - 5x3 + x4 - 3x5 = 5.4,
- 2x1 - 5x2 + 3x3 - 2x4 + 2x5 = 5,
x2 - 2x3 + 5x4 + 3x5 = 7.5,
- 2x1 - 3x2 + 2x3 + 3x4 + 4x5 = 3.3;
л) 7.9x1 + 5.6x2 + 5.7x3 - 7.2x4 = 6.68,
8.5x1 - 4.8x2 + 0.5x3 + 3.5x4 = 9.95,
4.3x1 + 4.2x2 - 3.2x3 + 9.3x4 = 8.6,
3.2x1 - 1.4x2 - 8.9x3 + 8.3x4 = 1;
м) 10.2x1 + 6.07x2 - 9.1x3 + 50.3 = 0,
9.28x1 - 79.6x2 - 4.92x3 + 25.8 = 0,
68.3x1 - 2.71x2 - 8.14x3 + 32.6 = 0.
740 Дано действительное положительное число ε. Методом итерации решить систему линейных алгебраических уравнений с точностью ε. В данной задаче вычисление с точностью ε означает следуещее. Вычисляется последовательность векторов - приближений x(m) = (x1 (m),x2 (m) ..., xn (m)), где n - число неизвестных системы, m = 0,1,2, ... Если для некоторого k выполнено условие
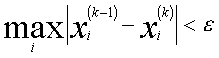 , i = 1,2, ..., n,
, i = 1,2, ..., n,
-
а) x1 = 2 - 0.06x2 + 0.02x3 ,
x2 = 3 - 0.03x1 + 0.05x3 ,
x3 = 5 - 0.01x1 + 0.02x2 ;
б) x1 = 1.2 - 0.1x2 - 0.1x3 ,
x2 = 1.3 - 0.2x1 - 0.1x3 ,
x3 = 1.4 - 0.2x1 - 0.2x2 ;
в) x1 = 0.1x2 - 0.2x3 + 0.3x4,
x2 = - 0.1x1 + 0.1x3 - 0.2x4 + 0.5,
x3 = - 0.1x1 - 0.15x2 + 0.05x4 - 0.5,
x4 = - 0.15x1 - 0.1x2 - 0.005x3 + 0.75;
г) x1 = -0.2x2 + 0.1x3 - 0.2x4 - 0.4,
x2 = 0.2x1 - 0.2x3 + 0.2,
x3 = 0.2x1 - 0.4x2 + 0.2x4 - 0.4,
x4 = 0.333x1 - 1.111;
д) x1 = 0.12x1 - 0.18x2 + 0.08x3 - 0.64,
x2 = 0.15x1 + 0.06x2 - 0.11x3 + 0.26,
x3 = 0.04x1 - 0.1x2 - 0.09x3 + 1.34;
е) x1 - 0.1x2 + 0.2x3 = 0.3,
0.1x1 + x2 - 0.1x3 - 0.1x4 = - 0.2,
-0.1x2 + x3 - 0.1x4 = 0.1,
-0.1x2 + 0.1x3 + x4 = 0.2 ;
ж) 5.92x1 - 1.24x2 - 1.84x3 = 2.44 ,
2.72x1 - 9.71x2 + 2.43x3 = 2.4,
1.76x1 - 3.12x2 + 9.38x3 = 1.93.
741 Вычислить интегралы по формулам численного интегрирования и по формуле Ньютона-Лейбница. Сравнить результаты:
а)
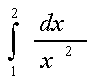 ;
б)
;
б) 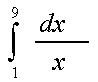 ;
в)
;
в) 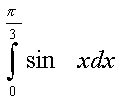 ;
;г)
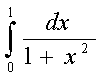 ;
д)
;
д) 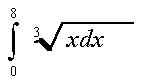 .
.
742 Дано действительное число ε. Вычислить интегралы с точностью ε. В данной задаче вычисление с точностью ε означает следующее. Отрезок интегрирования разбивается на ni равных частей и строится сумма Sni, котороя является приближенным значением интеграла. Если выполняется условие |Sni+1 - Sni| < ε, Sni+1 считается значением интеграла с точностью ε. (Здесь ni < ni+1 (i = 1, 2, ...).)
а)
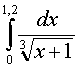 ;
б)
;
б) 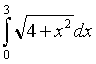 ;
в)
;
в) 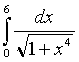 ;
г)
;
г) 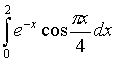 ;
;д)
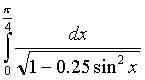 ;
е)
;
е) 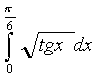 ;
ж)
;
ж) 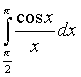 ;
з)
;
з) 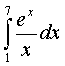 ;
;и)
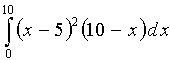 ;
к)
;
к) 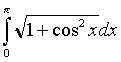 ;
л)
;
л) 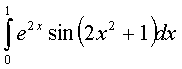 ;
;м)
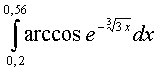 ;
н)
;
н) 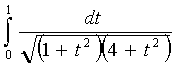 ;
о)
;
о) 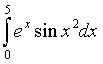 ;
;п)
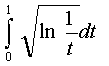 .
.Если удается с помощью формулы Ньютона-Лейбница найти точное значение интеграла, то полезно сранить с ним результат приближенного вычисления.
743 Вычислить длину эллипса по формуле
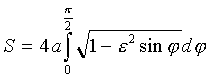 ,
a = 30, b = 20 (a и b-полуоси эллипса),
,
a = 30, b = 20 (a и b-полуоси эллипса), 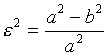 .
.744 Вернуться к задаче 738. Найти приближенные значения интегралов функций y = f (x), определенных в а) и б) с помощью уравнений вида F(x, y) = 0. Первая функция интегрируется на отрезке [-1,0], вторая - на отрезке [1,2]. Вычисление интеграла следует начинать, разделив отрезок интегрирования на 5 частей. Затем уточнить значение интеграла, уменьшая шаг вдвое. Вычисление проводить с точностью 0.001. Значение функции вычислять с точностью 0.00001.
745 Дано действительное положительное число ε. Вычислить с точностью ε площадь фигуры между дугами кривых:
а) y = sin x2 + 2, y = e x2;
б) y = 2x2, y = cos x 2 + 1;
Воспользоваться численными методами решения уравнений и интегрирования.
746 Решить дифференциальное уравнение y' = f (x, y). После уравнения в скобках записаны исходные данные для решения: x0 - начальное значиние аргумента, y0 - начальное значение функции от x0, отрезок, на котором решается уравнение, h - шаг.
а) y՛ = x + cos( y/π ) (x0=1.7, y0 = 5.3, [1.7, 5.2], h = 0.15);
б)
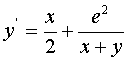 (x0 = 1.8, y0 = 4.5,
[1.8, 4.6], h = 0.1);
(x0 = 1.8, y0 = 4.5,
[1.8, 4.6], h = 0.1);в)
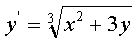 (x0 = 3, y0 = 5, [3, 11.4], h = 0.3);
(x0 = 3, y0 = 5, [3, 11.4], h = 0.3);г)
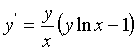 (x0 = 1, y0 = 0.5, [1, 0.6], h = 0.005);
(x0 = 1, y0 = 0.5, [1, 0.6], h = 0.005);д) y՛ = 2x + sin( y/x ) (x0 = 0, y0 = 1, [0, 1], h = 0.1);
е)
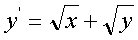 (x0 = 0, y0 = 0, [0, 1], h = 0.1);
(x0 = 0, y0 = 0, [0, 1], h = 0.1);ж)
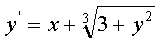 (x0 = 0, y0 = 0, [0, 1], h = 0.1);
(x0 = 0, y0 = 0, [0, 1], h = 0.1);з)
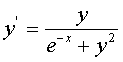 (x0 = 0, y0 = 1, [0, 1], h = 0.01);
(x0 = 0, y0 = 1, [0, 1], h = 0.01);и) y ՙ = x - y (x0 = 0, y0 = 0 , [0, 1], h = 0.05);
к)
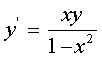 (x0 = 0, y0 = 1, [0, 0.5], h = 0.05);
(x0 = 0, y0 = 1, [0, 0.5], h = 0.05);л) y' = 2xy (x0 = 0, y0 = 1, [0, 1], h = 0.025);
м) y ՙ = 2x - 3y (x0 = 0, y0 = 0, [0, 1], h = 0.1);
н)
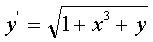 (x0 = 0.8, y0 = 3.8,
[0.8, 5.0], h = 0.15).
(x0 = 0.8, y0 = 3.8,
[0.8, 5.0], h = 0.15).*) Когда заходит речь о "вычислении с точностью ε", следует иметь ввиду, что лишь немногмие чисенные методы, основанные на построении последовательных приближений x0, x1, ... к искомому числу х, гарантируют, подобно методу деления отрезка пополам, что абсолютная погрешность найденного значения будет меньше ε. Будем считать, что требуемая точность ε достигнута, как только получено такое xm (при m > 1), для которого |xm - xm-1| < ε. В данной задаче предполагается, что в программе будет реализован именно этот подход к оценке точности.
 Предыдущая глава Предыдущая глава |
К началу | Следующая глава |