755 Даны действительные числа х, ε (x ≠ 0, ε > 0).
Вычислить с точностью ε:
756 Даны действительные числа х, a, ε (ε > 0, |x| < 1). Вычислить с точностью ε значение
757 Даны целое число n,действительные числа х, ε (ε > 0, n ≥ 0). Вычислить с точностью ε значение
758 Дано действительное число х. Вычислить с точностью 10-6:
759 Даны действительные числа х, ε (x ≠ 0, ε > 0). Вычислить с точностью ε бесконечную сумму и указать количество учтённых слагаемых:
760 Дано действительное число х. Последовательность a1, a2, ... образована по следующему закону:
761 Дано действительное число ε (ε > 0). Вычислить
762 Дано действительное число ε (ε > 0). Последовательность a1, a2, ... образована по следующему закону:
763 Даны действительные числа х, ε (ε > 0). Последовательность a1, a2, ... образована по следующему закону: a1 = x; далее,для n = 2,3,...выполнено:
764 Рассмотрим последовательность do , d1, ... периметров вписанных в данную окружность иногоугольников с удваивающимся числом сторон. Радиус окружности - данное действительное число r. Первый из рассматриваемых многоугольников - шестиугольник. Вычислить dn (n > 0), для которого |dn - dn-1| < 10-6.
765 Даны действительные числа х, ε (0 < x < 1, ε > 0). Вычислить с точностью значение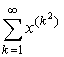 .
.
766 Даны действительные числа a, b, ε (a > b > 0, ε > 0). Последовательности x1, x2, ..., y1, y2, ... образованы по закону: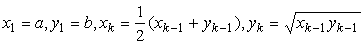 . Найти первое xn такое, что
|xn - yn| < ε.
. Найти первое xn такое, что
|xn - yn| < ε.
767 Даны действительные числа a, b. Последовательности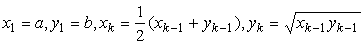 образованы по следуюшему закону: xn = a + b cos(0.5n), yn = 0.5an - b sin(0.5n).
Получить xk / yk, где k - найбольшее натуральное число, удовлетворяющее двум условиям:
k ≤ 20 µ |yk| > 10-3.
образованы по следуюшему закону: xn = a + b cos(0.5n), yn = 0.5an - b sin(0.5n).
Получить xk / yk, где k - найбольшее натуральное число, удовлетворяющее двум условиям:
k ≤ 20 µ |yk| > 10-3.
-
а)
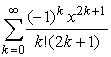
б)
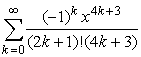
в)
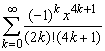
г)
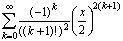
д)
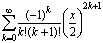
е)
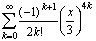
ж)
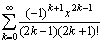
з)
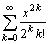
756 Даны действительные числа х, a, ε (ε > 0, |x| < 1). Вычислить с точностью ε значение
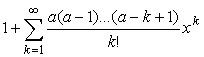 .
.
757 Даны целое число n,действительные числа х, ε (ε > 0, n ≥ 0). Вычислить с точностью ε значение
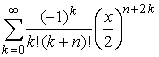 .
.
758 Дано действительное число х. Вычислить с точностью 10-6:
-
а)
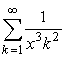
б)
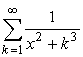
в)
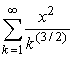
г)
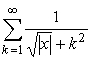
д)
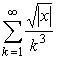
е)
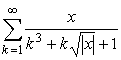
ж)
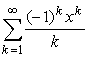
з)
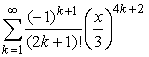 .
.
759 Даны действительные числа х, ε (x ≠ 0, ε > 0). Вычислить с точностью ε бесконечную сумму и указать количество учтённых слагаемых:
-
а)
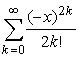
б)
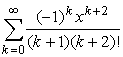
в)
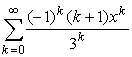
г)
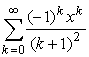
760 Дано действительное число х. Последовательность a1, a2, ... образована по следующему закону:
-
а)
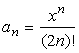
б)
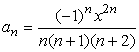
в)
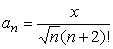
г)
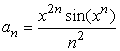
- Получить a1 + ...+ ak, где k - найменьшее число,
удовлетворяюшее двум условиям: k > 10 и |ak+1| < 10-5.
761 Дано действительное число ε (ε > 0). Вычислить
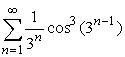
762 Дано действительное число ε (ε > 0). Последовательность a1, a2, ... образована по следующему закону:
-
а)
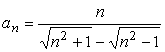
б)
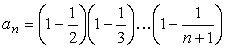
в)
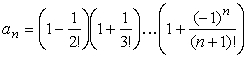
г)
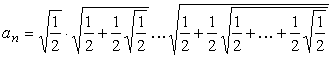
- Найти первый член an (n ≥ 2), для которого выполнено
условие |an - an-1| < ε.
763 Даны действительные числа х, ε (ε > 0). Последовательность a1, a2, ... образована по следующему закону: a1 = x; далее,для n = 2,3,...выполнено:
-
а)
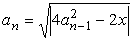 ;
;б)
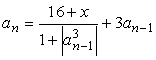 ;
;в)
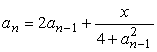 ;
;г)
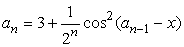 .
.
- Найти первый член an (n ≥ 2), для которого выполнено
условие
|an - an-1| < ε (ограничиться расссмотрением первых 104 членов).
764 Рассмотрим последовательность do , d1, ... периметров вписанных в данную окружность иногоугольников с удваивающимся числом сторон. Радиус окружности - данное действительное число r. Первый из рассматриваемых многоугольников - шестиугольник. Вычислить dn (n > 0), для которого |dn - dn-1| < 10-6.
765 Даны действительные числа х, ε (0 < x < 1, ε > 0). Вычислить с точностью значение
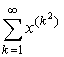 .
.766 Даны действительные числа a, b, ε (a > b > 0, ε > 0). Последовательности x1, x2, ..., y1, y2, ... образованы по закону:
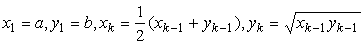 . Найти первое xn такое, что
|xn - yn| < ε.
. Найти первое xn такое, что
|xn - yn| < ε.767 Даны действительные числа a, b. Последовательности
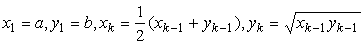 образованы по следуюшему закону: xn = a + b cos(0.5n), yn = 0.5an - b sin(0.5n).
Получить xk / yk, где k - найбольшее натуральное число, удовлетворяющее двум условиям:
k ≤ 20 µ |yk| > 10-3.
образованы по следуюшему закону: xn = a + b cos(0.5n), yn = 0.5an - b sin(0.5n).
Получить xk / yk, где k - найбольшее натуральное число, удовлетворяющее двум условиям:
k ≤ 20 µ |yk| > 10-3.
 Предыдущая глава
Предыдущая глава