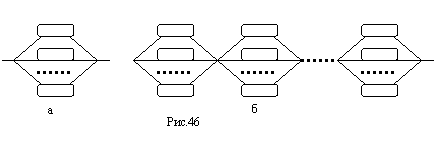
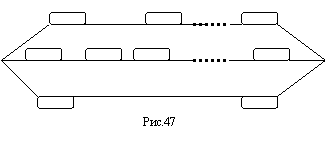
768 Группа паралельно соединённых сопротивлений изображённая на рис. 46 - а,
задаётся неотрицательными числами r1, r2, ..., ri - значениями сопротивлений.
Последовательное соединение ряда таких групп, показанное на рис. 46 - б, задаётся так: сначала идут значения
сопротивлений входящих в первую группу, затем - некоторое отрицательное число и т. д. После значения
последнего сопротивления последней группы идут два отрицательных числа Расчитать сопротивление соединения.
772 На прямой находятся три положительных заряда величины q1, q2, q3, так, как показано на рис.49. Определить расстояния от заряда q1 до точек, в которых равнодействуюшая сил отталкивания зарядами q1, q2, q3 некоторого четвёртого положительного заряда равна нулю.
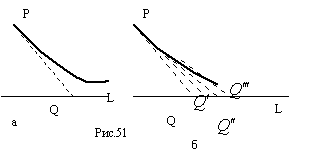
775 Вернуться к предидущей задаче. Вычислить приближённо (заменой кривой на ломанную) длину траектории собаки, расматривая первые 15с погони.
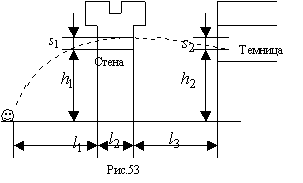
778 "Письмо Робин Гуда узнику замка Ноттингем". Письмо привязывается к камню, а камень броском посылается через боиницу стены замка в окно темницы. Расположение строений и известные величины указаны на рис.53. Рост Робин Гуда-1.6м. Можно ли забросить камень с письмом в окно? Если да, то с какой начальной скоростью и под каким углом должен бросить камень Робин Гуд? В расчетах пренебрегать сопротивлением воздуха.
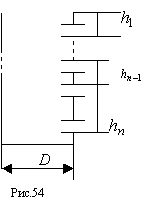
780 В стенке цилендрического ведра просверлено n маленьких отверстий, диаметр каждого из которых равен d.Остальные величины отмечены на рис.54. Известно, что nd << D. Ведро наполнено до верху водой. Необходимо определить время, за которое уровень воды в ведре опустится до нижнего отверстия. При вычислении воспользоваться тем, что скорость вытекания воды через отверстие, находашиеся на глубине x, равна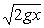 .
.
783 Ракета стартует вертикально вверх с поверхности Земли. Масса ракеты без топлива равна 10т, запас топлива М = 50т. Известно, что за каждую секунду полёта сгорает 50кг топлива. Скорость вылета из сопла частиц сгоревшего топлива постоянна относительно ракеты и сгоревшего топлива постоянна относительно ракеты и равна 104 м/с. На какой высоте окажется ракета через 100с и через 1000с полёта? Какова скорость ракеты в эти моменты? (Масса Земли равна 6 • 1021, радиус Земли - 6400км, гравитационная постоянная в законе всемирного тяготения равна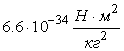 , сопротивлением воздуха пренебрегаем.) Для вычисления рассмотреть величины Mn,
hn, υn - соответственно массу неизрасходаванного топлива, высоту подъёма и
скорость движения через n секунд полёта; найти приближённые выражения Mn, hn,
υn через Mn-1, hn-1, υn-1.
, сопротивлением воздуха пренебрегаем.) Для вычисления рассмотреть величины Mn,
hn, υn - соответственно массу неизрасходаванного топлива, высоту подъёма и
скорость движения через n секунд полёта; найти приближённые выражения Mn, hn,
υn через Mn-1, hn-1, υn-1.
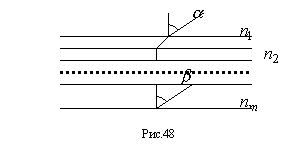
784 Имеется сферическая линза (радиус сферы R), диаметр которого равен D. Показатель преломления материала, из которого сделана линза, равен n. На расстоянии L=R/(n-1) от линзы установлен экран (рис.56,а). На линзу падает пучок паралельных лучей. Определить диаметр светового пятна на экране. Характер преломления лучей указан на рис.56,б; в этой ситуации F1.
 .
.
772 На прямой находятся три положительных заряда величины q1, q2, q3, так, как показано на рис.49. Определить расстояния от заряда q1 до точек, в которых равнодействуюшая сил отталкивания зарядами q1, q2, q3 некоторого четвёртого положительного заряда равна нулю.
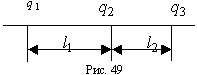
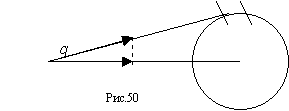
775 Вернуться к предидущей задаче. Вычислить приближённо (заменой кривой на ломанную) длину траектории собаки, расматривая первые 15с погони.
778 "Письмо Робин Гуда узнику замка Ноттингем". Письмо привязывается к камню, а камень броском посылается через боиницу стены замка в окно темницы. Расположение строений и известные величины указаны на рис.53. Рост Робин Гуда-1.6м. Можно ли забросить камень с письмом в окно? Если да, то с какой начальной скоростью и под каким углом должен бросить камень Робин Гуд? В расчетах пренебрегать сопротивлением воздуха.
780 В стенке цилендрического ведра просверлено n маленьких отверстий, диаметр каждого из которых равен d.Остальные величины отмечены на рис.54. Известно, что nd << D. Ведро наполнено до верху водой. Необходимо определить время, за которое уровень воды в ведре опустится до нижнего отверстия. При вычислении воспользоваться тем, что скорость вытекания воды через отверстие, находашиеся на глубине x, равна
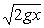 .
.
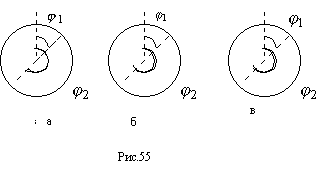
-
а) гвозди соприкосаются с обручем с внешней стороны (рис.55,б);
б) первый гвоздь соприкосается с обручем с внешней стороны, а второй - с внутренней (рис.55,в).
783 Ракета стартует вертикально вверх с поверхности Земли. Масса ракеты без топлива равна 10т, запас топлива М = 50т. Известно, что за каждую секунду полёта сгорает 50кг топлива. Скорость вылета из сопла частиц сгоревшего топлива постоянна относительно ракеты и сгоревшего топлива постоянна относительно ракеты и равна 104 м/с. На какой высоте окажется ракета через 100с и через 1000с полёта? Какова скорость ракеты в эти моменты? (Масса Земли равна 6 • 1021, радиус Земли - 6400км, гравитационная постоянная в законе всемирного тяготения равна
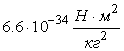 , сопротивлением воздуха пренебрегаем.) Для вычисления рассмотреть величины Mn,
hn, υn - соответственно массу неизрасходаванного топлива, высоту подъёма и
скорость движения через n секунд полёта; найти приближённые выражения Mn, hn,
υn через Mn-1, hn-1, υn-1.
, сопротивлением воздуха пренебрегаем.) Для вычисления рассмотреть величины Mn,
hn, υn - соответственно массу неизрасходаванного топлива, высоту подъёма и
скорость движения через n секунд полёта; найти приближённые выражения Mn, hn,
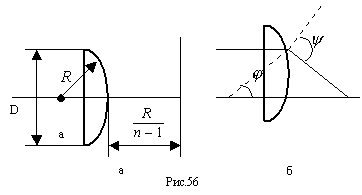
υn через Mn-1, hn-1, υn-1. 784 Имеется сферическая линза (радиус сферы R), диаметр которого равен D. Показатель преломления материала, из которого сделана линза, равен n. На расстоянии L=R/(n-1) от линзы установлен экран (рис.56,а). На линзу падает пучок паралельных лучей. Определить диаметр светового пятна на экране. Характер преломления лучей указан на рис.56,б; в этой ситуации F1.
 Предыдущая глава
Предыдущая глава