834 Чтобы зашифровать текст, записанный с помощью знаков препинания,
его можно преписать, заменить каждую букву непосредственно следующей за ней по алфавиту ( буква я заменяется на а).
835 Можно обобщить способ шифровки, изложенный в предыдущей задаче - сдвиг производится не на одну букву, а на n букв, где n - данное натуральное чило ( можно представить себе что буквы написаны по кругу, как цифры на циферблате). Выполнить задания а), б) предыдущей задачи, используя это обобщение .
836 Один из простейших способов шифровки текста состоит в табличной замене каждого символа другим символом - его шифром. Выбрать некоторую таблицу, разработать способ её представления, затем
837 Чтобы зашифровать текст из 121 буквы, его можно записать в квадратную матрицу порядка 11 по строкам, а затем прочитать по спирали, начиная с центра ( т. е. с элемента имеющего индексы 6, 6).
838 Шифровка текста с помощью решётки заключается в следующем. Решётка, т. е. квадрат из клетчатой бумаги 10 x 10 клеток, некоторые клетки в котором вырезаны, совмещается с целым квадратом 10 x 10 и через прорези на бумагу наносятся первые буквы текста. Затем решётка проворачивается на 90o и через прорези записываются следующие буквы. Это повторяется ещё дважды. Таким образом, на бумагу наносится 100 букв текста. Решётку можно изображать квадратной матрицей порядка 10 из нулей и единиц ( нуль изображает прорезь). Доказать, что матрица [ a i j ] i = 1, ..., 10; j = 1, ..., 10 может служить ключом шифра, если из элементов a i j, a 10 - i + 1 j , a i 10 - j + 1, a 10 - i + 1; 10 - j + 1 в точности один раз равен нулю.
839 Зафиксируем натуральное k и перестановку чисел 1, ..., k ( её можно задать с помощью последовательности натуральных чисел 1, ..., k). При шифровке в исходном тексте к каждой из последовательных групп по k символов применяется зафиксированная перестановка. Пусть k = 4 и перестановка есть 3, 2, 4, 1. Тогда группа cимволов s 1, s 2, s 3, s 4 заменяется на s 3, s 2, s 4, s 1.
840 Следующий способ предназначен для шифровки последовательностей нулей и единиц ( или же, например, точек и тире). Пусть a 1, ..., a n - такая последовательность. То, что предлагается в качестве её шифра, - это последовательность b 1, ..., b n, образованная по следующему закону: b1 = a1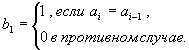
( i = 2, ..., n).
841 << Исправление ошибок >>. Пусть по некоторому каналу связи передаётся сообщение, имеющее вид последовательности нулей и единиц ( или, аналогично, точек и тире). Из - за помех возможен ошибочный прём некоторых сигналов : нуль может быть воспринят как единица и, наоборот. Можно передавать каждый сигнал трижды, заменяя, например, 1, 1, 1, 0, 0, 0, 1, 1, 1. Три последовательные цифры при расшифровке заменяются той цифрой, которая встречается среди них по крайней мере дважды. Такое утраивание сигналов существенно повышает вероятность правильного приёма сообщения.
842 Способы шифровки текста, основанные на замене входящих в него букв неокторыми символами ( см. задачу 836) или на сдвиге букв ( см. задачи 834, 835), нехороши тем, что шифр может быть разгадан путём частного анализа символов, входящих в зашифрованный текст - вспомним рассказ Э. По << Золотой жук >>. Следующий способ лишён этого недостатка. Пусть шифруемым текстом является последовательность, состоящая из буквa s 0, s 1, ..., s m. С помощью датчика случайных чисел можно, например, получать члены после довательности v 0, v 1 ... с распределением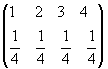 и при шифровке символа si (0 ≤ i ≤ m)
применять сдвиг на v 1, букв. Тогда две встречающиеся в зашифрованном тексте одинаковые буквы
не обязаны обозначать одну и ту же букву исходного текста. Для расшифровки сообщения нужно воспользоваться
таким же датчиком случайных чисел.
и при шифровке символа si (0 ≤ i ≤ m)
применять сдвиг на v 1, букв. Тогда две встречающиеся в зашифрованном тексте одинаковые буквы
не обязаны обозначать одну и ту же букву исходного текста. Для расшифровки сообщения нужно воспользоваться
таким же датчиком случайных чисел.
-
а) Зашифровать данный текст;
б) Расшифровать данный текст.
835 Можно обобщить способ шифровки, изложенный в предыдущей задаче - сдвиг производится не на одну букву, а на n букв, где n - данное натуральное чило ( можно представить себе что буквы написаны по кругу, как цифры на циферблате). Выполнить задания а), б) предыдущей задачи, используя это обобщение .
836 Один из простейших способов шифровки текста состоит в табличной замене каждого символа другим символом - его шифром. Выбрать некоторую таблицу, разработать способ её представления, затем
-
а) зашифровать данный текст;
б) расшифровать данный текст.
837 Чтобы зашифровать текст из 121 буквы, его можно записать в квадратную матрицу порядка 11 по строкам, а затем прочитать по спирали, начиная с центра ( т. е. с элемента имеющего индексы 6, 6).
-
а) Зашифровать данный текст.
б) Расшифровать данный текст.
838 Шифровка текста с помощью решётки заключается в следующем. Решётка, т. е. квадрат из клетчатой бумаги 10 x 10 клеток, некоторые клетки в котором вырезаны, совмещается с целым квадратом 10 x 10 и через прорези на бумагу наносятся первые буквы текста. Затем решётка проворачивается на 90o и через прорези записываются следующие буквы. Это повторяется ещё дважды. Таким образом, на бумагу наносится 100 букв текста. Решётку можно изображать квадратной матрицей порядка 10 из нулей и единиц ( нуль изображает прорезь). Доказать, что матрица [ a i j ] i = 1, ..., 10; j = 1, ..., 10 может служить ключом шифра, если из элементов a i j, a 10 - i + 1 j , a i 10 - j + 1, a 10 - i + 1; 10 - j + 1 в точности один раз равен нулю.
- Даны последовательность из 100 букв и матрица - ключ.
-
а) Зашифровать данную последовательность.
б) Расшифровать данную последовательность.
839 Зафиксируем натуральное k и перестановку чисел 1, ..., k ( её можно задать с помощью последовательности натуральных чисел 1, ..., k). При шифровке в исходном тексте к каждой из последовательных групп по k символов применяется зафиксированная перестановка. Пусть k = 4 и перестановка есть 3, 2, 4, 1. Тогда группа cимволов s 1, s 2, s 3, s 4 заменяется на s 3, s 2, s 4, s 1.
- Если в последней
группе меньше четырёх символов, то к ней добавляются пробелы. Пользуясь изложенным способом:
-
а) Зашифровать данный текст.
б) Расшифровать данный текст.
840 Следующий способ предназначен для шифровки последовательностей нулей и единиц ( или же, например, точек и тире). Пусть a 1, ..., a n - такая последовательность. То, что предлагается в качестве её шифра, - это последовательность b 1, ..., b n, образованная по следующему закону: b1 = a1
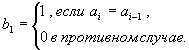
( i = 2, ..., n).
- Пользуясь изложенным способом:
-
а) Зашифровать данную последовательность.
б) Расшифровать данную последовательность.
841 << Исправление ошибок >>. Пусть по некоторому каналу связи передаётся сообщение, имеющее вид последовательности нулей и единиц ( или, аналогично, точек и тире). Из - за помех возможен ошибочный прём некоторых сигналов : нуль может быть воспринят как единица и, наоборот. Можно передавать каждый сигнал трижды, заменяя, например, 1, 1, 1, 0, 0, 0, 1, 1, 1. Три последовательные цифры при расшифровке заменяются той цифрой, которая встречается среди них по крайней мере дважды. Такое утраивание сигналов существенно повышает вероятность правильного приёма сообщения.
- Написать програму расшифровки.
842 Способы шифровки текста, основанные на замене входящих в него букв неокторыми символами ( см. задачу 836) или на сдвиге букв ( см. задачи 834, 835), нехороши тем, что шифр может быть разгадан путём частного анализа символов, входящих в зашифрованный текст - вспомним рассказ Э. По << Золотой жук >>. Следующий способ лишён этого недостатка. Пусть шифруемым текстом является последовательность, состоящая из буквa s 0, s 1, ..., s m. С помощью датчика случайных чисел можно, например, получать члены после довательности v 0, v 1 ... с распределением
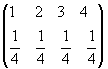 и при шифровке символа si (0 ≤ i ≤ m)
применять сдвиг на v 1, букв. Тогда две встречающиеся в зашифрованном тексте одинаковые буквы
не обязаны обозначать одну и ту же букву исходного текста. Для расшифровки сообщения нужно воспользоваться
таким же датчиком случайных чисел.
и при шифровке символа si (0 ≤ i ≤ m)
применять сдвиг на v 1, букв. Тогда две встречающиеся в зашифрованном тексте одинаковые буквы
не обязаны обозначать одну и ту же букву исходного текста. Для расшифровки сообщения нужно воспользоваться
таким же датчиком случайных чисел. - В следующих двух заданиях для
простоты предполагается, что текст записан русскими буквами без знаков препинания, пробел после шифровки
остаётся пробелом.
-
а) Зашифровать данный текст.
б) Расшифровать данный текст.
 Предыдущая глава
Предыдущая глава