933 Изобразить на экране точку,пересекающую с постоянной
скоростью экран справа налево параллельно его горизонтальной оси.
934 К условию предыдущей задачи добавляется следующее требование: как только точка доходит до левого края, в этот момент от правого края в строке, выбранной с помощью датчика случайных чисел, начинает свое движение другая точка и т. д. Цвет точки также может выбираться с помощью датчика случайных чисел.
935 Усложним условие предыдущей задачи: очередная точка начинает движение от правого края экрана несколько раньше, чем предыдущая точка доходит до левого края.Попытаться добитиься того,чтобы одновременно на экране двигались три,четыре точки.
936 Изобразить на экране точку, движущуюся по окружности с постоянной угловой скоростью.
937 Составить программу для управления скоростью движения точки по окружности (см.предыдущую задачу). Управление производится клавишами ">" (скорость несколько увеличивается) и "<" (скорость несколько уменьшается).
938 Изобразить на экране прямую, вращающуюся в плоскости экрана вокруг одной из своих точек. Задачу можно усложнить дополнительным требованием, чтобы цвет прямой изменялся при переходе от предыдущего положения к следующему.
939 Изобразить на экране отрезок, вращающийся в плоскости экрана вокруг:
940 Усложним условие задачи 938: в плоскости экрана должны вращаться, каждая вокруг своей точки, две прямые.
941 В условие предыдущей задачи вносится дополнение: должна быть предоставлена возможность управления с клавиатуры расстоянием между центрами вращения.
942 Изобразить на экране две движущиеся точки, траектории которых являются концентрическими окружностями. Угловаяя скорость точки, движущейся по внутренней окружности, должнаа быть несколько меньше, чем угловая скорость точки, движущейся повнешней окружности (обе скорости - постоянные величины). При этом
943 Изобразить одновременное вращение двух сстрелок - большой и малой, при котором одному полному обороту большой стрелки соответствует 1/12 оборота малой стрелки (как на циферблате часов). Стрелки можно для простоты заменить отрезками.
944 Изобразить на экране правильный треугольник, вращающийся в плоскости экрана вокруг своего центра.
945 Изобразить на экране разносторонний треугольник, вращающийся в плоскости экрана вокруг свооего центра тяжести.
946 Изобразить на экране прямоуугольник, вращающийся в плоскости экрана вокруг своего центра.
947 Изобразить наэкране прямоугольник, вращающийся в плоскости экрана вокруг одной изсвоих вершин.
948 Условия задач 938, 939,944-947 изменяются следующим образом: во время вращения прямой, отрезка или многоугольника центр вращения с постоянной скоростью перемещается от одного края экрана до другого параллельно горизонтальной оси экрана.
949 Условие этой задачи отличается от предыдущей тем, что требуется сохранять на экране все высвеченные положения геометрической фигуры. Задачу можно еще усложнить дополнительным требованием, чтобы цвет фигуры изменился при переходе от предыдущего положения к следующему.
950 Изобразить движущуюся прямую, которая в каждый момент касается окружности данного радиуса, центр которой совпадает с центром экрана.Точка касания перемещается по окружности с постоянной угловой скоростью. Сама окружность невидима.
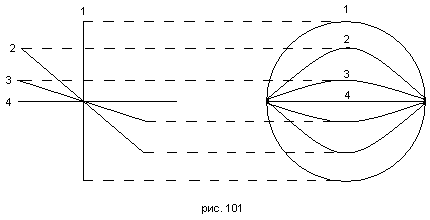
951 Круглое кольцо вращается с постоянной угловой скоростью вокруг своего диаметра, расположенного параллельно горизонтальной оси экрана. Изобразить на экране процесс вращения. Считать, что в момент времени t кольцо выглядит для наблюдателя как элипс, большая ось которого равна постоянной величине с, а малая равна с|cos φ t|, где φ - угловая скорость вращения. Вправой части Рис. 101 приведено несколько последовательных изображений. В левой части рисунка кольцо изображено сбоку (этот вид не даётся на экране).
953 Изобразить на экране гармонические колебания точки вдоль некоторого горизонтального отрезка. Если длина отрезка равна с, то расстояние от точки до левого конца в момент времени t можно считать равным с(1+cosφ t)/2, где -некоторая постоянная. Предусмотреть возможность управления частотой колебания с помощью клавиш ">" и "<", аналогично тому, как это описано в задаче 937 в отношении вращающейся точки. С помощью двух других клавиш можно управлють амплитудой, т. е. величиной с.
954 Изобразить точку, совершающую независимые гармонические колебания с частотой φ1, по горизонтали и с частотой φ2 по вертикали (амплитуда тех и других колебаний равна а). Считать, что в момент времени t точка имеет координаты x=a cosx*φ1(t-t1), y=a cosφ2(t-t2); числа t1 и t2даны. Предусмотреть возможность управления с клавиатуры значениями φ1 и φ2.
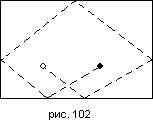
955 Изобразить на экране движение шара по биллиарду без луз (рис. 102).
957 Изобразить на экране точку, пересекающую экран равноускореено в вертикальном направлении.
958 Выполнить задачи 934, 935 применительно к равноускоренному движению.
959 Изобразить на экране приближающийся издали шар. По какому закону возрастает видимый диаметр шара с течением времени?
960 Согласно первому и второму закону Каплера, каждая планета движется по элипсу, в одном из фокусов которого находится Солнце. В равные времена радиус-вектор вектор планеты, проведённый от оси Солнца, заметает равные площади (рис. 103, а). Если ввести в плоскости орбиты полярные координаты так, как показано на рис. 103, б (Солнце выбирается в качестве полюса), то дифференциальным уравнением движения планеты будет
Получить на экране картину, дающую модель движения планеты вокруг Солнца (планета и Солнцё изображаются свтящимися точками: Солнце - неподвижной, а планета - подвижной). Для нахождения последовательностей φ0, φ1, ..., ρ0, ρ1,... значений угла φ и расстояния ρ через одигаковые промежутки времени, равные τ, можно воспользоваться методом Эйлера численного решения дифференциальных уравнений. Это позволит написать
Значения c, τ, p, e следует подобрать так, чтобы картина на экране получилась достаточно выразительной (хотя, строго говоря, величины c, р и е не могут выбираться независимо друг от друга: они связаны соотношениями, вытекающими, в частности, из третьего закона Кеплера, но в данной графической задаче этим можно пренебречь). Для того, чтобы представить себе форму элипса в зависимости от р и е, рекомендуется рассмотреть случаи φ = 0, π/2, π.
962 Получить на экране слово ТЕСТ, составленное из крупных букв так, как описано в задаче 893, и обеспечить его перемещение по экрану:
963 Аналогично предыдущей задаче получить на экркне два слова ТЕСТ, движущиеся по экрану по одной горизонтальной прямой на встречу друг другу. Первое слово должно двигаться от левого края экрана к правому, второе - от правого к левому. Движение должно выполнятся до полного совмещения слов.
964 Получить на экране какую-либо фигуру, описанную в задаче 129 (рис. 11,а - 11,о), и "оживить" её: пусть цыплёнок (рис 11, а) летает, из трубы домика (рис. 11, б) идёт дым, грузовик (рис. 11, в) едет, елка (рис. 11, г) растёт, шар (рис. 11, д) движется влево до соприкоснавения со стенкой и обратно, треугольник (рис. 11, е) движется вниз до соприкосновения с нижней фигурой, рожица (рис. 11, ж) подмигивает, рыба (рис. 11, з) плывёт, подводная лодка (рис. 11, и) поднимает и опускает перископ, сова (рис. 11, к) машет крыльями, стрелки будильника (рис. 11, л) и колесо (рис. 11, н) вращаются, велосипед (рис. 11, м) катится, телефонный диск (рис. 11, о) крутится.
965 Получить на экране изображение какой-либо фигуры, описанной в задаче 130, и обеспечить её перемещение (шаблоны для построения фигур даны на рис. 12, а - 12, р). Выбор направления перемещения и расстояния, на которое фигура должна перемещатся в данном направлении, выполнять:
966 Получить звуковой мультфильм "Танцующий НЛО". НЛО строить из отдельных символов так, как показано на рис. 104. Очередное положение НЛО на эране определять с помощью датчика случайных чисел. Результатом обращения к датчику случайных чисел должны быть номера строки и столбца экрана, с которыми следует совместить левый верхний угол прямоугольника размером 3 X 4 символа, объемлющего НЛО. Каждый раз, когда номер полученного таким образом столбца окажется кратным 12, НЛО должен издавать звуковой сигнал.
969 Получить звуковой фильм "Человек, танцующий под музыку". Танец может заключаться в выполнении самых простых движений, например, притоптываний ногой или приседании, в такт мелодии, воспроизводимой по звукогенератору.
970 Аналогично предыдущей задаче получить звуковой мультфильм "Человек, играющий на гитаре". Игра на гитаре может изображаться, например с помощью перемещения правой руки по струнам гитары вверх и вниз. Мультфильм должен сопровождаться воспроизведением популярной медодии.
971 Изобразить на экране доску Гальтона (см. задачу 751) с движущимися по ней шариками. Одновременно по доске должно двигаться несколько шариков. Закончившие движение шарики остаются в нижней части доски. Использовать датчик случайных чисел для выбора пути шарика при прохождении через препятствие.
934 К условию предыдущей задачи добавляется следующее требование: как только точка доходит до левого края, в этот момент от правого края в строке, выбранной с помощью датчика случайных чисел, начинает свое движение другая точка и т. д. Цвет точки также может выбираться с помощью датчика случайных чисел.
935 Усложним условие предыдущей задачи: очередная точка начинает движение от правого края экрана несколько раньше, чем предыдущая точка доходит до левого края.Попытаться добитиься того,чтобы одновременно на экране двигались три,четыре точки.
936 Изобразить на экране точку, движущуюся по окружности с постоянной угловой скоростью.
937 Составить программу для управления скоростью движения точки по окружности (см.предыдущую задачу). Управление производится клавишами ">" (скорость несколько увеличивается) и "<" (скорость несколько уменьшается).
938 Изобразить на экране прямую, вращающуюся в плоскости экрана вокруг одной из своих точек. Задачу можно усложнить дополнительным требованием, чтобы цвет прямой изменялся при переходе от предыдущего положения к следующему.
939 Изобразить на экране отрезок, вращающийся в плоскости экрана вокруг:
-
а)своей середины;
б)своего конца;
в)точки, делящей отрезок в отношении 1:3.
940 Усложним условие задачи 938: в плоскости экрана должны вращаться, каждая вокруг своей точки, две прямые.
941 В условие предыдущей задачи вносится дополнение: должна быть предоставлена возможность управления с клавиатуры расстоянием между центрами вращения.
942 Изобразить на экране две движущиеся точки, траектории которых являются концентрическими окружностями. Угловаяя скорость точки, движущейся по внутренней окружности, должнаа быть несколько меньше, чем угловая скорость точки, движущейся повнешней окружности (обе скорости - постоянные величины). При этом
-
а) обе точки вращаются в одном направлении (например, по часовой стрелке);
б) точки вращаются в противоположных направлениях.
943 Изобразить одновременное вращение двух сстрелок - большой и малой, при котором одному полному обороту большой стрелки соответствует 1/12 оборота малой стрелки (как на циферблате часов). Стрелки можно для простоты заменить отрезками.
944 Изобразить на экране правильный треугольник, вращающийся в плоскости экрана вокруг своего центра.
945 Изобразить на экране разносторонний треугольник, вращающийся в плоскости экрана вокруг свооего центра тяжести.
946 Изобразить на экране прямоуугольник, вращающийся в плоскости экрана вокруг своего центра.
947 Изобразить наэкране прямоугольник, вращающийся в плоскости экрана вокруг одной изсвоих вершин.
948 Условия задач 938, 939,944-947 изменяются следующим образом: во время вращения прямой, отрезка или многоугольника центр вращения с постоянной скоростью перемещается от одного края экрана до другого параллельно горизонтальной оси экрана.
949 Условие этой задачи отличается от предыдущей тем, что требуется сохранять на экране все высвеченные положения геометрической фигуры. Задачу можно еще усложнить дополнительным требованием, чтобы цвет фигуры изменился при переходе от предыдущего положения к следующему.
950 Изобразить движущуюся прямую, которая в каждый момент касается окружности данного радиуса, центр которой совпадает с центром экрана.Точка касания перемещается по окружности с постоянной угловой скоростью. Сама окружность невидима.
951 Круглое кольцо вращается с постоянной угловой скоростью вокруг своего диаметра, расположенного параллельно горизонтальной оси экрана. Изобразить на экране процесс вращения. Считать, что в момент времени t кольцо выглядит для наблюдателя как элипс, большая ось которого равна постоянной величине с, а малая равна с|cos φ t|, где φ - угловая скорость вращения. Вправой части Рис. 101 приведено несколько последовательных изображений. В левой части рисунка кольцо изображено сбоку (этот вид не даётся на экране).
953 Изобразить на экране гармонические колебания точки вдоль некоторого горизонтального отрезка. Если длина отрезка равна с, то расстояние от точки до левого конца в момент времени t можно считать равным с(1+cosφ t)/2, где -некоторая постоянная. Предусмотреть возможность управления частотой колебания с помощью клавиш ">" и "<", аналогично тому, как это описано в задаче 937 в отношении вращающейся точки. С помощью двух других клавиш можно управлють амплитудой, т. е. величиной с.
954 Изобразить точку, совершающую независимые гармонические колебания с частотой φ1, по горизонтали и с частотой φ2 по вертикали (амплитуда тех и других колебаний равна а). Считать, что в момент времени t точка имеет координаты x=a cosx*φ1(t-t1), y=a cosφ2(t-t2); числа t1 и t2даны. Предусмотреть возможность управления с клавиатуры значениями φ1 и φ2.
955 Изобразить на экране движение шара по биллиарду без луз (рис. 102).
957 Изобразить на экране точку, пересекающую экран равноускореено в вертикальном направлении.
958 Выполнить задачи 934, 935 применительно к равноускоренному движению.
959 Изобразить на экране приближающийся издали шар. По какому закону возрастает видимый диаметр шара с течением времени?
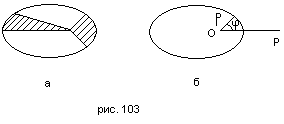
960 Согласно первому и второму закону Каплера, каждая планета движется по элипсу, в одном из фокусов которого находится Солнце. В равные времена радиус-вектор вектор планеты, проведённый от оси Солнца, заметает равные площади (рис. 103, а). Если ввести в плоскости орбиты полярные координаты так, как показано на рис. 103, б (Солнце выбирается в качестве полюса), то дифференциальным уравнением движения планеты будет
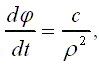
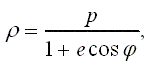
Получить на экране картину, дающую модель движения планеты вокруг Солнца (планета и Солнцё изображаются свтящимися точками: Солнце - неподвижной, а планета - подвижной). Для нахождения последовательностей φ0, φ1, ..., ρ0, ρ1,... значений угла φ и расстояния ρ через одигаковые промежутки времени, равные τ, можно воспользоваться методом Эйлера численного решения дифференциальных уравнений. Это позволит написать
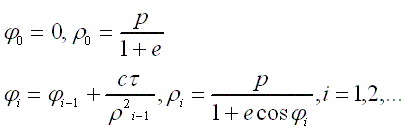
Значения c, τ, p, e следует подобрать так, чтобы картина на экране получилась достаточно выразительной (хотя, строго говоря, величины c, р и е не могут выбираться независимо друг от друга: они связаны соотношениями, вытекающими, в частности, из третьего закона Кеплера, но в данной графической задаче этим можно пренебречь). Для того, чтобы представить себе форму элипса в зависимости от р и е, рекомендуется рассмотреть случаи φ = 0, π/2, π.
962 Получить на экране слово ТЕСТ, составленное из крупных букв так, как описано в задаче 893, и обеспечить его перемещение по экрану:
-
а) по горизонтали от левого края экрана к правому краю;
б) по вертикали от верхнего края экрана к нижнему и обратно.
963 Аналогично предыдущей задаче получить на экркне два слова ТЕСТ, движущиеся по экрану по одной горизонтальной прямой на встречу друг другу. Первое слово должно двигаться от левого края экрана к правому, второе - от правого к левому. Движение должно выполнятся до полного совмещения слов.
964 Получить на экране какую-либо фигуру, описанную в задаче 129 (рис. 11,а - 11,о), и "оживить" её: пусть цыплёнок (рис 11, а) летает, из трубы домика (рис. 11, б) идёт дым, грузовик (рис. 11, в) едет, елка (рис. 11, г) растёт, шар (рис. 11, д) движется влево до соприкоснавения со стенкой и обратно, треугольник (рис. 11, е) движется вниз до соприкосновения с нижней фигурой, рожица (рис. 11, ж) подмигивает, рыба (рис. 11, з) плывёт, подводная лодка (рис. 11, и) поднимает и опускает перископ, сова (рис. 11, к) машет крыльями, стрелки будильника (рис. 11, л) и колесо (рис. 11, н) вращаются, велосипед (рис. 11, м) катится, телефонный диск (рис. 11, о) крутится.
965 Получить на экране изображение какой-либо фигуры, описанной в задаче 130, и обеспечить её перемещение (шаблоны для построения фигур даны на рис. 12, а - 12, р). Выбор направления перемещения и расстояния, на которое фигура должна перемещатся в данном направлении, выполнять:
-
а) с помощью датчика случайных чисел;
б) под управлением с клавиатуры - для этого должны использоваться клавиши "стрелка вверх", "стрелка вниз", "стрелка вправо", "стрелка влево", вызывающие перемещение фигуры в соответствующем направлении на 5 пиксел.
966 Получить звуковой мультфильм "Танцующий НЛО". НЛО строить из отдельных символов так, как показано на рис. 104. Очередное положение НЛО на эране определять с помощью датчика случайных чисел. Результатом обращения к датчику случайных чисел должны быть номера строки и столбца экрана, с которыми следует совместить левый верхний угол прямоугольника размером 3 X 4 символа, объемлющего НЛО. Каждый раз, когда номер полученного таким образом столбца окажется кратным 12, НЛО должен издавать звуковой сигнал.
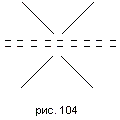
-
а) идущего человека;
б) бегущего человека;
в) человека, выполняющего приседания;
г) человека, выполняющего сигнализацию флажком.
-
а) о метании диска;
б) о беге с барьерами;
в) о подтягивании на перекладине;
г) о прыжках в длину;
д) о гребле;
е) о поднятии штанги.
969 Получить звуковой фильм "Человек, танцующий под музыку". Танец может заключаться в выполнении самых простых движений, например, притоптываний ногой или приседании, в такт мелодии, воспроизводимой по звукогенератору.
970 Аналогично предыдущей задаче получить звуковой мультфильм "Человек, играющий на гитаре". Игра на гитаре может изображаться, например с помощью перемещения правой руки по струнам гитары вверх и вниз. Мультфильм должен сопровождаться воспроизведением популярной медодии.
971 Изобразить на экране доску Гальтона (см. задачу 751) с движущимися по ней шариками. Одновременно по доске должно двигаться несколько шариков. Закончившие движение шарики остаются в нижней части доски. Использовать датчик случайных чисел для выбора пути шарика при прохождении через препятствие.
 Предыдущая глава
Предыдущая глава