1014 Магическим квадратом порядка л называется квадратная таблица размера n х n, составленная из чисел 1,2, ..., n2 так, что суммы по каждому столбцу, каждой строке и каждой из двух диагоналей равны между собой. Дана целочисленная квадратная матрица порядка 5; определить, является ли она магическим квадратом.
1015 Латинским квадратом порядка п называется квадратная таблица размера n х n,. каждая строка и каждый столбец которой содержит числа 1, 2, ..., n. Дана целочисленная квадратная матрица порядка 5; определить, является ли она латинским квадратом.
1016 Дана целочисленная матрица [aij]i=1,...n;j=1,...,m, каждый элемент которой равен 0, 1,2 или 3. Определить количество четверок аij, аi+1, aij+i, ai+1 j+1, в каждой из которых все элементы различны.
1017 Даны целые числа а1, ..., аn. Определить, является ли эта последовательность периодической (т. е. может ли она быть получена повторениями некоторой своей начальной части). Из всех периодов указать наименьший.
1018 Даны действительные числа а1, ..., аn. Найти самый длинный отрезок аp, ap+1, ..., аp+m данной последовательности, элементы которого удовлетворяют соотношениям аn < ap+1 > аp+2 < ... > аp+m.
1019 Даны целые числа a1, ..., an. Является ли последовательность a1, ..., аn перестановкой чисел 1, ..., n?
1020 Элемент матрицы называется седловой точкой, если он является одновременно наименьшим в своей строке и наибольшим в своем столбце. Дана действительная матрица размера 5х6. Выяснить, имеются ли седловые точки в этой матрице, и если имеются, то указать индексы одной из них.
1021 Известна игра на придумывание слов, состоящих из тех же букв, что и некоторое фиксированное слово - образец. Например, из слова ПАСКАЛЬ можно получить слова ЛАК, ЛАСКА, СКАЛА и т. д. Кратные вхождения некоторой буквы в получаемое слово допускаются, если эта буква с неменьшей кратностью входит в слово - образец. Пусть дана последовательность слов, разделенных пробелами. Приняв, что первое слово в последовательности есть образец, выбрать те из остальных членов последовательности, которые могут быть получены из образца по указанному выше правилу. Максимально возможную длину слова считать равной 15.
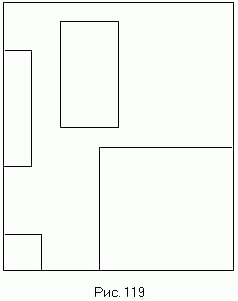
1022 На квадратном листе клетчатой бумаги размера 8х8 клеток нарисовано несколько прямоугольников, каждый прямоугольник состоит из клеток, различные прямоугольники не накладываются друг на друга и не соприкасаются (см. пример на рис. 119). Дана целочисленная квадратная матрица порядка 8, в которой элемент равен О, если соответствующая клетка принадлежит какому - либо прямоугольнику, и отличен от нуля в противном случае. Определить число прямоугольников.
1023 Дана целочисленная матрица [аij]i=1,..., n; j=1,..., m. Прямоугольником в этой матрице будем называть множество всех элементов аij, для которых выполнено 1≤p≤i≤q≤n, 1≤r≤s≤m, где р, q, г, s - натуральные числа, задающие прямоугольник. Площадью прямоугольника назовем число элементов в нем. Среди прямоугольников матрицы, состоящих целиком из нулей, найти тот, который имеет наибольшую площадь.
1024 Дана целочисленная матрица размера nхm, в которой имеются ровно два одинаковых элемента. Найти индексы этих элементов.
1025 Поле шахматной доски задается парой натуральных чисел; первое указывает номер вертикали при счете слева направо, второе - номер горизонтали при счете снизу вверх. Расстановка фигур задается таким образом, что вначале указываются поля, на которых стоят перечисленные белые фигуры, затем - поля, на которых стоят перечисленные черные фигуры.
-
а) На доске стоят два ферзя. Указать поля, на которые может пойти белый ферзь так, чтобы не
попасть под удар черного ферзя.
б) У белых на доске остался только король, у черных - король, конь, слон. Охарактеризовать положение белых с помощью слов: мат, шах, пат, обыкновенная позиция.
1026 "Тестирование коллектива". Пусть целочисленная матрица размера n х m содержит информацию об учениках некоторого класса из n человек: j-я строка содержит информацию о i-м ученике. В первом столбце проставлен возраст в годах, во втором - рост в см, в третьем - успеваемость (округленный средний балл) и т. д. Ученик называется среднестатистическим по k-му параметру (уникальным по k-му параметру), если на нем достигается минимум (максимум) модуля разности среднего арифметического чисел из k-го столбца и значения k-го параметра этого ученика. Ученик называется самым уникальным (самым средним), если он уникален (является среднестатистическим) по самому большому количеству параметров. По матрице указанного вида определить номера учеников:
-
а) самых уникальных;
б) самых средних;
в) самых средних среди самых уникальных;
г) самых уникальных среди самых средних.
1027 Правильное скобочное выражение получается из некоторого математического выражения, содержащего круглые скобки, вычеркиванием всех знаков, кроме круглых скобок. Например, из выражения а-b(c+2(x+y(z+1)))+а(с+х) получается правильное скобочное выражение ((( )))( ). Более точное описание множества правильных скобочных выражений:
-
1) ( )-правильное скобочное выражение;
2) если Р - правильное скобочное выражение, то (Р)- правильное скобочное выражение;
3) если Р и Q - правильные скобочные выражения, то pQ - правильное скобочное выражение.
 Предыдущая глава
Предыдущая глава