178 Даны натуральные числа n, a 1...an.
Определить количество членов ak последовательности a1,...,an:
179 Данные натуральные числа n,q1,...,qn. найти те члены qi последовательности q1,...,qn, которые
180 Дано натуральное число n. Получить сумму тех чисел вида i3 -3in2 + n (i = 1,2,...,n), которые явлются утроенными нечетными.(*)
181 Даны целые числа a1,...a50. Получить сумму тех чисел данной последовательности, которые
182 Даны натуральное число n, целые часла a1,...,an. Найти количество и сумму тех членов данной последовательности, которые делятся на 5 и не делятся на 7.
183 Даны натуральные числа n, p, целые числа a1,...,an. Получить произведение членов последовательности a1,...,an, кратных p.
184 Даны целые числа p, q, a1,...,a67 (p > q ≥ 0). В последовательности a1, ..., a67 заменить нулями члены, модуль которых при делении на p дает в остатке q.
185 Даны натуральное число n, действительные числа a1,...,an. Получить удвоенную сумму всех положительных членов последовательности a 1,...,an.
186 Даны натуральное число n, действительные числа a1,...,an. Вычислить обратную величину произведения тех членов ai последовательности a1,..., an, для которых выполнено i+1<ai<i!.
187 Даны натуральное число n,действительные числа a1,..., an. В последовательности a1,...,an все отрицательные члены увеличить на 0.5, а все неотрицательные заменить на 0.1.
188 Даны натуральное число n, действительные числа x1,..., xn. В последовательности x1,..., xn все члены, меньшие двух, заменить нулями. Кроме того, получить сумму членов, принадлежащих отрезку [3,7], а также число таких членов.
189 Даны натурльное число n, действительные числа a1 ,...,an. В последовательности a1 ,...,an все неотрицательные члены, не принадлежащие отрезку [1,2], заменить на единицу. Кроме того, получить число отрицательных членов и число членов, принадлежащих отрезку [1,2].
190 Даны натеральное число n, целые числа a1,...,an. Получить сумму положительных и число отрицательных членов последовательности a1,...,an.
191 Даны натуральное число n, целые числа a1,...,an. Заменить все большие семи члены последовательности a1,...,an числом 7. Вычислить количество таких членов.
192 Даны целые числа a1,...,a45. Получить число отрицательных членов последовательности a1,...,a35 и число нулевых членов всей последовательности a1,...,a45.
193 Пусть xо = a; xk = qxk-1+b (k = 1,2,...). Даны неотрицательное целое n, действительные a, b, c, d, q (c<d). Пренадлежит ли xn интервалу (c, d)?
194 Даны натуральнее число n, целые числа а, х1 , ..., хn. Если в последовательности х1 , ..., хn есть хотя бы один член, равный а, то получить сумму всех членов, следующих за первым таким членом; в противном случае ответом должно быть число -10.
195 Даны натуральное число n, действительные числа а, b, c1 , ..., cn. Верно ли(**), что при 1 ≤ k ≤ n-1 всякий раз, когда ck < a, выполнено ck+l > b?
196 Даны целые числа a1,...,a50. Получить последовательность b1,...,b50, которая отличается от исходной тем, что все нечётные члены удвоны.
197 Вычислить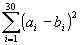
, где
198 Даны натуральные числа n, b0,...,bn. Вычислить f (b0) + f (b1) +...+ f (bn), где
199 Даны натуральное число n, действительные числа r, a1,...,an (n ≥ 2). Сколько среди точек (a1, an), (a2, an-1),..., (an, a1) таких, которые принадлежат кругу радиуса r с центром в начале координат?
200 Даны целые числа a, n, x1,...,xn(n > 0). Определить, каким по счету идёт в последовательности x1,...,xn член, равный a. Если такого члена нет, то ответом должно быть число 0.
201 Даны натуральное число n, действительные числа a1,...,an. Получить:
202 Даны натуральное число n, действительные числа a1,...,an.
203 У прилавка в магазине выстроилась очередь из n покупателей. Время обслуживания продавцом i-го покупателя равно ti (i = 1,...,n). Пусть даны натуральное n и действительные t1,...,tn. Получить c1,...,cn, где ci - время прибывания i-го покупателя в очереди (i = 1,...,n). Указать номер покупателя, для обслуживания которого продавцу потребовалось самое малое время.
204 В некоторых видах спортивных состязаний выступление каждого спортсмена независимо оценивается несколькими судьями, затем из всей совокупности оценок удаляются наибдолее высокая и наиболее низкая, а для оставшихся оценок вычисляется среднее арифметическое, которое и идет в зачет спортсмену. Если наиболее высокую оценку выставило несколько судей, то из совокупности оценок удаляется только одна такая оценка; аналогично поступают с наиболее низкими оценками.
205 Даны натуральное число n, действительные числа a1,...,an. Получить max (|a1|,...,|an|) и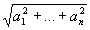
.
206 Дано натуральное число n. Найти наибольшее среди чисел kesin2(k+1) (k = 1,...,n), а также сумму всех этих чисел.
207 Дано натуральное число n. Выбросить из записи числа n цифры 0 и 5, оставив прежним порядок остальных цифр. Например, из числа 59015509 должно получиться 919.
208 Даны натеральное число n, целые числа a1,...,an.Найти:
209 Даны натуральное число n, действительное число x. Среди чисел ecos(x2k)sin(x3k) (k = 1,...,n) найти ближайшее к какому - нибудь целому.
210 Даны натуральное число n, действительные числа a1,...,an. Получить все натуральные j (2 ≤ j ≤ n-1), для которых aj-1 < aj > aj+1.
211 Пусть x1 = 0.3; x2 = -0.3; xi = i + sin(xi-2), i=3,4,... Среди x1,...,x100 найти ближайшее к какому - нибудь целому.
212 Пусть x1 = y1 = 1;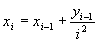
;
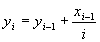, i = 2, 3.... Получить x8, y18.
213 Пусть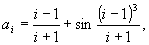
, i=1,2,...
Дано натуральное n. Среди a1,...,an найти все положительные числа, среди положительных a1,...,an выбрать наименьшее число.
214 Пусть ao = cos21; a1 = - sin21; ak = 2ak-1 - ak-2, k = 2,3,...
215 Даны натуральное число n, действительные числа a1,...,an. В последовательности a1,...,an, определить число соседств:
216 Даны целые числа c1,...,c95. Имеются ли в последовательности c1,...,c95:
217 Даны натуральное число n, действительные числа x1,...,x3n. Последовательность чисел x1,...,x3n определяет на плоскости n квадратов со сторонами, параллельными координатным осям: так, x1, x2 - координаты центра первого квадрата, x3 - длина его стороны; аналогично, числа x4, x5, x6 определяют второй квадрат, x7, x8, x9 - третий и т.д. Имеются ли точки, принадлежащие всем квадратам? Если да, то указать координаты одной из них.
218 Даны натуральное число n, действительные числа x1,...,x3n. Вычислить сумму из xn+1,...,x3n, которые превосходят по величине все числа x1,...,xn.
219 Даны действительные числа a,b (a < b), натуральное число n, функция y = f(x) , определенная на отрезке [a,b]. Для значений аргумента xi=a+ih (i=0,1,...,n), h = (b-a)/n вычислить значения функции yi = f(xi)(i=0,1,..,n).
220 Рассматривается последовательность a1,...,a1000. Требуется определить, сколько членов последовательности с номерами 1,2,4,8,16,... имеют значение, меньшее, чем 0.25. При этом считать, что
221 Даны натуральное число n, действительные числа x1,...,xn. Получить (1+r)/(1+s), где r - сумма всех трех членов последовательности x1,...,xn, которые не превосходят 1, а s - сумма членов, больших 1.
222 Даны натуральное число n, действительные числа y1,..., yn. Найти:
223 Даны целые числа a1,a2,... Известно, что a1 > 0 и что среди a2,a3,... есть хотябы одно отрицательное число. Пусть a1,..., an - члены данной последовательности, предшествующие первому отрицательному члену (n заранее неизвестно). Получить:
224 Дано натуральное число n. Получить все его натуральные делители.
225 Дано натуральное число n. Получить все такие натуральные q, что n делится на q2 и не делится на q3.
226 Даны натуральные числа m, n. Получить все их натуральные общие кратные, меньшие mn.
227 Даны целые числа m, n (m ≠ 0, n ≠ 0). Получить все их общие делители (положительные и отрицательные).
228 Даны натуральное число n, действительные числа a1,..., an. Выяснить, является ли последовательность a1,...,an упорядоченной по убыванию.
229 Даны действительные числа x, y (x >0, y >1). Получить целое число k (пложительное, отрицательное или равное нулю), удовлетворяющее условию yk-1 ≤ x < yk.
230 Даны натуральное число n, действительные числа a1,..., an. Найти длину наименьшего отрезка числовой оси, содержащего числа a1,..., an.
231 Даны действительные числа x, y1,...,y12. Выяснить, во-первых, верно ли, что y1 ≤ x ≤ y12 и, во-вторых, верно ли, что t1 ≤ x ≤ t2, где t1 - наименьшее, а t2 - наибольшее среди y1,...,y12. (Какие комбинации ответов на первый и второй вопросы возможны?)
232 Даны натуральное число n, действительные числа a, x1,..., xn (x1 ≤ x2 ≤ ... ≤ xn). Получить последовательность y1,...,yn+1, членами которой являются члены последовательности x1,...,xn и значение a, такую, что y1 ≤ y2 ≤ ... ≤ yn+1.
233 Даны натуральное число n, целые числа a1,..., an. Оставить без изменения последовательность a1,...,an, если её члены упорядочены по неубыванию или по невозрастанию. В противном случае получить подпоследовательность a1,...,am(m < n), где m таково, что либо a1 ≤ a2 ≤ ... ≤ am и am > am+1, либо a1 ≥ a2 ≥ ... ≥ am и am < am+1.
234 Даны натуральное число n, действительные числа x1,..., xn. Получить в порядке следования все xk, удовлетворяющие неравенствам xk > x1, xk > x2,...,xk > xk-1.
235 Даны натуральные числа m и n. Получить: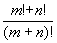
236 Даны натуральное число n, действительное число x. Получить: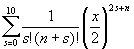
237 Даны натуральное число n, действительное число r.
238 Дано натуральное число n. Вычислить произведение первых n сомножителей
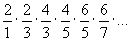
239 Дано натуральное число n. Вычислить
.
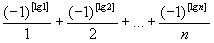240 Для любого целого k обозначим количество цифр в его десятичной записи через Ц(k).
241 Дано натуральное число n, действительное число x. Вычислить
.
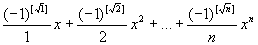242 Дано натуральное число n. Вычислить
243 Дано натуральное число n. Можно ли представить его в виде суммы двух квадратов натуральных чисел? Если можно, то
244 Даны натуральное число n, целые числа a1,...,an.
245 Даны натуральное число n, целые числа a1,..., a30, b1,...,b40, c1,...,cn. Верно ли, что отрицательный член в последовательности c1,...,cn встречается раньше, чем в последовательностях a1,...,a30 и b1,..., b40? Предпологается, что каждая из последовательностей содержит хотя бы один отрицательный член.
246 Даны натуральное число n, действительные числа a1,..., an. Выяснить, образуют ли возрастающую последовательность числа:
247 Даны натуральные числа n, x0 , y0 , r, x1, y1 ,..., xn, yn. Построить на экране точки с координатами xi, yi:
248 Даны натуральные числа n, x1, y1, x2, y2 ,..., xn, yn. Построить на экране точки с координатами xi, yi:
249 Даны натуральные числа n, x1 , y1 , r1, x2, y2 ,r2 ,..., xn, yn , rn. Построить на экране окружности с центром в точке (xi, yi) и радиусами ri, для которых выполнено условие ri > 5.
250 Даны натуральные числа n, x1 , y1 , r1, x2, y2 ,r2 ,..., xn, yn , rn. Построить на экране окружности с центром в точке (xi, yi) и радиусами ri, если ri > 5, и радиусами 2ri в противном случае.
(*) - В ряде задач этого и следующих параграфов требуется вычислить сумму или произведение тех членов последовательности, которые обладают заданным свойством. Можно условится, что при отсутствии таких членов искомая сумма равна нулю, а произведение - единице. Можно усложнить условие задач, приняв соглашение, что в подобных случаях далжно выдаваться сообщение об отсутствии соответствующих членов.
(**) - В качестве ответов к этой и ряду других задач, в которых требуется определить истинность какого - либо утверждения, должны быть получены соответствующие текстовые сообщения.
-
a) являющихся нечетными числами;
б) кратных 3 и не кратных 5;
в) являющихся квадратами четных чисел;
г) удовлетворяющих условию
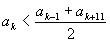
д) удовлетворяющих условию 2k < ak < k!;
е) имеющих четные порядковые номера и являющихся нечтными числами.
179 Данные натуральные числа n,q1,...,qn. найти те члены qi последовательности q1,...,qn, которые
-
a) являются удвоенными нечетными числами;
б) при делении на 7 дают остаток 1, 2 или 5;
в) обладают тем свойством, что корни уравнения x2 + 3qi-5 действительны и положительны.
180 Дано натуральное число n. Получить сумму тех чисел вида i3 -3in2 + n (i = 1,2,...,n), которые явлются утроенными нечетными.(*)
181 Даны целые числа a1,...a50. Получить сумму тех чисел данной последовательности, которые
-
а)кратные 5;
б)нечетные и отрицательные;
в)удовлетворяют условию |ai| < i2
182 Даны натуральное число n, целые часла a1,...,an. Найти количество и сумму тех членов данной последовательности, которые делятся на 5 и не делятся на 7.
183 Даны натуральные числа n, p, целые числа a1,...,an. Получить произведение членов последовательности a1,...,an, кратных p.
184 Даны целые числа p, q, a1,...,a67 (p > q ≥ 0). В последовательности a1, ..., a67 заменить нулями члены, модуль которых при делении на p дает в остатке q.
185 Даны натуральное число n, действительные числа a1,...,an. Получить удвоенную сумму всех положительных членов последовательности a 1,...,an.
186 Даны натуральное число n, действительные числа a1,...,an. Вычислить обратную величину произведения тех членов ai последовательности a1,..., an, для которых выполнено i+1<ai<i!.
187 Даны натуральное число n,действительные числа a1,..., an. В последовательности a1,...,an все отрицательные члены увеличить на 0.5, а все неотрицательные заменить на 0.1.
188 Даны натуральное число n, действительные числа x1,..., xn. В последовательности x1,..., xn все члены, меньшие двух, заменить нулями. Кроме того, получить сумму членов, принадлежащих отрезку [3,7], а также число таких членов.
189 Даны натурльное число n, действительные числа a1 ,...,an. В последовательности a1 ,...,an все неотрицательные члены, не принадлежащие отрезку [1,2], заменить на единицу. Кроме того, получить число отрицательных членов и число членов, принадлежащих отрезку [1,2].
190 Даны натеральное число n, целые числа a1,...,an. Получить сумму положительных и число отрицательных членов последовательности a1,...,an.
191 Даны натуральное число n, целые числа a1,...,an. Заменить все большие семи члены последовательности a1,...,an числом 7. Вычислить количество таких членов.
192 Даны целые числа a1,...,a45. Получить число отрицательных членов последовательности a1,...,a35 и число нулевых членов всей последовательности a1,...,a45.
193 Пусть xо = a; xk = qxk-1+b (k = 1,2,...). Даны неотрицательное целое n, действительные a, b, c, d, q (c<d). Пренадлежит ли xn интервалу (c, d)?
194 Даны натуральнее число n, целые числа а, х1 , ..., хn. Если в последовательности х1 , ..., хn есть хотя бы один член, равный а, то получить сумму всех членов, следующих за первым таким членом; в противном случае ответом должно быть число -10.
195 Даны натуральное число n, действительные числа а, b, c1 , ..., cn. Верно ли(**), что при 1 ≤ k ≤ n-1 всякий раз, когда ck < a, выполнено ck+l > b?
196 Даны целые числа a1,...,a50. Получить последовательность b1,...,b50, которая отличается от исходной тем, что все нечётные члены удвоны.
197 Вычислить
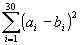, где
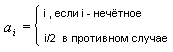
198 Даны натуральные числа n, b0,...,bn. Вычислить f (b0) + f (b1) +...+ f (bn), где
199 Даны натуральное число n, действительные числа r, a1,...,an (n ≥ 2). Сколько среди точек (a1, an), (a2, an-1),..., (an, a1) таких, которые принадлежат кругу радиуса r с центром в начале координат?
200 Даны целые числа a, n, x1,...,xn(n > 0). Определить, каким по счету идёт в последовательности x1,...,xn член, равный a. Если такого члена нет, то ответом должно быть число 0.
201 Даны натуральное число n, действительные числа a1,...,an. Получить:
-
а) max (a1,...,an);
б) min (a1,...,an);
в) max (a2,a4,...);
г) min (a1,a3,...);
д) min (a2,a4,...) + max (a1,a3,...);
е) max (|a1|,...,|an|);
ж) max (-a1,a2,-a3,...,(-1)nan);
з) (min (a1,...,an))2- min(a12,..., an2).
202 Даны натуральное число n, действительные числа a1,...,an.
-
а) Верно ли, что отрицательных членов в последовательности a1,...,an больше, чем
положительных?
б) Верно ли, что наибольший член последовательности a1,...,an по модулю больше единицы?
203 У прилавка в магазине выстроилась очередь из n покупателей. Время обслуживания продавцом i-го покупателя равно ti (i = 1,...,n). Пусть даны натуральное n и действительные t1,...,tn. Получить c1,...,cn, где ci - время прибывания i-го покупателя в очереди (i = 1,...,n). Указать номер покупателя, для обслуживания которого продавцу потребовалось самое малое время.
204 В некоторых видах спортивных состязаний выступление каждого спортсмена независимо оценивается несколькими судьями, затем из всей совокупности оценок удаляются наибдолее высокая и наиболее низкая, а для оставшихся оценок вычисляется среднее арифметическое, которое и идет в зачет спортсмену. Если наиболее высокую оценку выставило несколько судей, то из совокупности оценок удаляется только одна такая оценка; аналогично поступают с наиболее низкими оценками.
- Даны натуральное число n, действительные положительные числа a1,...,an (n ≥ 3).
Считая, что числа a1,...,an - это оценки, выставленные судьями одному из участников
соревнований, определить оценку, которая пойдет в зачет этому спортсмену.
205 Даны натуральное число n, действительные числа a1,...,an. Получить max (|a1|,...,|an|) и
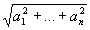.206 Дано натуральное число n. Найти наибольшее среди чисел kesin2(k+1) (k = 1,...,n), а также сумму всех этих чисел.
207 Дано натуральное число n. Выбросить из записи числа n цифры 0 и 5, оставив прежним порядок остальных цифр. Например, из числа 59015509 должно получиться 919.
208 Даны натеральное число n, целые числа a1,...,an.Найти:
-
а) наименьшее их четных чисел, входящих в последовательность a1-1, a1,
a2,..., an;
б) наибольшее из нечетных и количество четных чисел, входящих в последовательность a1,..., an, an+1.
209 Даны натуральное число n, действительное число x. Среди чисел ecos(x2k)sin(x3k) (k = 1,...,n) найти ближайшее к какому - нибудь целому.
210 Даны натуральное число n, действительные числа a1,...,an. Получить все натуральные j (2 ≤ j ≤ n-1), для которых aj-1 < aj > aj+1.
211 Пусть x1 = 0.3; x2 = -0.3; xi = i + sin(xi-2), i=3,4,... Среди x1,...,x100 найти ближайшее к какому - нибудь целому.
212 Пусть x1 = y1 = 1;
;
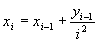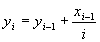, i = 2, 3.... Получить x8, y18.213 Пусть
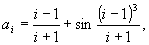, i=1,2,...Дано натуральное n. Среди a1,...,an найти все положительные числа, среди положительных a1,...,an выбрать наименьшее число.
214 Пусть ao = cos21; a1 = - sin21; ak = 2ak-1 - ak-2, k = 2,3,...
- Найти сумму квадратов тех чисел
a1,...,a100 которые не превосходят двух.
215 Даны натуральное число n, действительные числа a1,...,an. В последовательности a1,...,an, определить число соседств:
-
а) двух положительных чисел;
б) двух чисел разного знака;
в) двух чисел одного знака, причём модуль первого числа должен быть больше модуля второго числа.
216 Даны целые числа c1,...,c95. Имеются ли в последовательности c1,...,c95:
-
а) два идущих подряд нулевых члена;
б) три идущих подряд нулевых члена?
217 Даны натуральное число n, действительные числа x1,...,x3n. Последовательность чисел x1,...,x3n определяет на плоскости n квадратов со сторонами, параллельными координатным осям: так, x1, x2 - координаты центра первого квадрата, x3 - длина его стороны; аналогично, числа x4, x5, x6 определяют второй квадрат, x7, x8, x9 - третий и т.д. Имеются ли точки, принадлежащие всем квадратам? Если да, то указать координаты одной из них.
218 Даны натуральное число n, действительные числа x1,...,x3n. Вычислить сумму из xn+1,...,x3n, которые превосходят по величине все числа x1,...,xn.
219 Даны действительные числа a,b (a < b), натуральное число n, функция y = f(x) , определенная на отрезке [a,b]. Для значений аргумента xi=a+ih (i=0,1,...,n), h = (b-a)/n вычислить значения функции yi = f(xi)(i=0,1,..,n).
-
Вывести xi и yi (i=0,1,...,n) в виде таблицы из двух колонок. В i-ю строку таблицы заносятся соответствующие значения xi и yi.
Рассмотреть следующие функции:
-
а) y = sinx + cos2x, a = - π, b = π, n = 50;
б)
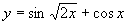, a = 0, b = 2π, n = 50;в)
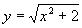, a = -3, b = 5, n = 40;г) y = x|x + 1|, a = - 1, b = 2, n = 30;
д) y = xe-x, a = - 1, b = 3, n = 40.
220 Рассматривается последовательность a1,...,a1000. Требуется определить, сколько членов последовательности с номерами 1,2,4,8,16,... имеют значение, меньшее, чем 0.25. При этом считать, что
-
а) ak=sin2(3k+5)-cos(k2-15), k = 1,2,...,1000;
б) a1,...,a1000 - заданные действительные числа;
в) a1=0.01; ak=sin(k+ak-1), k = 2,...,1000.
221 Даны натуральное число n, действительные числа x1,...,xn. Получить (1+r)/(1+s), где r - сумма всех трех членов последовательности x1,...,xn, которые не превосходят 1, а s - сумма членов, больших 1.
222 Даны натуральное число n, действительные числа y1,..., yn. Найти:
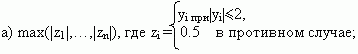
б)
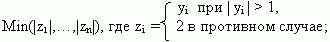
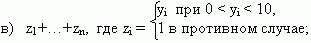
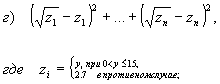
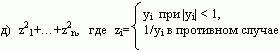
223 Даны целые числа a1,a2,... Известно, что a1 > 0 и что среди a2,a3,... есть хотябы одно отрицательное число. Пусть a1,..., an - члены данной последовательности, предшествующие первому отрицательному члену (n заранее неизвестно). Получить:
-
а) max (a12, ..., an2);
б) max (a13, ..., an3);
в) min (a1, 2a2, ..., nan);
г) min (a1 + a2, a2 + a3, ..., an-1 + an);
д) max (a1,...,a1a2, ..., ,a1a2...an);
e) количество четных среди a1,...,an;
ж) количество удвоенных нечетных среди a1,...,an;
з) количество полных квадратов среди a1,...,an;
и) количество квадратов нечетных чисел среди a1,...,an;
224 Дано натуральное число n. Получить все его натуральные делители.
225 Дано натуральное число n. Получить все такие натуральные q, что n делится на q2 и не делится на q3.
226 Даны натуральные числа m, n. Получить все их натуральные общие кратные, меньшие mn.
227 Даны целые числа m, n (m ≠ 0, n ≠ 0). Получить все их общие делители (положительные и отрицательные).
228 Даны натуральное число n, действительные числа a1,..., an. Выяснить, является ли последовательность a1,...,an упорядоченной по убыванию.
229 Даны действительные числа x, y (x >0, y >1). Получить целое число k (пложительное, отрицательное или равное нулю), удовлетворяющее условию yk-1 ≤ x < yk.
230 Даны натуральное число n, действительные числа a1,..., an. Найти длину наименьшего отрезка числовой оси, содержащего числа a1,..., an.
231 Даны действительные числа x, y1,...,y12. Выяснить, во-первых, верно ли, что y1 ≤ x ≤ y12 и, во-вторых, верно ли, что t1 ≤ x ≤ t2, где t1 - наименьшее, а t2 - наибольшее среди y1,...,y12. (Какие комбинации ответов на первый и второй вопросы возможны?)
232 Даны натуральное число n, действительные числа a, x1,..., xn (x1 ≤ x2 ≤ ... ≤ xn). Получить последовательность y1,...,yn+1, членами которой являются члены последовательности x1,...,xn и значение a, такую, что y1 ≤ y2 ≤ ... ≤ yn+1.
233 Даны натуральное число n, целые числа a1,..., an. Оставить без изменения последовательность a1,...,an, если её члены упорядочены по неубыванию или по невозрастанию. В противном случае получить подпоследовательность a1,...,am(m < n), где m таково, что либо a1 ≤ a2 ≤ ... ≤ am и am > am+1, либо a1 ≥ a2 ≥ ... ≥ am и am < am+1.
234 Даны натуральное число n, действительные числа x1,..., xn. Получить в порядке следования все xk, удовлетворяющие неравенствам xk > x1, xk > x2,...,xk > xk-1.
235 Даны натуральные числа m и n. Получить:
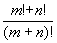
236 Даны натуральное число n, действительное число x. Получить:
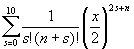
237 Даны натуральное число n, действительное число r.
- Вычислить
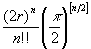(см. задачу
113.)238 Дано натуральное число n. Вычислить произведение первых n сомножителей
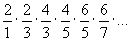
239 Дано натуральное число n. Вычислить
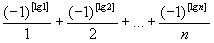.240 Для любого целого k обозначим количество цифр в его десятичной записи через Ц(k).
-
а) Дано натуральное число n. Вычислить
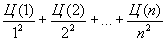.б) Даны натуральное число n, действительное число x. Вычислить
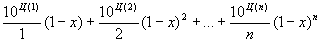.241 Дано натуральное число n, действительное число x. Вычислить
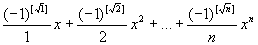.242 Дано натуральное число n. Вычислить
.
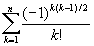243 Дано натуральное число n. Можно ли представить его в виде суммы двух квадратов натуральных чисел? Если можно, то
-
а) указать пару x, y таких натуральных чисел, что n=x2+y2;
б) указать все пары x, y, таких натуральных чисел, что n=x2+y2, x ≥ y.
244 Даны натуральное число n, целые числа a1,...,an.
-
а) Выяснить какое число встречается в последовательности a1,...,an раньше -
положительное или отрицательное. Если все члены последовательности равны нулю, то сообщить об оэтом.
б) Найти номер первого четного члена последовательность a1,...,an; если четных членов нет, то ответом должно быть число 0.
в) Найти номер последнего нечетного члена последовательности a1,...,an; если нечетных членов нет, то ответом должно быть число n+1.
245 Даны натуральное число n, целые числа a1,..., a30, b1,...,b40, c1,...,cn. Верно ли, что отрицательный член в последовательности c1,...,cn встречается раньше, чем в последовательностях a1,...,a30 и b1,..., b40? Предпологается, что каждая из последовательностей содержит хотя бы один отрицательный член.
246 Даны натуральное число n, действительные числа a1,..., an. Выяснить, образуют ли возрастающую последовательность числа:
-
а) a1,...,an, 2a1, 3a2,...,
(n+1)an;
б)a1 ,..., an , an+1, an-1+2 ,..., a1+n;
в)a1 ,..., an , n(an-1+1) , (n-1) (an-2+2) ,..., 2(a1+n-1).
247 Даны натуральные числа n, x0 , y0 , r, x1, y1 ,..., xn, yn. Построить на экране точки с координатами xi, yi:
-
а) принадлежащие кругу с центром в точке (x0 , y0) и радиусом r;
б) не принадлежащие кругу с центром в точке (x0 , y0) и радиусом r.
248 Даны натуральные числа n, x1, y1, x2, y2 ,..., xn, yn. Построить на экране точки с координатами xi, yi:
-
а) расположенные в верхней половине экрана;
б) расположенные в нижней половине экрана.
249 Даны натуральные числа n, x1 , y1 , r1, x2, y2 ,r2 ,..., xn, yn , rn. Построить на экране окружности с центром в точке (xi, yi) и радиусами ri, для которых выполнено условие ri > 5.
250 Даны натуральные числа n, x1 , y1 , r1, x2, y2 ,r2 ,..., xn, yn , rn. Построить на экране окружности с центром в точке (xi, yi) и радиусами ri, если ri > 5, и радиусами 2ri в противном случае.
(*) - В ряде задач этого и следующих параграфов требуется вычислить сумму или произведение тех членов последовательности, которые обладают заданным свойством. Можно условится, что при отсутствии таких членов искомая сумма равна нулю, а произведение - единице. Можно усложнить условие задач, приняв соглашение, что в подобных случаях далжно выдаваться сообщение об отсутствии соответствующих членов.
(**) - В качестве ответов к этой и ряду других задач, в которых требуется определить истинность какого - либо утверждения, должны быть получены соответствующие текстовые сообщения.
Предыдущая глава