271 Даны действительные числа a1,...,a15. Получить
272 Даны действительные числа a1901, a1902 ,..., a1950 - количество осадков (в миллиметрах), выпавших в Москве в течение первых 50 лет нашего столетия. Надо вычислить среднее количество осадков и отклонений от среднего для каждого года.
273 Система из 25 материальных точек в пространстве задена с помощью последовательности действительных чисел x1, y1, z1, p1, x2, y2, z2, p2,...,x25, y25, z25, p25, где xi, yi, zi - координаты i-ой точки, pi- её вес (i=1,2,...,25). Получить координаты центра тяжести системы, а так же расстояния от центра тяжести до всех точек системы.
274 Даны действительные числа a1,...,a20. Получить числа b1,...,b20, где bi - среднее арифметическое всех членов последовательности a1,...,a20, кроме (i=1,2,...,20).
275 Даны действительные числа x1,...,x10, y1,...,y10. Получить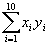 . Как упростить решение,
если исходные данные будут иметь следующий порядок: x1y1,...,
x10y10?
. Как упростить решение,
если исходные данные будут иметь следующий порядок: x1y1,...,
x10y10?
276 Построить последовательность целых чисел a1,...,a30, где a1=1; a2=1; ai=a[i/2]+ai-2 (i=3,...,30).
277 Даны действительные числа a1,...,an. Получить an, an-1,...,a1.
278 Даны натуральные числа n1,...,n20, действительные числа x1,...,x20. Вычислить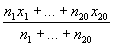 .
.
279 Даны действительные числа a1,...,an, b1,...,bn. Вычислить (a1+bn)(a2+bn-1)... (an+b1).
280 Пусть xi, yi (i=1,2,...) определены, как в задаче 167. Получить x1,...,x25, y1,...,y25.
281 Даны действительные числа a1,...,a28, b1,..., b28. Члены последовательности c1,...,c29 связаны с членами данных последовательностей соотношениями c29=0,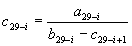 (i=1,...,29).
Получить c1,...,c29
(i=1,...,29).
Получить c1,...,c29
282 Даны действительные числа a1, a2,...,a2n. Получить:
283 Даны действительные числа a1,...,a17. Получить:
284 Даны действительные числа a1,...,a20. Получить:
285 Даны действительные числа a1,...,an. Если в результате замены отрицательных членов последовательности a1,...,an их квадратами члены будут образовывать неубывающую последовательность, то получить сумму членов исходной последовательности; в противном случае получить их произведение.
286 Даны действительные числа a1,...,a99. Получить новую последовательность, выбросив из исходной все члены со значением max(a1,..., a99).
287 Даны целые числа a1,...,an. Все члены последовательности с четными номерами, предшествующие первому по порядку члену со значением max(a1,...,an), домножить на max(a1,...,an).
288 Даны целые числа a1,...,an, каждое из которых отлично от нуля. Если в последовательности отрицательные и положительные члены чередуются (+, -, +, -,... или -, +, -, +,... ), то ответом должна служить сама исходная последовательность. Иначе получить все отрицательные члены последовательности, сохранив порядок их следования.
289 Даны натуральное число m, действительные числа a1,..., a30 (числа a1,...,a30 попарно различны, m≤30). В последовательности a1,...,a30 поменять местами наибольший член и член с номером m.
290 Даны действительные числа x1,...,x101, y1,..., y101. Получить действительные x'1,...,x'101, y'1,...,y' 101, преобразовав для получения x'i, y'i члены xi, yi по правилу: если они оба отрицательны, то каждый из них увеличить на 0.5; если отрицательно только одно число, то отрицательное число заменить его квадратом; если оба числа неотрицательны, то каждое из них заменить на среднее арифметическое исходных значений.
291 Даны действительные числа a1,...,a30. Получить:
292 Даны действительные числа a1,...,a20. Преобразовать эту последовательность по правилу: большее из ai и a10+i (i=1,...,10) принять в качестве нового значения ai, а меньшее - в качестве нового значения a10+i.
293 Даны целые числа a1,...,an. Если в данной последовательности ни одно четное число не расположено после нечетного, то получить все отрицательные члены последовательности, иначе - все положительные. Порядок следования чисел в обоих случаях заменяется на обратный.
294 Даны действительные числа r1,...,r17, среди которых заведомо есть как отрицательные, так и неотрицательные. Получить x1y1+...+xs ys, где x1,...,xp - отрицательные члены последовательности r1,...,r17 взятые в порядке их следования, y1,...,yq - неотрицательные члены, взятые в обратном порядке,
s = min(p,q).
295 Даны целые числа a1,...,a20. Наименьший член последовательности a1,...,a20 заменить целой частью среднего арифметического всех членов, остальные члены оставить без изменения. Если в последовательности несколько членов со значением min(a1,...,a20), то заменить последний по порядку.
296 Даны действительные числа a1,...,a20(все числа попарно различны). Поменять в этой последовательности местами:
297 Даны целые числа a1,...,a100. Получить новую последовательность из 100 целых чисел, заменяя ai нулями, если |ai| не равно max(a1,...,a100)и заменяя ai единицей в противном случае (i=1,...,100 ).
298 Даны целые числа a1,...,a25, b1,..., b25. Преобразовать последовательность b1,...,b25 по правилу: если ai ≤ 0, увеличить bi в 10 раз, иначе bi, заменить нулем (i =1, ..., 25).
299 Даны действительные числа a1,...,a26. Требуется домножить все члены последовательности a1,...,a26 на квадрат ее наименьшего члена, если a1 ≥ 0, и на квадрат ее наибольшего члена, если a1 < 0.
300 Даны натуральное число n, действительные числа a1,..., an . Получить b1,...,b10 где bi равно сумме тех членов последовательности a1,...,an, которые принадлежат полуинтервалу (i-1, i] (i=1, . . ., 10). Если полуинтервал не содержит членов последовательности, то соответствующее bi положить равным нулю.
301 Даны действительные числа x1, y1, x2, y2,...,x20, y20 , r1 , r2,..., r11 (0 < r1 < r2< ...< r11). Пары (x1, y1), (x2, y2),...,(x20, y20) рассматриваются как координаты точек на плоскости. Числа r1,...,r11 рассматриваются как радиусы одиннадцати полукругов в полуплоскости у > 0 с центром в начале координат. Найти количество точек, попадающих внутрь каждого полукруга (границы - полуокружности не принадлежат полукругам).
302 Дано натуральное число n. Сколько различных цифр встречается в его десятичной записи?
303 Даны действительные числа x1,...,x200 , принадлежащие полуинтервалу (0,1]. Полуинтервал разбивается на 100 равных частей. Вычислить p1,..., p100, где pk=mk/2000, а mk - количество заданных чисел, принадлежащих полуинтервалу (0.01 (k-1), 0.01k] (k=1,...,100).
304 Даны действительные числа a1,...,a16. Переставить члены последовательности a1,...,a16 так, чтобы сначала расположились все ее неотрицательные члены, а потом - все отрицательные. Иначе говоря, после перестановки должно найтись такое k, что 1 ≤ k ≤ 16, и если i ≤ k, то аi ≥ 0; если i > k, то аi < 0 (i= 1, . . ., 16). Порядок как среди неотрицательных членов, так и среди отрицательных должен быть сохранен прежним.
305 Даны действительные числа a1,...,a30. Оставить без изменения последовательность a1,...,a30, если она упорядочена по неубыванию или по невозрастанию; в противном случае удалить из последовательности те члены, порядковые номера которых кратны четырем, сохранив прежним порядок оставленных членов.
306 Даны натуральные числа x1, y1, x2, y2,...,xn, yn. Числа xi, yi являются координатами точек. Построить на экране точки, заданные последовательностью x1, y1, x2, y2,...,xn, yn, а затем удалить их. Процесс построения должен начинаться точкой с номером 1 и заканчиваться точкой с номером n; процесс удаления точек должен происходить в обратном порядке - начиная точкой с номером n и заканчивая точкой с номером 1.
307 Даны натуральные числа x1, y1, x2, y2,...,xn, yn. Числа xi, yi являются координатами точек. Построить на экране точки, заданные последовательностью x1, y1, x2, y2,...,xn, yn. Точки должны строиться поочерёдно: построение каждой последующей точки должно сопровождаться удалением предыдущей. Процесс построения следует выполнить дважды: первый раз начиная точкой с номером 1 и кончая точкой с номером n, второй раз - в обратном порядке - начиная точкой с номером n и заканчивая точкой с номером 1.
308 В условие предыдущей задачи вносится изменение: поочередное построение точек следует выполнять так, чтобы после появления на экране первых трех точек построение каждой новой точки сопровождалось удалением точки, которая была построена раньше трех других видимых точек.
309 Даны натуральные числа x1, y1, r1, x2, y2, r2,...,xn, yn, rn. Числа xi, yi являются центрами кругов радиуса ri. Построить на экране круги, заданные последовательностью x1, y1, r1, x2, y2, r2,...,xn, yn, rn, а затем закрасить их (одним и тем же цветом или разными цветами). Процесс построения должен начинаться кругом с номером 1 и заканчиваться кругом с номером n; процесс закраски должен происходить в обратном порядке - начиная кругом с номером n и заканчивая кругом с номером 1.
310 Даны натуральные числа x, y, r1, r2,...,rn. Числа ri являются сторонами квадратов с центрами в точке (x, y). Построить на экране квадраты, заданные последовательностью r1, r2,...,rn, а затем удалить их. Процесс построения должен начинаться квадратом с номером 1 и заканчиваться квадратом с номером n; процесс удаления должен происходить в обратном порядке - начиная квадратом с номером n и заканчивая квадратом с номером 1.
311 Даны натуральные числа x1, y1, r1, x2, y2, r2,...,xn, yn, rn. Построить на экране окружности с центрами в точках (xi, yi)и радиусами ri, если среди r1, r2,...,rn, найдется число, меньше 5, и квадраты с центрами в точках (xi, yi) и сторонами ri в противном случае.
312 Даны символы s1,...,sn. Оставить последовательность s1,...,sn без изменения, если в нее не входит символ *, иначе каждый символ /, предшествующий первому вхождению символа *:
313 Даны символы s1,...,sn. Если последовательность s1,...,sn является палиндромом, т. е. s1=sn, s2=sn-1,..., то оставить ее без изменения, иначе получить последовательность s1, s2,...,sn-1, sn, sn-1,...,s2, s1.
314 Даны символы s1,...,s66. Если последовательность s1,...,s66 такова, что s1=s34, s2=s35, ...,s33=s66 то оставить ее без изменения, иначе получить последовательность s1, s2,..., s66, s1, s2,..., s66.
315 Даны символы s1,...,s80. Определить количество неверных равенств среди:
316 Даны натуральное число n, символы s1,...,sn. Будем рассматривать слова, образованные символами, входящими в последовательность s1,..., sn. (см. задачу 269), считая при этом, что количество символов в каждом слове не превосходит 15.
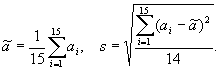
272 Даны действительные числа a1901, a1902 ,..., a1950 - количество осадков (в миллиметрах), выпавших в Москве в течение первых 50 лет нашего столетия. Надо вычислить среднее количество осадков и отклонений от среднего для каждого года.
273 Система из 25 материальных точек в пространстве задена с помощью последовательности действительных чисел x1, y1, z1, p1, x2, y2, z2, p2,...,x25, y25, z25, p25, где xi, yi, zi - координаты i-ой точки, pi- её вес (i=1,2,...,25). Получить координаты центра тяжести системы, а так же расстояния от центра тяжести до всех точек системы.
274 Даны действительные числа a1,...,a20. Получить числа b1,...,b20, где bi - среднее арифметическое всех членов последовательности a1,...,a20, кроме (i=1,2,...,20).
275 Даны действительные числа x1,...,x10, y1,...,y10. Получить
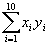 . Как упростить решение,
если исходные данные будут иметь следующий порядок: x1y1,...,
x10y10?
. Как упростить решение,
если исходные данные будут иметь следующий порядок: x1y1,...,
x10y10?276 Построить последовательность целых чисел a1,...,a30, где a1=1; a2=1; ai=a[i/2]+ai-2 (i=3,...,30).
277 Даны действительные числа a1,...,an. Получить an, an-1,...,a1.
278 Даны натуральные числа n1,...,n20, действительные числа x1,...,x20. Вычислить
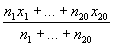 .
.279 Даны действительные числа a1,...,an, b1,...,bn. Вычислить (a1+bn)(a2+bn-1)... (an+b1).
280 Пусть xi, yi (i=1,2,...) определены, как в задаче 167. Получить x1,...,x25, y1,...,y25.
281 Даны действительные числа a1,...,a28, b1,..., b28. Члены последовательности c1,...,c29 связаны с членами данных последовательностей соотношениями c29=0,
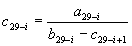 (i=1,...,29).
Получить c1,...,c29
(i=1,...,29).
Получить c1,...,c29282 Даны действительные числа a1, a2,...,a2n. Получить:
-
а) a1, an+1, a2, an+2,..., an, a2n;
б) a1, a2n, a2, a2n-1, a3,...,an, an+1;
в) a1+a2n, a2+a2n-1,...,an+an+1.
283 Даны действительные числа a1,...,a17. Получить:
-
а) a17, a1, a2,...,a16;
б) a11, a12,..., a17, a1, a2,..., a10;
в) a11, a12,...,a17, a10, a9,..., a1
284 Даны действительные числа a1,...,a20. Получить:
-
а) a20, a11, a19, a10,...,a10, a1;
б)a1, a3,...,a19, a2, a4,...,a20;
в) a1, a11, a3, a13,...,a9, a19;
г) a12, a2, a14, a4,...,a20, a10;
д) a1, a11, a12, a2, a3, a13, a14, a4,..., a9, a19, a20, a10;
285 Даны действительные числа a1,...,an. Если в результате замены отрицательных членов последовательности a1,...,an их квадратами члены будут образовывать неубывающую последовательность, то получить сумму членов исходной последовательности; в противном случае получить их произведение.
286 Даны действительные числа a1,...,a99. Получить новую последовательность, выбросив из исходной все члены со значением max(a1,..., a99).
287 Даны целые числа a1,...,an. Все члены последовательности с четными номерами, предшествующие первому по порядку члену со значением max(a1,...,an), домножить на max(a1,...,an).
288 Даны целые числа a1,...,an, каждое из которых отлично от нуля. Если в последовательности отрицательные и положительные члены чередуются (+, -, +, -,... или -, +, -, +,... ), то ответом должна служить сама исходная последовательность. Иначе получить все отрицательные члены последовательности, сохранив порядок их следования.
289 Даны натуральное число m, действительные числа a1,..., a30 (числа a1,...,a30 попарно различны, m≤30). В последовательности a1,...,a30 поменять местами наибольший член и член с номером m.
290 Даны действительные числа x1,...,x101, y1,..., y101. Получить действительные x'1,...,x'101, y'1,...,y' 101, преобразовав для получения x'i, y'i члены xi, yi по правилу: если они оба отрицательны, то каждый из них увеличить на 0.5; если отрицательно только одно число, то отрицательное число заменить его квадратом; если оба числа неотрицательны, то каждое из них заменить на среднее арифметическое исходных значений.
291 Даны действительные числа a1,...,a30. Получить:
-
а) max (a1+a30, a2+a29,...,a15+a16);
б) min (a1a16, a2a17,...,a15a30).
292 Даны действительные числа a1,...,a20. Преобразовать эту последовательность по правилу: большее из ai и a10+i (i=1,...,10) принять в качестве нового значения ai, а меньшее - в качестве нового значения a10+i.
293 Даны целые числа a1,...,an. Если в данной последовательности ни одно четное число не расположено после нечетного, то получить все отрицательные члены последовательности, иначе - все положительные. Порядок следования чисел в обоих случаях заменяется на обратный.
294 Даны действительные числа r1,...,r17, среди которых заведомо есть как отрицательные, так и неотрицательные. Получить x1y1+...+xs ys, где x1,...,xp - отрицательные члены последовательности r1,...,r17 взятые в порядке их следования, y1,...,yq - неотрицательные члены, взятые в обратном порядке,
s = min(p,q).
295 Даны целые числа a1,...,a20. Наименьший член последовательности a1,...,a20 заменить целой частью среднего арифметического всех членов, остальные члены оставить без изменения. Если в последовательности несколько членов со значением min(a1,...,a20), то заменить последний по порядку.
296 Даны действительные числа a1,...,a20(все числа попарно различны). Поменять в этой последовательности местами:
-
а) наибольший и наименьший члены;
б) наибольший и последний члены.
297 Даны целые числа a1,...,a100. Получить новую последовательность из 100 целых чисел, заменяя ai нулями, если |ai| не равно max(a1,...,a100)и заменяя ai единицей в противном случае (i=1,...,100 ).
298 Даны целые числа a1,...,a25, b1,..., b25. Преобразовать последовательность b1,...,b25 по правилу: если ai ≤ 0, увеличить bi в 10 раз, иначе bi, заменить нулем (i =1, ..., 25).
299 Даны действительные числа a1,...,a26. Требуется домножить все члены последовательности a1,...,a26 на квадрат ее наименьшего члена, если a1 ≥ 0, и на квадрат ее наибольшего члена, если a1 < 0.
300 Даны натуральное число n, действительные числа a1,..., an . Получить b1,...,b10 где bi равно сумме тех членов последовательности a1,...,an, которые принадлежат полуинтервалу (i-1, i] (i=1, . . ., 10). Если полуинтервал не содержит членов последовательности, то соответствующее bi положить равным нулю.
301 Даны действительные числа x1, y1, x2, y2,...,x20, y20 , r1 , r2,..., r11 (0 < r1 < r2< ...< r11). Пары (x1, y1), (x2, y2),...,(x20, y20) рассматриваются как координаты точек на плоскости. Числа r1,...,r11 рассматриваются как радиусы одиннадцати полукругов в полуплоскости у > 0 с центром в начале координат. Найти количество точек, попадающих внутрь каждого полукруга (границы - полуокружности не принадлежат полукругам).
302 Дано натуральное число n. Сколько различных цифр встречается в его десятичной записи?
303 Даны действительные числа x1,...,x200 , принадлежащие полуинтервалу (0,1]. Полуинтервал разбивается на 100 равных частей. Вычислить p1,..., p100, где pk=mk/2000, а mk - количество заданных чисел, принадлежащих полуинтервалу (0.01 (k-1), 0.01k] (k=1,...,100).
304 Даны действительные числа a1,...,a16. Переставить члены последовательности a1,...,a16 так, чтобы сначала расположились все ее неотрицательные члены, а потом - все отрицательные. Иначе говоря, после перестановки должно найтись такое k, что 1 ≤ k ≤ 16, и если i ≤ k, то аi ≥ 0; если i > k, то аi < 0 (i= 1, . . ., 16). Порядок как среди неотрицательных членов, так и среди отрицательных должен быть сохранен прежним.
305 Даны действительные числа a1,...,a30. Оставить без изменения последовательность a1,...,a30, если она упорядочена по неубыванию или по невозрастанию; в противном случае удалить из последовательности те члены, порядковые номера которых кратны четырем, сохранив прежним порядок оставленных членов.
306 Даны натуральные числа x1, y1, x2, y2,...,xn, yn. Числа xi, yi являются координатами точек. Построить на экране точки, заданные последовательностью x1, y1, x2, y2,...,xn, yn, а затем удалить их. Процесс построения должен начинаться точкой с номером 1 и заканчиваться точкой с номером n; процесс удаления точек должен происходить в обратном порядке - начиная точкой с номером n и заканчивая точкой с номером 1.
307 Даны натуральные числа x1, y1, x2, y2,...,xn, yn. Числа xi, yi являются координатами точек. Построить на экране точки, заданные последовательностью x1, y1, x2, y2,...,xn, yn. Точки должны строиться поочерёдно: построение каждой последующей точки должно сопровождаться удалением предыдущей. Процесс построения следует выполнить дважды: первый раз начиная точкой с номером 1 и кончая точкой с номером n, второй раз - в обратном порядке - начиная точкой с номером n и заканчивая точкой с номером 1.
308 В условие предыдущей задачи вносится изменение: поочередное построение точек следует выполнять так, чтобы после появления на экране первых трех точек построение каждой новой точки сопровождалось удалением точки, которая была построена раньше трех других видимых точек.
309 Даны натуральные числа x1, y1, r1, x2, y2, r2,...,xn, yn, rn. Числа xi, yi являются центрами кругов радиуса ri. Построить на экране круги, заданные последовательностью x1, y1, r1, x2, y2, r2,...,xn, yn, rn, а затем закрасить их (одним и тем же цветом или разными цветами). Процесс построения должен начинаться кругом с номером 1 и заканчиваться кругом с номером n; процесс закраски должен происходить в обратном порядке - начиная кругом с номером n и заканчивая кругом с номером 1.
310 Даны натуральные числа x, y, r1, r2,...,rn. Числа ri являются сторонами квадратов с центрами в точке (x, y). Построить на экране квадраты, заданные последовательностью r1, r2,...,rn, а затем удалить их. Процесс построения должен начинаться квадратом с номером 1 и заканчиваться квадратом с номером n; процесс удаления должен происходить в обратном порядке - начиная квадратом с номером n и заканчивая квадратом с номером 1.
311 Даны натуральные числа x1, y1, r1, x2, y2, r2,...,xn, yn, rn. Построить на экране окружности с центрами в точках (xi, yi)и радиусами ri, если среди r1, r2,...,rn, найдется число, меньше 5, и квадраты с центрами в точках (xi, yi) и сторонами ri в противном случае.
312 Даны символы s1,...,sn. Оставить последовательность s1,...,sn без изменения, если в нее не входит символ *, иначе каждый символ /, предшествующий первому вхождению символа *:
-
а) заменить на запятую;
б) удалить из последовательности.
313 Даны символы s1,...,sn. Если последовательность s1,...,sn является палиндромом, т. е. s1=sn, s2=sn-1,..., то оставить ее без изменения, иначе получить последовательность s1, s2,...,sn-1, sn, sn-1,...,s2, s1.
314 Даны символы s1,...,s66. Если последовательность s1,...,s66 такова, что s1=s34, s2=s35, ...,s33=s66 то оставить ее без изменения, иначе получить последовательность s1, s2,..., s66, s1, s2,..., s66.
315 Даны символы s1,...,s80. Определить количество неверных равенств среди:
-
а) s1=s41, s2=s42,..., s40=s80;
б) s1=s80, s2=s79,...,s40=s41
316 Даны натуральное число n, символы s1,...,sn. Будем рассматривать слова, образованные символами, входящими в последовательность s1,..., sn. (см. задачу 269), считая при этом, что количество символов в каждом слове не превосходит 15.
-
а) Найти какое - нибудь слово, оканчивающееся буквой д (если таких слов нет, то сообщить об этом).
б) Найти какое - нибудь слово, начинающееся буквой а и оканчивающееся буквой я (если таких слов нет, то сообщить об этом).
в) Удалить из s1,...,sn все слова с нечетными порядковыми номерами и перевернуть все слова с четными номерами. Например, если n = 21 и данная последовательность символов представляет собой последовательность
-
во_что_бы_то_ни_стало
то должна получиться последовательность
-
отч_от_олатс
г) Удалить из s1,...,sn все слова, в которых встречается не более двух различных букв.
д) Удалить из s1,...,sn все слова, оканчивающиеся группой букв кая или кое.
 Предыдущая глава
Предыдущая глава