317 Даны действительные числа a1,...,a10. Вычислить
a1+a22+...+a1010.
318 Дано натуральное число n. Получить f0f1...fn, где
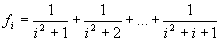 .
.
319 Дано действительные числа a1,...,a24. Получить последовательность b1, ..., b10, где b1 = a1+a2 +...+ a24,
b2 = a12 + a23 + ... + a242, b10 = a110 + a210 + ... + a2410
320 Вычилить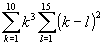 .
.
321 Даны натуральные числа m,n, действительные числа a1,a2,..., amn. Вычислить
a1a2...am +am+1am+2... a2m+a(n-1)m+1a(n-1)m+2...anm.
322 Найти натуральное число от 1 до 10000 с максимальной суммой делителей.
323 Дано натуральное число n. Получить все натуральные числа, меньшие n и взаимно простые с ним.
324 Даны целые числа p и q. Получить все делители числа q, взаимно простые с p.
325 Дано натуральное число n. Получить все простые делители этого числа.
326 Найти наименьшее натуральное число n, представимое двумя различными способами в виде суммы кубов двух натуральных чисел X3 + Y3 (X ≥ Y) .
327 Даны натуральные числа a, b (a ≤ b). Получить все простые числа р, удовлетворяющие неравенствам a ≤ p ≤ b.
328 Найти 100 первых простых чисел.
329 Даны натуральные числа n, m. Получить все меньшие n натуральные числа, квадрат суммы цифр которых равен m.
330 Натуральное число называется совершенным, если оно равно сумме всех своих делителей, за исключением себя самого. Число 6-совершенное, так как 6 = 1 + 2 + 3. Число 8-не совершенное, так как 8 ≠ 1 + 2 + 4. Дано натуральное число n. Получить все совершенные числа, меньшие n.
331 Дано натуральные число n. Можно ли представить его в виде суммы трех квадратов натуральных чисел? Если можно, то
332 Известно, что любое натуральное число можно представить в виде суммы не более чем четырех квадратов натуральных чисел или, что то же самое, в виде суммы четырех квадратов неотрицательных целых чисел (теорема Лагранжа). Дано натуральное n; указать такие неотрицательные целые х, у, z, t, что n = x2 + y2 + z2 + t2.
333 Даны натуральные числа m, n1, ..., nm (m ≥ 2). Вычислить НОД(n1, ..., nm), воспользовавшись для этого соотношением НОД(n1, ..., nk) = НОД(НОД(n1, ..., nk-1)nk) (k = 3, ..., n) и алгоритмом Евклида (см. задачу 89).
334 Вычислить:
335 Дано натуральное число n. Вычислить:
336 Даны натуральное число n, действительное число х. Вычислить:
337 Даны действительные числа а, b (а < b), натуральное число n, функция y = f(x), определенная на отрезке [a, b]. Вывести на печатающее устройство график функции. Для построения графика вычислить значения функции yi = f(xi), где xi = a + ih, i = 0, 1, ..., n, h = (b - a)/n.
338 Даны натуральное число n, целые числа a1,..., a25, b1,..., bn. Среди a1,..., a25 нет повторяющихся чисел, нет их и среди b1,..., bn.
339 Даны целые числаa a1,..., an (в этой последовательности могут быть повторяющиеся члены).
340 Даны целые числа m, a1,..., a20. Найти три натуральных числа i, j, k, каждое из которых не превосходит двадцати, такие, что ai+ aj+ ak = m. Если таких чисел нет, то сообщить об этом.
341 Даны пять различных целых чисел. Найти среди них два числа, модуль разности которых имеет:
342 Даны действительные числа х, y1,..., y25. В последовательности y1,..., y25 найти два члена, среднее арифметическое которых ближе всего к х.
343 Даны действительные числа x1,..., x17. Найти сумму значений |xi - xj| (1 ≤ i < j ≤ 17).
344 Даны действительные числа a1,..., a10, натуральное число m. Последовательность b1,b2,... образована по закону -
345 Пусть t0 = 1,tk=t0tk-1+t1t k-2+...+tk-2t1+tk-1t0, k = 1,2,...
346 Даны натуральное число k, действительное число а (а > 0). Последовательность x0,x1...образована по закону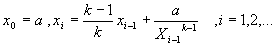
347 Даны целые числа a1,..., a30. Пусть М-наибольшее, а m-наименьшее из a1,..., a30. Получить в порядке возрастания все целые из интервала (m, М), которые не входят в последовательность a1,..., a30.
348 Даны целые числа a1,..., an,b1,..., bn. Верно ли, что эти две последовательности отличаются не более чем порядком следования членов?
349 Даны целые числа a1,..., an. Для каждого из чисел, входящих в последовательность a1,..., an, выяснить, сколько раз оно входит в эту последовательность. Результат представить в виде ряда строк, первая из которых есть a1-k, где k-число вхождений a1 в последовательность a1,..., an . Вторая строка будет иметь вид ai-m, где ai-первый, по порядку член последовательности, отличный от a1,а m-число вхождений этого члена в последовательность.
350 Даны натуральные числа k, n, действительные числа a1,..., akn. Получить:
351 Даны натуральные числа a1,...an. Известно, что a1,...an-перестановка чисел 1, ..., n, т. е. в последо-вательности a1,... an встречаются все числа 1, ..., n, Будем говорить, что натуральное m переводится данной перестановкой в натуральное k(m ≤ n, k ≤ n) , если am= k. Например, число 1 переводится в a1,a1 переводится в aa1 и т. д. Рассмотрим образованную этим способом последовательность 1, a1, aa1 ,...
352 Пусть цвета экрана имеют номера 0, 1, ..., k. Высветить все точки экрана (или точки некоторой прямо-угольной области) различными цветами, используя для точки с координатами i, j цвет с номером, равным остатку от деления |m| на k+ 1, где m-может быть взято, например, равным:
353 Даны натуральные числа x1,y1, ..., x10, y10. Получить на экране точки (x1,y1),(x2,y2),..., (x10,y10)которые входят в эту последовательность ровно один раз.
354 Даны натуральные числа x1,y1, ..., xn,yn. Построить на экране точки с координатами xi,yi, (i=1, ...,n) и соединить отрезками прямых:
355 Даны натуральные числа x1,y1, ...,xn,yn. Построить на экране точки с координатами xi,yi (i = 1,...,n) и соединить пары наибoлее удаленных друг от друга.
356 Даны натуральные числа x1, y1, c1,..., xn, yn, cn. Каждые три числа xi,yi,ci, задают координаты точки и её цвет (i=1, ...,n). Из точек одного цвета получить на экране:
357 Даны натуральные числа x1,y1,r1, ..., xn,yn,rn которые задают последовательность окружностей так, что xi, yi-координаты центра, а ri-радиус i-й окружности (i=1, ...,n). Получить на экране окружности, которые имеют общие точки с некоторыми другими окружностями последовательности.
358 Получить окружности, указанные в предыдущей задаче, и дополнительно целиком закрасить каким-нибудь одним цветом часть экрана, покрываемую кругами, ограниченными этими окружностями (рис, 17).
Рис.17
359 Даны натуральное число n, символы s1,..., s10, t1,..., tn. Получить все не превосходящие n-9 натуральные i, для которых s1 = ti, s2 = ti+1 , ..., s10 = ti+9.
360 Даны натуральное число n, символы s1, ... sn. Найти все палиндромические начальные отрезки последовательности s1,..., sn, т. е. такие отрезки s1,..., sk (k ≤ n), что s1 = sk, s2= sk-1...
361 Даны натуральное число n, символы s1, ..., sn. Указать все натуральные i для которых 2i ≤ n и S1=Si+1, S2=Si+2,..., Si=S2i
362 Даны символы s1 ,...,sn. Найти такое наибольшее натуральное i, что 2i < n, s1=si+1, s2=si+2,...,si=s2i и s1,s2,...,si-палиндром, т. е. s1=si, s2=si-1
363 Даны натуральное число n, символы s1 ,...,sn. Преобразовать последовательность s1 ,...,sn, добавив к ней наименьшее число символов sn+1 ,...,sm, так, чтобы последовательность s1 ,...,sm, стала палиндромом: s1 =si, s2 =sm-1
364 Даны символы s1,..., s50. Выяснить, верно ли, что хотя бы один символ входит в s1 ,...,s50 более одного раза и при этом так, что между любыми двумя его вхождениями встречается буква а или b.
365 Даны натуральное число n, символы s1 ,...,sn. Будем рассматривать слова, образованные символами, входящими в последовательность s1 ,..., sn (см. задачу 269), считая при этом, что количество символов в каждом слове не превосходит 15.
366 Даны символы a1,..., a10, натуральное число n, символы s1 ,...,sn. Как и в предыдущей задаче, будем рассматривать слова, входящие в последовательность s1 ,...,sn, по-прежнему считая, что количество символов в каждом слове не превосходит 15. Будем также считать, что среди символов a1 ,...,a10 нет пробелов, и поэтому последовательность a1 ,...,a10 может рассматриваться как одно слово. В словах могут встретиться ошибки:
318 Дано натуральное число n. Получить f0f1...fn, где
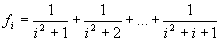 .
.319 Дано действительные числа a1,...,a24. Получить последовательность b1, ..., b10, где b1 = a1+a2 +...+ a24,
b2 = a12 + a23 + ... + a242, b10 = a110 + a210 + ... + a2410
320 Вычилить
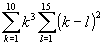 .
.321 Даны натуральные числа m,n, действительные числа a1,a2,..., amn. Вычислить
a1a2...am +am+1am+2... a2m+a(n-1)m+1a(n-1)m+2...anm.
322 Найти натуральное число от 1 до 10000 с максимальной суммой делителей.
323 Дано натуральное число n. Получить все натуральные числа, меньшие n и взаимно простые с ним.
324 Даны целые числа p и q. Получить все делители числа q, взаимно простые с p.
325 Дано натуральное число n. Получить все простые делители этого числа.
326 Найти наименьшее натуральное число n, представимое двумя различными способами в виде суммы кубов двух натуральных чисел X3 + Y3 (X ≥ Y) .
327 Даны натуральные числа a, b (a ≤ b). Получить все простые числа р, удовлетворяющие неравенствам a ≤ p ≤ b.
328 Найти 100 первых простых чисел.
329 Даны натуральные числа n, m. Получить все меньшие n натуральные числа, квадрат суммы цифр которых равен m.
330 Натуральное число называется совершенным, если оно равно сумме всех своих делителей, за исключением себя самого. Число 6-совершенное, так как 6 = 1 + 2 + 3. Число 8-не совершенное, так как 8 ≠ 1 + 2 + 4. Дано натуральное число n. Получить все совершенные числа, меньшие n.
331 Дано натуральные число n. Можно ли представить его в виде суммы трех квадратов натуральных чисел? Если можно, то
-
а) указать тройку х, у, z таких натуральных чисел, что n = x2 + y2 + z2;
б) указать все тройки х, у, z таких натуральных чисел, что n = x2 + y2 + z2.
332 Известно, что любое натуральное число можно представить в виде суммы не более чем четырех квадратов натуральных чисел или, что то же самое, в виде суммы четырех квадратов неотрицательных целых чисел (теорема Лагранжа). Дано натуральное n; указать такие неотрицательные целые х, у, z, t, что n = x2 + y2 + z2 + t2.
333 Даны натуральные числа m, n1, ..., nm (m ≥ 2). Вычислить НОД(n1, ..., nm), воспользовавшись для этого соотношением НОД(n1, ..., nk) = НОД(НОД(n1, ..., nk-1)nk) (k = 3, ..., n) и алгоритмом Евклида (см. задачу 89).
334 Вычислить:
-
a)
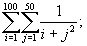 .
.б)
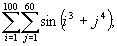 .
.в)
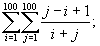 .
.г)
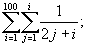 .
.335 Дано натуральное число n. Вычислить:
-
a)
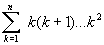 ;
;б)
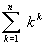 ;
;в)
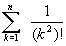 ;
;г)
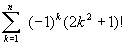 ;
;
336 Даны натуральное число n, действительное число х. Вычислить:
-
а)
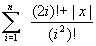 ;
;б)
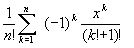 ;
;в)
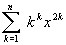 ;
;г)
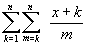 ;
;
337 Даны действительные числа а, b (а < b), натуральное число n, функция y = f(x), определенная на отрезке [a, b]. Вывести на печатающее устройство график функции. Для построения графика вычислить значения функции yi = f(xi), где xi = a + ih, i = 0, 1, ..., n, h = (b - a)/n.
- Ось Ox расположить вертикально, ось Оу-горизонтально. Шаг по оси Ox-это переход на
новую строку, шаг по оси Оу-позиция следующего символа в текущей строке. Точки графика изображать символом *.
- Рассмотреть следующие функции:
-
а) у = | sin x | + cos |x|, а = 0, b = π, n = 40;
б) y = 2sinx + 3cosx,a = -π, b = π, n = 50;
в)
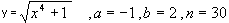 ;
;г) y = 1/(x2 - x + 1), a = -1, b = 3, n = 40;
д) y = (x - 3)/(x2 + 2), a = -1, b = 4, n = 50;
е) y = x2e-|x|, a = -1, b = 3, n = 40;
ж) y = e-xsin2x, a = -π/2, b = 2π, n = 50;
з)
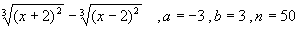 ;
;
338 Даны натуральное число n, целые числа a1,..., a25, b1,..., bn. Среди a1,..., a25 нет повторяющихся чисел, нет их и среди b1,..., bn.
-
а) Построить пересечение последовательностей a1,..., a25 и b1,...,
bn(т. е. получить в каком-нибудь порядке все числа, принадлежащие последовательности
a1,..., a25 и последовательности b1,..., bnодновременно).
б) Построить объединение данных последовательностей.
в) Получить все члены последовательности b1,..., bn, которые не входят в последовательность a1,..., a25.
г) Верно ли, что все члены последовательности a1,..., a25 входят в последовательность b1,..., bn?
д) Верно ли, что все члены последовательности b1,..., bn входят в последовательность a1,..., a25.
е) Верно ли, что все члены последовательности a1,..., a25 входят в последовательность b1,..., bnи при этом а1 встречается в последовательности b1,..., bn не позднее, чем a2,a2-не позднее, чем a3, и т. д.?
339 Даны целые числаa a1,..., an (в этой последовательности могут быть повторяющиеся члены).
-
а) Получить все числа, которые входят в последовательность по одному разу.
б) Получить числа, взятые по одному из каждой группы равных членов.
в) Найти число различных членов последовательности.
г) Выяснить, сколько чисел входит в последовательность по одному разу.
д) Выяснить, сколько чисел входит в последовательность более чем по одному разу.
е) Выяснить, имеется ли в последовательности хотя бы одна пара совпадающих чисел.
340 Даны целые числа m, a1,..., a20. Найти три натуральных числа i, j, k, каждое из которых не превосходит двадцати, такие, что ai+ aj+ ak = m. Если таких чисел нет, то сообщить об этом.
341 Даны пять различных целых чисел. Найти среди них два числа, модуль разности которых имеет:
-
а) наибольшее значение;
б) наименьшее значение.
342 Даны действительные числа х, y1,..., y25. В последовательности y1,..., y25 найти два члена, среднее арифметическое которых ближе всего к х.
343 Даны действительные числа x1,..., x17. Найти сумму значений |xi - xj| (1 ≤ i < j ≤ 17).
344 Даны действительные числа a1,..., a10, натуральное число m. Последовательность b1,b2,... образована по закону -
-
b1=a1,...,b10=a10,
bk=bk-1+bk-2+...+bk-10, k = 11,12,...
- Получить bm.
345 Пусть t0 = 1,tk=t0tk-1+t1t k-2+...+tk-2t1+tk-1t0, k = 1,2,...
- Получить t10.
346 Даны натуральное число k, действительное число а (а > 0). Последовательность x0,x1...образована по закону
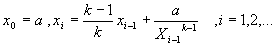
- Hайти первое значение xn, для которого |xnk-a|<10-4
(последовательность x0,x1... сходится к
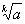 ).
).347 Даны целые числа a1,..., a30. Пусть М-наибольшее, а m-наименьшее из a1,..., a30. Получить в порядке возрастания все целые из интервала (m, М), которые не входят в последовательность a1,..., a30.
348 Даны целые числа a1,..., an,b1,..., bn. Верно ли, что эти две последовательности отличаются не более чем порядком следования членов?
349 Даны целые числа a1,..., an. Для каждого из чисел, входящих в последовательность a1,..., an, выяснить, сколько раз оно входит в эту последовательность. Результат представить в виде ряда строк, первая из которых есть a1-k, где k-число вхождений a1 в последовательность a1,..., an . Вторая строка будет иметь вид ai-m, где ai-первый, по порядку член последовательности, отличный от a1,а m-число вхождений этого члена в последовательность.
350 Даны натуральные числа k, n, действительные числа a1,..., akn. Получить:
-
а) последовательность a1+...+ak,ak+1+...+a2k,...,
ak(n-1)+1+...+akn;
б) последовательность max(a1,...,ak), max(ak+1,...,a2k),..., max (ak(n-1)+1,...,akn);
в) min (a1, ..., ak) + min (ak+1, ..., a2k) + ... + min(ak(n-1)+1,..., akn);
г) max(a1+...+ak,ak+1+...+a2k,ak(n-1)+1 +...+ akn);
д) min (max (а1, ..., аk), max (аk+1, ...,a2k ), ..., max(ak(n-1)+1, ...,akn)).
351 Даны натуральные числа a1,...an. Известно, что a1,...an-перестановка чисел 1, ..., n, т. е. в последо-вательности a1,... an встречаются все числа 1, ..., n, Будем говорить, что натуральное m переводится данной перестановкой в натуральное k(m ≤ n, k ≤ n) , если am= k. Например, число 1 переводится в a1,a1 переводится в aa1 и т. д. Рассмотрим образованную этим способом последовательность 1, a1, aa1 ,...
-
а) Доказать, что первый член этой последовательности, для которого имеется равный среди предыдущих, есть 1.
Получить по порядку все члены последовательности 1, a1, aa1, ..., предшествующие
повторению числа 1.
б) Кроме той последовательности, которую требуется получить в а), получить аналогичные последовательности, начинающиеся с чисел, больших 1. При этом последовательности должны быть попарно различны, и каждая из них должна начинаться с наименьшего члена. Например, если n = 6, a1=3, a2=2, a3=5, a4=6, a5=1, a6=4, то должны быть получены последовательности.
-
1, 3, 5
2,
4, 6
352 Пусть цвета экрана имеют номера 0, 1, ..., k. Высветить все точки экрана (или точки некоторой прямо-угольной области) различными цветами, используя для точки с координатами i, j цвет с номером, равным остатку от деления |m| на k+ 1, где m-может быть взято, например, равным:
-
а) i+j;
б) (i-10)2+25j2;
в) (i-50)2-j;
г) 25(i+5)+(i-5)j2;
д) (i-50)2-(j-50)3;
е) (i2+j2)2-2(i2-j2);
353 Даны натуральные числа x1,y1, ..., x10, y10. Получить на экране точки (x1,y1),(x2,y2),..., (x10,y10)которые входят в эту последовательность ровно один раз.
354 Даны натуральные числа x1,y1, ..., xn,yn. Построить на экране точки с координатами xi,yi, (i=1, ...,n) и соединить отрезками прямых:
-
а) каждую из n точек со всеми остальными n-1 точками;
б) точки с номерами одной четности;
в) точки с номерами разной четности.
355 Даны натуральные числа x1,y1, ...,xn,yn. Построить на экране точки с координатами xi,yi (i = 1,...,n) и соединить пары наибoлее удаленных друг от друга.
356 Даны натуральные числа x1, y1, c1,..., xn, yn, cn. Каждые три числа xi,yi,ci, задают координаты точки и её цвет (i=1, ...,n). Из точек одного цвета получить на экране:
-
а) первую;
б) последнюю.
357 Даны натуральные числа x1,y1,r1, ..., xn,yn,rn которые задают последовательность окружностей так, что xi, yi-координаты центра, а ri-радиус i-й окружности (i=1, ...,n). Получить на экране окружности, которые имеют общие точки с некоторыми другими окружностями последовательности.
358 Получить окружности, указанные в предыдущей задаче, и дополнительно целиком закрасить каким-нибудь одним цветом часть экрана, покрываемую кругами, ограниченными этими окружностями (рис, 17).

Рис.17
359 Даны натуральное число n, символы s1,..., s10, t1,..., tn. Получить все не превосходящие n-9 натуральные i, для которых s1 = ti, s2 = ti+1 , ..., s10 = ti+9.
360 Даны натуральное число n, символы s1, ... sn. Найти все палиндромические начальные отрезки последовательности s1,..., sn, т. е. такие отрезки s1,..., sk (k ≤ n), что s1 = sk, s2= sk-1...
361 Даны натуральное число n, символы s1, ..., sn. Указать все натуральные i для которых 2i ≤ n и S1=Si+1, S2=Si+2,..., Si=S2i
362 Даны символы s1 ,...,sn. Найти такое наибольшее натуральное i, что 2i < n, s1=si+1, s2=si+2,...,si=s2i и s1,s2,...,si-палиндром, т. е. s1=si, s2=si-1
363 Даны натуральное число n, символы s1 ,...,sn. Преобразовать последовательность s1 ,...,sn, добавив к ней наименьшее число символов sn+1 ,...,sm, так, чтобы последовательность s1 ,...,sm, стала палиндромом: s1 =si, s2 =sm-1
364 Даны символы s1,..., s50. Выяснить, верно ли, что хотя бы один символ входит в s1 ,...,s50 более одного раза и при этом так, что между любыми двумя его вхождениями встречается буква а или b.
365 Даны натуральное число n, символы s1 ,...,sn. Будем рассматривать слова, образованные символами, входящими в последовательность s1 ,..., sn (см. задачу 269), считая при этом, что количество символов в каждом слове не превосходит 15.
-
а) Найти наибольшую длину слов палиндромов. (Если палиндромов нет, то ответом должно быть число 0).
б) Выяснить, верно ли, что каждое слово, не являющееся палиндромом, имеет четную длину.
в) Выяснить, имеются ли два слова, каждое из которых получается переворачиванием другого.
г) Удалить из s1 ,...,sn все слова, встречающиеся более двух раз.
366 Даны символы a1,..., a10, натуральное число n, символы s1 ,...,sn. Как и в предыдущей задаче, будем рассматривать слова, входящие в последовательность s1 ,...,sn, по-прежнему считая, что количество символов в каждом слове не превосходит 15. Будем также считать, что среди символов a1 ,...,a10 нет пробелов, и поэтому последовательность a1 ,...,a10 может рассматриваться как одно слово. В словах могут встретиться ошибки:
-
1) переставлены две соседние буквы;
2) заменена одна буква;
3) пропущена одна буква.
- Требуется найти в s1 ,...,sn все слова, из которых могло бы получиться
a1 ,...,a10в результате одной ошибки.
 Предыдущая глава
Предыдущая глава