628 Рассмотрим массив целых или действительных чисел a1, ...,
an. Пусть требуется переставить элементы этого массива так, чтобы после перестановки они были
упорядочены по неубыванию: a1 ≤ a2 ≤ ... ≤ an. Эта задача
называется задачей сортировки или упорядочения массива (эту же задачу можно рассматривать применительно к
упорядочению по невозрастанию: a1 ≥ a2 ≥ ... ≥ an; если
числа попарно различны, то можно говорить об убывании и о возрастании). Для решения этой задачи можно
воспользоваться, например, следующими алгоритмами:
629 Исследовать число сравнений и число перемещений (т.е. перестановок с одного места на другое) элементов a1, ..., an в процессе применения описанных в предыдущей задаче алгоритмов. Показать, что число перемещений для алгоритма сортировки выбором ограничено некоторой линейной функцией от n. В это же время и число сравнений для алгоритма сортировки выбором, и обе указанные характеристики для алгоритмов сортировки обменами и сортировки простыми вставками в некоторых случаях (например, когда исходный массив таков, что a1 > a2 >... >an) являются квадратичными функциями от n.
630 Из утверждения предыдущей задачи следует, что алгоритм сортировки выбором выгодно отличается от алгоритмов сортировки обменами и сортировки простыми вставками в тех случаях, когда перемещение элемента оказывается существенно более сложным делом, чем сравнение элементов. Использовать это при выполнении следующих заданий.
631 Пусть дан упорядоченный по неубыванию массив целых или действительных чисел a1 ≤ a2 ≤ ... ≤ an и пусть дано некоторое число b (соответственно целое или действительное), для которого нужно найти такое место среди чисел a1, ..., an, чтобы после вставки числа b на это место упорядоченность не нарушилась. Если вследствие равенства между собой некоторых элементов массива число b можно вставлять на разные места, то требуется определить ближайшее к началу массива место. Эта задача называется задачей поиска места элемента. Для b имеется n + 1 возможность: b ≤ a1, a1 < b ≤ a2, ..., an-1 < b ≤ an, an < b, и решением задачи поиска места элемента b будет соответственно одно из чисел 1, ..., n + 1. Для решения задачи полезен алгоритм, который называется алгоритмом деления пополам: взять первоначально 1 и n + 1 в качестве границ поиска места элемента; далее, до тех пор, пока границы не совпадут, шаг за шагом сдвигать эти границы следующим образом: сравнить b с as, где s-целая часть среднего арифметического границ; если as < b, то заменить прежнюю нижнюю границу на s + 1, а верхнюю оставить без изменения, иначе оставить без изменения нижнюю границу, а верхнюю заменить на s; когда границы совпадут, став равным некоторому числу t, выполнение вышеописанного алгоритма закончится с результатом t. (Число сравнений, требуемых этим алгоритмом, не превосходит [log2(n + 1)] + 1).
632 Даны действительные числа a1, ..., an, p, натуральное число k (a1 ≤ a2 ≤ ... ≤ an, k ≤ n). Удалить из a1, ..., an элемент с номером k (т.е. ak) и вставить элемент, равный p, так, чтобы не нарушилась упорядоченность.
633 Алгоритм упорядочения простыми вставками (см. алгоритм в) в задаче 628) можно изменить следующим образом: место, на которое надо вставить ai в уже упорядоченную совокупность ai, ..., ai-1, определяется алгоритмом деления пополам (см. задачу 631). Получится новый алгоритм сортировки, который называется алгоритмом сортировки бинарными вставками (слова"бинарная вставка" следует понимать как "вставка делением пополам"). Этот алгоритм требует всего около n log2n сравнением элементов. Написать программу, реализующую этот алгоритм.
634 Даны целые числа a1, ..., an. Получить в порядке возрастания все различные числа, входящие в a1, ..., an. Здесь удобно воспользоваться алгоритмом сортировки вставками (если n велико, то лучше применить бинарные вставки; если n сравнительно мало, скажем, n<50, то можно обойтись и простыми вставками). В процессе сортировки следует отбрасывать элементы, уже встречавшиеся раньше. Если в результате поиска места ai в упорядоченной совокупности a1, ..., ak (k < i) обнаружится, что среди a1, ..., ak есть элемент, равный ai, то следует перейти к рассмотрению ai + 1 без изменения a1, ..., ak.
635 Даны действительные числа c1, ..., cp, d1, ..., dg(c1 ≤ c2 ≤ ... ≤ cp, d1 ≤ d2 ≤ ... ≤ dg). Внести единую упорядоченность в c1, ..., cp, d1, ..., dg, получив f1, f2, ..., fp + g такие, что f1 ≤ f2 ≤ ... ≤ fp + g. Число сравнений не должно превосходить p + g.
636 Алгоритм фон Неймана упорядочения массива a1, ..., an по неубыванию (алгоритм сортировки слияниями) основан на многократных слияниях уже упорядоченных групп элементов массива (см. предыдущую задачу). В начале весь массив рассматривается как совокупность упорядоченных групп по одному элементу в каждом. Слиянием соседних групп получаем упорядоченные группы, каждая из которых содержит два элемента (кроме, может быть, последней группы, которой не нашлось парной). Далее, упорядоченные группы укрупняются тем же способом и т. д. Здесь приходится оперировать не только с массивом a1, ..., an, но и с вспомогательным массивом b1, ..., bn (первоначальные значения его элементов не играют роли). Рис. 34 демонстрирует два последовательных этапа укрупнения: массивы a1, ..., an и b1, ..., bn представлены в виде отрезков, которые разбиты на части, изображающие упорядоченные группы. Число упорядоченных групп убывает, следовательно, настанет такой момент, когда в массиве a1, ..., an или b1, ..., bn будет содержаться только одна упорядоченная группа. А это означает, что массив упорядочен. Для слияния двух упорядоченных групп, содержащих соответственно p и g элементов, достаточно произвести не более p + g сравнений. Следовательно, для одного этапа укрупнения достаточно произвести не более n сравнений. Столько же требуется на одном этапе и перемещений. Можно показать, что алгоритм фон Неймана требует в целом приблизительно n log2n сравнений и столько же перемещений. Из рассмотренных до сих пор алгоритмов только алгоритм сортировки бинарными вставками требовал столь небольшого числа сравнений. Онако алгоритм фон Неймана выгодно отличается от последнего алгоритма тем, что требует меньше перемещений элементов a1, ..., an (хотя и требует дополнительного массива b1, ..., bn). Написать программу, реализующую алгоритм фон Неймана.
638 На преобразовании массива, описанном в предыдущей задаче, основывается следующий рекурсивный алгоритм сортировки (так называемая быстрая сортировка). Если массив содержит не более одного элемента, то он упорядочен. Иначе применяем к нему преобразование, описанное в предыдущей задаче, и определяем результат применения алгоритма быстрой сортировки к a1, ..., an следующим образом: вначале идет первая группа элементов, упорядоченная с помощью алгоритма быстрой сортировки, затем без изменения тот элемент, который разделял первую и вторую группы элементов, затем вторая группа элементов, упорядоченная с помощью алгоритма быстрой сортировки. Этот алгоритм не использует дополнительного массива и требует в среднем приблизительно nlog2n сравнений и столько же перемещений элементов. Правда, это лишь среднее число: в худшем случае число соавнений может достигать n(n-1)/2; кроме того, алгоритм быстрой сортировки содержит рекурсии.
Написать программу, реализующую алгоритм быстрой сортировки.
639 На преобразовании массива, описанном в задаче 637, основывается также следующий алгоритм поиска значения k-го по величине элемента массива a1, ..., an (т. е. того элемента, который бы занял место с номером k после упорядочения массива). Пусть в результате преобразования, описанного в задаче 637, первый элемент занял p-е место; если k = p, то поиск закончен; если k < p, то надо перейти к поиску k - го по величине элемента в начальной группе элементов, содержащей p-1 элемент (задача упростилась, так как p - 1 < n); если же k > p, то надо перейти к поиску (k - p) - го по величине элемента во второй группе элементов (задача упростилась, так как n - p < n). Этот алгоритм не содержит рекурсий. Не пользуясь рекурсиями, написать программу, реализующую этот алгоритм.
640 Нетрудно заметить, что алгоритм, описанный в предыдущей задаче, фактически позволяет найти не только k-й по величине элемент, но и дополнительно 1 - й, 2 - й, ..., (k - 1) - й элементы, хотя и в неупорядоченном виде. Основываясь на этом, выполнить следующие задания :
641 Алгоритм сортировки обменами (см. алгоритм б) в задаче 628) также имеет свои достоинства. Рассмотрим следующий пример. Пусть слова, которые можно выделить в массиве символов a1, ..., an (см. задачу 269), требуется представить в лексикографическом порядке. Так как разные слова могут иметь разную длину, то без больших затруднений можно менять местами только слова, стоящие рядом. Но алгоритм сортировки обменами и предписывает только такие обмены. Эта задача не является, конечно, задачей сортировки массива, но тем не менее алгоритм сортировки обменами оказывается здесь полезным. Написать программу, предполагая, что длина слова не превосходит пятнадцати.
642 Алгоритм б), сформулированный в задаче 628 , - это, строго говоря, лишь один из алгоритмов сортировки обменами. Он иногда называется алгоритмом пузырька. Есть и другие алгоритмы, которые естественно отнести к алгоритмам сортировки обменами. Приведем пример такого алгоритма. Последовательным просмотром чисел a1, ..., an найти наименьшее i такое, что ai > ai + 1. Поменять ai и ai + 1 местами и возобновить просмотр с начала массива. Когда не удастся найти такое i, массив будет упорядочен нужным образом. Написать программу, реализующую этот алгоритм.
643 Рассмотреть все алгоритмы сортировки, сформулированные в этом параграфе, и указать достоинства и недостатки кажлого из них. Необходимо помнить, что в случае небольших массивов те алгоритмы, которые сформулировнны в задаче 628, дают вполне удовлетворительное решение задачи. При больших n требуется тщательно изучить все особенности конкретной ситуации и, исходя из этого, подобрать алгоритм. Задачи сортировки массивов возникают не только в связи с числовыми массивами. Тип элементами может быть довольно сложным, и надо учитывать, во что обходится сравнение и перемещение элементов в том или ином случае.
644 Даны пять попарно различных чисел a, b, c, d, e. Упорядочить их по возрастанию, используя для этого не более семи сравнений.
645 Даны действительные числа a1, ..., an. Получить попарно различные целые i1, ..., in такие, что 1 ≤ ik ≤ n, k = 1, ..., n и ai1 ≥ ai2 ≥ ... ≥ ain.
646 Даны натуральное число n, целые числа a1, ..., an. Найти наибольшее значение, встречающееся в последовательности a1, ..., an, после выбрасывания из нее
647 Даны натуральное число n, действительные числа a1, ..., an. Требуется найти max (a1, ..., an) и min (a1, ..., an). Рассмотрим два алгоритма решения этой задачи. Первый алгоритм. Шаг за шагом получить пары max (a1, ..., ai), min (a1, ..., ai) (i = 1, ..., n). При этом, чтобы получить max (a1, ..., ai + 1), min (a1, ..., ai + 1), сравнивается ai + 1 с max (a1, ..., ai), а затем, если ai + 1 < max (a1, ..., ai), дополнительно сравнивается ai + 1 с min (a1, ..., ai). Второй алгоритм. Пусть n - четное число, т.е. n = 2k. Тогда шаг за шагом получать max (a1, ..., a2l), min (a1, ..., a2l) (l = 1, ..., k). При этом, чтобы получить max (a1, ..., a2l + 2), min (a1, ..., a2l + 2), вначале сравниваются между собой a2l + 1, a2l + 2 и max (a2l + 1, a2l + 2) сравнивается с max (a1, ..., a2l), а min(a2l + 1, a2l + 2) - с min (a1, ..., a2l). Если n -нечетное число, то потребуется еще дополнительный шаг: сравнение последнего элемента и an с max (a1, ..., an-1) и, возможно, с min (a1, ..., an-1).
648 Даны натуральные числа a1, ..., an. Пусть a1, ..., an - перестановка чисел 1, ..., n. Получить натуральные r1, ..., rn такие, что rai = i для i = 1, ..., n.
649 Решить задачи 646, 647, предполагая, что числа a1, ..., an являются компонентами данного файла. При этом значение n неизвестно заранее.
650 Число компонент файла f, компонентами которого являются целые числа, кратно десяти. Переписать компоненты файла f в файл q, изменяя порядок чисел в каждой десятке так, чтобы
651 Рассматриваются слова (см. задачу 269), содержащиеся в символьных файлах f1 и f2. Известно, что число символов в словах не превосходит шестнадцати. Известно также, что слова в файле f2 идут в лексикографическом порядке и их число равно пятидесяти. Выяснить, сколько раз каждое из слов файла f2 встречается в файле f1. Для решения задачи переписать слова, содержащиеся в файле f2, в массив и последовательно применять метод деления пополам (см. задачу 631).
652 Пусть файлы c и d с компонентами, являющимися действительными или целыми числами, упорядочены по невозрастанию компонент. Требуется собрать компоненты файлов c и d в упорядоченном виде в файле f (ср. c задачей 635). Количество сравнений не должно превосходить p + g, где p и g - число компонент в файлах c и d.
653 Пусть a и b - файлы, k - натуральное число. Будем говорить, что файлы a и b согласованно k - упорядочены, если
655 Пусть файлы а и b, компоненты которых являются целыми числами, упорядочены по неубыванию. Получить в файле с все числа файлов а и b без повторений. Файл с должен быть упорядочен по возрастанию.
656 Дан файл f, компоненты которого являются целыми числами. Получить в файле g все нечётные числа, входящие в файл f. Числа в файле g должны следовать:
657 Дан символьный файл f, компоненты которого - малые латинские буквы и пробелы. Слова (см. задачу 269) файла f имеют не более шестнадцати букв. Записать эти слова в файл g в лексикографическом порядке.
* В задачах 628 - 648 этого параграфа существенно, что данные рассматриваются в программе как массив; в задачах 649 - 657 рассматриваются файлы, и это усложняет некоторые алгоритмы.
а) Найти элемент массива, имеющий наименьшее значение, переставить его с первым элементом, затем проделать то же самое, начав со второго элемента и т.д.(Сортировка выбором.)
б) Последовательным просмотром чисел a1, ..., an найти наименьшее i такое, что ai > ai + 1. Поменять ai и ai + 1 местами, возобновить просмотр с элемента ai + 1 и т.д. Тем самым наибольшее число передвинется на последнее место. Следующие просмотры начинать опять сначала, уменьшая на единицу количество просматриваемых элементов. Массив будет упорядочен после просмотра, в котором участвовали только первый и второй элеменеы. (Сортировка обменами.)
в) Просматривать последовательно a2, ..., an и каждый новый элемент ai вставлять на подходящее место в уже упорядоченную совокупность ai, ..., ai-1. Это место определяется последовательным сравнением ai с упорядоченными элементами a1, ai-1. (Сортировка простыми вставками).
- Написать программы, реализующие алгоритмы а), б), в).
629 Исследовать число сравнений и число перемещений (т.е. перестановок с одного места на другое) элементов a1, ..., an в процессе применения описанных в предыдущей задаче алгоритмов. Показать, что число перемещений для алгоритма сортировки выбором ограничено некоторой линейной функцией от n. В это же время и число сравнений для алгоритма сортировки выбором, и обе указанные характеристики для алгоритмов сортировки обменами и сортировки простыми вставками в некоторых случаях (например, когда исходный массив таков, что a1 > a2 >... >an) являются квадратичными функциями от n.
630 Из утверждения предыдущей задачи следует, что алгоритм сортировки выбором выгодно отличается от алгоритмов сортировки обменами и сортировки простыми вставками в тех случаях, когда перемещение элемента оказывается существенно более сложным делом, чем сравнение элементов. Использовать это при выполнении следующих заданий.
- Дана действительная матрица размера
n x m; упорядочить (переставить) строки матрицы:
-
а) по неубыванию значений первых элементов строк;
б) по невозрастанию сумм элементов строк;
в) по неубыванию значений наименьших элементов строк;
г) по невозрастанию значений наибольших элементов строк.
- В заданиях б), в), г) разрешается дополнительно определить числовой
массив a1, ..., an.
631 Пусть дан упорядоченный по неубыванию массив целых или действительных чисел a1 ≤ a2 ≤ ... ≤ an и пусть дано некоторое число b (соответственно целое или действительное), для которого нужно найти такое место среди чисел a1, ..., an, чтобы после вставки числа b на это место упорядоченность не нарушилась. Если вследствие равенства между собой некоторых элементов массива число b можно вставлять на разные места, то требуется определить ближайшее к началу массива место. Эта задача называется задачей поиска места элемента. Для b имеется n + 1 возможность: b ≤ a1, a1 < b ≤ a2, ..., an-1 < b ≤ an, an < b, и решением задачи поиска места элемента b будет соответственно одно из чисел 1, ..., n + 1. Для решения задачи полезен алгоритм, который называется алгоритмом деления пополам: взять первоначально 1 и n + 1 в качестве границ поиска места элемента; далее, до тех пор, пока границы не совпадут, шаг за шагом сдвигать эти границы следующим образом: сравнить b с as, где s-целая часть среднего арифметического границ; если as < b, то заменить прежнюю нижнюю границу на s + 1, а верхнюю оставить без изменения, иначе оставить без изменения нижнюю границу, а верхнюю заменить на s; когда границы совпадут, став равным некоторому числу t, выполнение вышеописанного алгоритма закончится с результатом t. (Число сравнений, требуемых этим алгоритмом, не превосходит [log2(n + 1)] + 1).
-
а) Даны действительные числа a1, ..., an, b1, ..., bm
(a1 ≤ a2 ≤ ... ≤ an). Получить натуральные числа
k1, ..., km такие, что ki-это решение задачи поиска места
bi среди a1, ..., an (i = 1, ..., m). Применить алгоритм деления пополам.
б) Таблица выигрышей денежной лотереи представлена массивом выигравших номеров a1, ..., an и массивом выигрышей в рублях p1, ..., pn (pi-это выигрыш, выпавший на номер ai (i = 1, ..., n)). Определить суммарный выигрыш, выпавший на билеты с номерами b1, ..., bm. Применить алгоритм деление пополам.
в) Пусть место некоторого числа b среди упорядоченных по неубыванию a1, ..., an выбирается как наиболее удаленное от начала последовательности место, на которое можно вставить это число, не нарушая этим упорядоченности по неубыванию. Внести изменение в описание алгоритма деления пополам и соответственно дать новое решение задания а), сформулированного выше.
632 Даны действительные числа a1, ..., an, p, натуральное число k (a1 ≤ a2 ≤ ... ≤ an, k ≤ n). Удалить из a1, ..., an элемент с номером k (т.е. ak) и вставить элемент, равный p, так, чтобы не нарушилась упорядоченность.
633 Алгоритм упорядочения простыми вставками (см. алгоритм в) в задаче 628) можно изменить следующим образом: место, на которое надо вставить ai в уже упорядоченную совокупность ai, ..., ai-1, определяется алгоритмом деления пополам (см. задачу 631). Получится новый алгоритм сортировки, который называется алгоритмом сортировки бинарными вставками (слова"бинарная вставка" следует понимать как "вставка делением пополам"). Этот алгоритм требует всего около n log2n сравнением элементов. Написать программу, реализующую этот алгоритм.
634 Даны целые числа a1, ..., an. Получить в порядке возрастания все различные числа, входящие в a1, ..., an. Здесь удобно воспользоваться алгоритмом сортировки вставками (если n велико, то лучше применить бинарные вставки; если n сравнительно мало, скажем, n<50, то можно обойтись и простыми вставками). В процессе сортировки следует отбрасывать элементы, уже встречавшиеся раньше. Если в результате поиска места ai в упорядоченной совокупности a1, ..., ak (k < i) обнаружится, что среди a1, ..., ak есть элемент, равный ai, то следует перейти к рассмотрению ai + 1 без изменения a1, ..., ak.
635 Даны действительные числа c1, ..., cp, d1, ..., dg(c1 ≤ c2 ≤ ... ≤ cp, d1 ≤ d2 ≤ ... ≤ dg). Внести единую упорядоченность в c1, ..., cp, d1, ..., dg, получив f1, f2, ..., fp + g такие, что f1 ≤ f2 ≤ ... ≤ fp + g. Число сравнений не должно превосходить p + g.
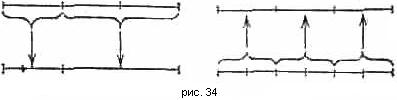
636 Алгоритм фон Неймана упорядочения массива a1, ..., an по неубыванию (алгоритм сортировки слияниями) основан на многократных слияниях уже упорядоченных групп элементов массива (см. предыдущую задачу). В начале весь массив рассматривается как совокупность упорядоченных групп по одному элементу в каждом. Слиянием соседних групп получаем упорядоченные группы, каждая из которых содержит два элемента (кроме, может быть, последней группы, которой не нашлось парной). Далее, упорядоченные группы укрупняются тем же способом и т. д. Здесь приходится оперировать не только с массивом a1, ..., an, но и с вспомогательным массивом b1, ..., bn (первоначальные значения его элементов не играют роли). Рис. 34 демонстрирует два последовательных этапа укрупнения: массивы a1, ..., an и b1, ..., bn представлены в виде отрезков, которые разбиты на части, изображающие упорядоченные группы. Число упорядоченных групп убывает, следовательно, настанет такой момент, когда в массиве a1, ..., an или b1, ..., bn будет содержаться только одна упорядоченная группа. А это означает, что массив упорядочен. Для слияния двух упорядоченных групп, содержащих соответственно p и g элементов, достаточно произвести не более p + g сравнений. Следовательно, для одного этапа укрупнения достаточно произвести не более n сравнений. Столько же требуется на одном этапе и перемещений. Можно показать, что алгоритм фон Неймана требует в целом приблизительно n log2n сравнений и столько же перемещений. Из рассмотренных до сих пор алгоритмов только алгоритм сортировки бинарными вставками требовал столь небольшого числа сравнений. Онако алгоритм фон Неймана выгодно отличается от последнего алгоритма тем, что требует меньше перемещений элементов a1, ..., an (хотя и требует дополнительного массива b1, ..., bn). Написать программу, реализующую алгоритм фон Неймана.
638 На преобразовании массива, описанном в предыдущей задаче, основывается следующий рекурсивный алгоритм сортировки (так называемая быстрая сортировка). Если массив содержит не более одного элемента, то он упорядочен. Иначе применяем к нему преобразование, описанное в предыдущей задаче, и определяем результат применения алгоритма быстрой сортировки к a1, ..., an следующим образом: вначале идет первая группа элементов, упорядоченная с помощью алгоритма быстрой сортировки, затем без изменения тот элемент, который разделял первую и вторую группы элементов, затем вторая группа элементов, упорядоченная с помощью алгоритма быстрой сортировки. Этот алгоритм не использует дополнительного массива и требует в среднем приблизительно nlog2n сравнений и столько же перемещений элементов. Правда, это лишь среднее число: в худшем случае число соавнений может достигать n(n-1)/2; кроме того, алгоритм быстрой сортировки содержит рекурсии.
Написать программу, реализующую алгоритм быстрой сортировки.
639 На преобразовании массива, описанном в задаче 637, основывается также следующий алгоритм поиска значения k-го по величине элемента массива a1, ..., an (т. е. того элемента, который бы занял место с номером k после упорядочения массива). Пусть в результате преобразования, описанного в задаче 637, первый элемент занял p-е место; если k = p, то поиск закончен; если k < p, то надо перейти к поиску k - го по величине элемента в начальной группе элементов, содержащей p-1 элемент (задача упростилась, так как p - 1 < n); если же k > p, то надо перейти к поиску (k - p) - го по величине элемента во второй группе элементов (задача упростилась, так как n - p < n). Этот алгоритм не содержит рекурсий. Не пользуясь рекурсиями, написать программу, реализующую этот алгоритм.
640 Нетрудно заметить, что алгоритм, описанный в предыдущей задаче, фактически позволяет найти не только k-й по величине элемент, но и дополнительно 1 - й, 2 - й, ..., (k - 1) - й элементы, хотя и в неупорядоченном виде. Основываясь на этом, выполнить следующие задания :
-
а) В массиве a1, ..., a2m + 1 найти (m + 1) - й по величине элемент (это так
называемая медиана массива a1, ..., a2m + 1) и группу элементов с первыми
m значениями.
б) Вновь решить задачу 170, положив для этого k = 4.
641 Алгоритм сортировки обменами (см. алгоритм б) в задаче 628) также имеет свои достоинства. Рассмотрим следующий пример. Пусть слова, которые можно выделить в массиве символов a1, ..., an (см. задачу 269), требуется представить в лексикографическом порядке. Так как разные слова могут иметь разную длину, то без больших затруднений можно менять местами только слова, стоящие рядом. Но алгоритм сортировки обменами и предписывает только такие обмены. Эта задача не является, конечно, задачей сортировки массива, но тем не менее алгоритм сортировки обменами оказывается здесь полезным. Написать программу, предполагая, что длина слова не превосходит пятнадцати.
642 Алгоритм б), сформулированный в задаче 628 , - это, строго говоря, лишь один из алгоритмов сортировки обменами. Он иногда называется алгоритмом пузырька. Есть и другие алгоритмы, которые естественно отнести к алгоритмам сортировки обменами. Приведем пример такого алгоритма. Последовательным просмотром чисел a1, ..., an найти наименьшее i такое, что ai > ai + 1. Поменять ai и ai + 1 местами и возобновить просмотр с начала массива. Когда не удастся найти такое i, массив будет упорядочен нужным образом. Написать программу, реализующую этот алгоритм.
643 Рассмотреть все алгоритмы сортировки, сформулированные в этом параграфе, и указать достоинства и недостатки кажлого из них. Необходимо помнить, что в случае небольших массивов те алгоритмы, которые сформулировнны в задаче 628, дают вполне удовлетворительное решение задачи. При больших n требуется тщательно изучить все особенности конкретной ситуации и, исходя из этого, подобрать алгоритм. Задачи сортировки массивов возникают не только в связи с числовыми массивами. Тип элементами может быть довольно сложным, и надо учитывать, во что обходится сравнение и перемещение элементов в том или ином случае.
644 Даны пять попарно различных чисел a, b, c, d, e. Упорядочить их по возрастанию, используя для этого не более семи сравнений.
645 Даны действительные числа a1, ..., an. Получить попарно различные целые i1, ..., in такие, что 1 ≤ ik ≤ n, k = 1, ..., n и ai1 ≥ ai2 ≥ ... ≥ ain.
646 Даны натуральное число n, целые числа a1, ..., an. Найти наибольшее значение, встречающееся в последовательности a1, ..., an, после выбрасывания из нее
-
а) одного из членов со значением max (a1, ..., an);
б) всех членов со значением max (a1, ..., an) - здесь предполагается, что не все числа a1, ..., an равны между собой.
647 Даны натуральное число n, действительные числа a1, ..., an. Требуется найти max (a1, ..., an) и min (a1, ..., an). Рассмотрим два алгоритма решения этой задачи. Первый алгоритм. Шаг за шагом получить пары max (a1, ..., ai), min (a1, ..., ai) (i = 1, ..., n). При этом, чтобы получить max (a1, ..., ai + 1), min (a1, ..., ai + 1), сравнивается ai + 1 с max (a1, ..., ai), а затем, если ai + 1 < max (a1, ..., ai), дополнительно сравнивается ai + 1 с min (a1, ..., ai). Второй алгоритм. Пусть n - четное число, т.е. n = 2k. Тогда шаг за шагом получать max (a1, ..., a2l), min (a1, ..., a2l) (l = 1, ..., k). При этом, чтобы получить max (a1, ..., a2l + 2), min (a1, ..., a2l + 2), вначале сравниваются между собой a2l + 1, a2l + 2 и max (a2l + 1, a2l + 2) сравнивается с max (a1, ..., a2l), а min(a2l + 1, a2l + 2) - с min (a1, ..., a2l). Если n -нечетное число, то потребуется еще дополнительный шаг: сравнение последнего элемента и an с max (a1, ..., an-1) и, возможно, с min (a1, ..., an-1).
- Сколько сравнений в худшем
случае потребует первый алгоритм и сколько - второй? Написать прграмму, реализующую второй алгоритм.
(Заметим, что второй алгоритм дает еще одно решение задачи 230.)
648 Даны натуральные числа a1, ..., an. Пусть a1, ..., an - перестановка чисел 1, ..., n. Получить натуральные r1, ..., rn такие, что rai = i для i = 1, ..., n.
649 Решить задачи 646, 647, предполагая, что числа a1, ..., an являются компонентами данного файла. При этом значение n неизвестно заранее.
650 Число компонент файла f, компонентами которого являются целые числа, кратно десяти. Переписать компоненты файла f в файл q, изменяя порядок чисел в каждой десятке так, чтобы
-
а) вначале шли отрицательные числа десятки, а за ними - неотрицательные;
б) вначале шли числа, делящиеся на 3, затем числа, дающие при делении на 3 остаток 1, затем числа, дающие при делении на 3 остаток 2.
- Порядок самих десяток должен быть сохранен.
651 Рассматриваются слова (см. задачу 269), содержащиеся в символьных файлах f1 и f2. Известно, что число символов в словах не превосходит шестнадцати. Известно также, что слова в файле f2 идут в лексикографическом порядке и их число равно пятидесяти. Выяснить, сколько раз каждое из слов файла f2 встречается в файле f1. Для решения задачи переписать слова, содержащиеся в файле f2, в массив и последовательно применять метод деления пополам (см. задачу 631).
652 Пусть файлы c и d с компонентами, являющимися действительными или целыми числами, упорядочены по невозрастанию компонент. Требуется собрать компоненты файлов c и d в упорядоченном виде в файле f (ср. c задачей 635). Количество сравнений не должно превосходить p + g, где p и g - число компонент в файлах c и d.
653 Пусть a и b - файлы, k - натуральное число. Будем говорить, что файлы a и b согласованно k - упорядочены, если
-
1) в каждом из файлов a и b первые k компонент, следуящие за ними k компонент и т.д. образуют
упорядоченные группы; последняя группа файла (тоже упорядоченная) может быть неполной, т.е.
содержать менее k компонент, но при этом только один из файлов a и b может иметь не полную
последнюю группу;
2) число упорядоченных групп файла a отличается от числа упорядоченных групп файла b не более чем на единицу;
3) если в одном файле число упорядоченных групп меньше на единицу, чем в другом, то не полной может быть только последняя группа более длинного файла.
- Компоненты двух согласованно k - упорядоченных файлов a и b можно
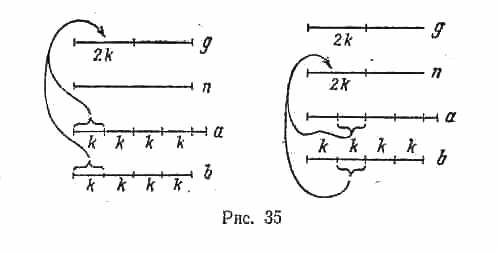
разместить в файлах g и h так, что g и h, будут согласованно 2k - упорядочены. Это делается с помощью
описанных в предыдущей задаче слияний; при этом результаты слияния попеременно размещаются то в файле g,
то в файле h. Рисунок 35 демонстрирует происходящее при первых двух слияниях. Файлы представлены в виде
отрезков, части которых изображают упорядоченные группы с указанным числом компонент.
-
Завершить описание этого алгоритма, рассмотрев его заключительную стадию. Доказать,
что файлы g и h действительно будут согласованно 2k - упорядоченны. Реализовать этот алгоритм в виде
программы.
- Этот алгоритм очень похож
на алгоритм фон Неймана для массивов (см. задачу 636) и тоже относится к
алгоритмам сортировки слияниями.
- Реализовать этот алгоритм в виде программы.
655 Пусть файлы а и b, компоненты которых являются целыми числами, упорядочены по неубыванию. Получить в файле с все числа файлов а и b без повторений. Файл с должен быть упорядочен по возрастанию.
656 Дан файл f, компоненты которого являются целыми числами. Получить в файле g все нечётные числа, входящие в файл f. Числа в файле g должны следовать:
-
а) в порядке невозрастания;
б) в порядке убывания, без повторений.
657 Дан символьный файл f, компоненты которого - малые латинские буквы и пробелы. Слова (см. задачу 269) файла f имеют не более шестнадцати букв. Записать эти слова в файл g в лексикографическом порядке.
* В задачах 628 - 648 этого параграфа существенно, что данные рассматриваются в программе как массив; в задачах 649 - 657 рассматриваются файлы, и это усложняет некоторые алгоритмы.
 Предыдущая глава
Предыдущая глава