785 У кроликов чёрная окраска (определяемая аллем В) доминирует над белой
(определяемой аллем b). Даны сочетания аллей B и b в генотипах кроликов-родителей, каждое из сочетаний -
это ВВ,Вb или bb. Используя законы Менделя, перечислить возможности для сочетаний аллей В и b в генотипе
потомка первого поколения (F1) этой пары. Вместе с каждым возможным сочетанием указать окраску
потомка.
786 Каждый из двух подвергнутых скрещиванию сортов гороха имел либо желтые, либо зелёные семядоли. Известно, что желтая окраска семядолей (аллель R) доминирует над зелёной (аллель r). Среди растений F1 (см. предыдущую задачу) имелось n с желтыми семядолями и m с зелёными (n ≥ 0, m ≥ 0). Используя законы Менделя, перечислить наиболее вероятные возможности сочетаний аллей R и r в генотипах родителей.
787 Вернёмся к сортам гороха сжелтыми (аллель R) и зелёными (аллель r) семядолями (см. предыдущую задачу). Были подвергнуты скрещиванию два растения, одно из которых имело зелёные семядоли. В результате скрещивания получили m растений F1 (см.задачу 785) с желтыми семядолями и n-с зелёными (n ≥ 0, m ≥ 0). Используя законы Менделя, указать наиболее вероятное сочетание аллей R и r в генотипе второго родителя и в генотипах каждого из растений F1.
788 Два сорта пшеницы различают устойчивостью к определённому пестицыду (ядохимикату). Делается предположение, что в гетерозиготном растений проявляет своё действие только один аллель-устоичивости или неустойчивости к данному пестицыду, т.е. имеет место явление доминирования. Взяты два растения-одно устоичивое, другое неустойчивое. В результате скрещивания этих растений появилось несколько устойчивых растений F1 и несколько неустойчивых. Проведены с двумя растениями F1 ,из которых одно было устойчивым к пестициду,а другое-нет. Результаты этих четырёх возвратных скрещиваний известны и записаны четырьмя парами неотрицательных целых чисел (первое число пары указывает количество растений, устойчивых к пестициду, второе-неустойчивых). Подтверждают ли результаты проведённых опытов гипотезу о доминировании? Если да, то какой из признаков (устойчивость или неустойчивость) является доминируюшим?
789 "Контакты первого и второго порядка в эпидемиологии". Предположим, что k человек заболели инфекционной болезнью. Вторую группу из L человек опросили с целью выяснения, кто из них имел контакт с больными. Заием опросили третью группу из m человек, чтоб выяснить контакт с кем-нибудь из L человек второй группы. Результаты первого опроса записаны в виде матрицы |aij| i=1, ..., k; j=1, ..., l так, что aij = 1, если j-й человек второй группы находился в контакте с i-м больным из первой группы, и aij = 0 в противном случае. Аналогично определена матрица |bij| i=1, ..., l; j=1, ..., m: bij = 1, если j-й человек третьей группы находился в контакте с i-м человеком из второй группы, и bij = 0 в противном случае. Эти две маирицы описывают схему контактов первого порядка между группами. Могут представлять интерес непрямые контакты, или, иначе говоря, контакты второго порядка между людьми третьей группы и больными первой группы. Исходя из двух упомянутых матриц, получить маирицу |cij| i=1, ..., k; j=1, ..., m контактов второго порядка.
790 Реакция организма на лекарство через n часов после инъекции выражается показателем rn, измеряемым в подходящих еденицах. Экспериментально установлено, что для лекарственных препаратов некоторой группы показатель реакции есть rn = αrn-1 + 0.4rn, где r0 = 1, a α - меньше единицы данное положительное число, характеризующее конкретный препорат группы. Определить, через сколько часов наступает максимальная реакция на введение препарата. После скольких часов реакция понизится ниже 50% первоначального уровня r0?
791 В процесе лечебного голодания вес пациента за 30 дней снизился с 96 до 70 кг. Было установлено, что ежедневные потери веса пропорциональны весу тела. Вычислить, чему равен вес пациента через k дней после начала голодания для k = 1,2,...,29.
792 Если культура клеток в питательной среде растёт, не подвергаясь внешним воздействиям, то прирост массы в течении (n+1)-го часа оказывается вдвое больше прироста в течении n-го часа. Однако в исследовательских целях к растушей массе по истечению каждого часа добовляется по 2г культуры. Дано натуральное число k. Найти массу xk в коце k-го часа исследования если перваночально было взято 3г.(Исходя из предположения, что при отсутствии внешнего воздействия масса xn в конце n-го часа исследования удовлетворяет соотношению xn = αxn-1 для некоторой постоянной величены α)
793 В одном большом стаде, состояшем из животных одного возраста и пола, рост животных, измеренный в сантиметрах, колеблется от k до l (даны натуралиные числа).
794 Числа Фибоначчи U0, U1, ... (см.задачу 144) получили название в честь итальянского математика Леонардо Фибоначчи, который ввёл их для описания численности поколений животных (без учёта смертности). Предпологается,что каждая пара животных некоторого вида приносит ежегодно приплод в одну пару животных(самку исамца), которые в свою очередь начинают давать приплод через два года после рождения. Если имеется одна пара новорожденных животных, то как можно показать по прошествии n лет будет иметься Un+1 пар животных. Внести в эту модель уточнение, касающееся смертности. Считать, что продолжительность жизни животного:
795 Для описания происходящего со временем изменения численности популяции удобно рассматривать распределение популяции по возрастным группам (в первую группу попадают все особи в возрасте до года, во вторую- все те не попавшие в первую группу особи, возраст которых меньше двух лет, и т.д.). Пусть в первую возрастную группу входит p1 особей, во вторую - p2 особей и т.д. Смертность весьма упрощенно можно учесть, положив, что все особи вымирают, находясь в n-й возрастной группе, где n- некоторое фиксированное натуральное число. Ясно, что общее число особей в популяции есть p1 +...+ pn. Для каждой возрастной группы имеется свой коэффициент рождаемости; если коэффициенты для рассматриваемых возрастных групп соответственно равны b1, ..., bn, то годовой прирост, обусловленный присутствием в популяции i-й возрастной группы с численностью pi, есть bipi. Таким образом, годовой прирост по всей популяции есть b1p1 +...+ bnpn. В то же время особи, принадлежащие i-й возрастной группе, через год перейдут в (i+1)-ю возрастную групу(i=1,...,n-1), а особи, принадлежащие n-й возрастной группе, вымрут в течение года. Поэтому через год распределение популяции по возрастным группам будет следующим: b1p1 +...+ bnpn ,b1p1 +...+ bnpn.
796 Описанную в предидущей задаче модель изменения численности популяции можно сделать более точной введением, кроме коэффициента рождаемости, ещё и коэффициентов выживания S1, ..., Sn (0 ≤ Si < 1, i = 1, ..., n) для всех возрастных групп: считаем, что если в текущем году j-я возрастная группа имеет числанность pi, то в будующем году (i+1)-я возрастная группа будет иметь численность, равную Si, pi. При этом sn = 0 (так как мы по-прежнему считаем, что возраст особи не превосходит n лет), и фактически можно рассматривать только S1, ..., Sn-1. Годовой прирост за счёт i-й группы в этой модели считается равным biSipi. Коэффициенты выживания, так же как и коэффициенты рождаемости, выводятся на основе многолетних наблюдений за популяциями данного вида.
797 Дополняя модель, которая была описана в предидущей задаче, предположим, что когда численность популяции оказывается к концу года большей, чем некоторое число l, то из-за большой скученности начинается эпидемия, приводящая к понижению вдвое коэффициентов выживания S1, ..., Sn-1 в следующем году.
798 Взаимное влияние некоторых двух конкурирующих видов на размер xn, yn их популяций в n-м году описывается системой
799 Даны натуральные числа n, a1, ..., an, отражающие наблюдения за лесным муравейником. Вначале было отловлено 100 рабочих муравьёв, все они были помечены и выпущены на волю. Далее, в течении n дней повторялось следующее: отлавливалось по 100 рабочих муравьёв, подсчитывалось число помеченных среди них (ai - количество помеченных муравьёв среди отловленных в i-й день, i=1,...,n), помечались непомеченные муравьи, находящиеся в этой сотне, затем все 100 муравьёв вупускались на волю. Требуется подсчитать (приблезительно) число рабочих муравьёв в этом муравейнике.
800 Эта задача является продолжением предидущей. Через год наблюдения над муравейником были возобновлены. Вновь сначала было отловлено 100 рабочих муравьёв и все они были помечены новой, отличимой от прошлогодней меткой и выпущены на волю. Затем в течение n дней повторялось следующее: отлавливалось по 100 рабочих муравьёв, подсчитывалось число помеченных только прошлогодней меткой, только новой меткой и обеими метками (в i-й день фиксировались соответственно числа ai, biuci), затем помечались муравьи этой сотни, ещё не помеченные меткой этого года, и все 100 муравьёв выпускались на волю.
801 "Зависимость веса от роста". Часто пытаются "уложить" некоторые экспериментальные или статистмческие данные в некоторую простую формулу. Пусть, например, обследовано n взрослых людей с нормальным телосложением и измерен рост (в см) xi вес (в кг) yi, у каждого из них. Можно пытаться на основании этих измерений получить формулу вида y=ax+b, выражающую вес y через рост x. Конечно, трудно расчитывать на то, что для каких-либо конкретных a и b будут с абсалютной точностью выполнены все n равенств yi = axi + b. Но не трудно найти a и b такие, что величина f(a,b), равная (ax1 + b - y1)2 + (ax2 + b - y2)2 + ... + (axn + b - yn)2, имеет наименьшее из возможных значений (рис.57). Для выполнения этого условия достаточно, чтобы *)
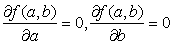 .
.
Последние равенства дают два линейных уравнения для определения a и b(это частный случай метода наименьших квадратов, принадлежащего Гауссу):
*) Пусть g(t1, ..., tk) - функция указанных действительных переменных, ∂g/∂ti, т.е. результат дифференцирования g по ti, при котором все величины, кроме ti считаются постоянными.
786 Каждый из двух подвергнутых скрещиванию сортов гороха имел либо желтые, либо зелёные семядоли. Известно, что желтая окраска семядолей (аллель R) доминирует над зелёной (аллель r). Среди растений F1 (см. предыдущую задачу) имелось n с желтыми семядолями и m с зелёными (n ≥ 0, m ≥ 0). Используя законы Менделя, перечислить наиболее вероятные возможности сочетаний аллей R и r в генотипах родителей.
787 Вернёмся к сортам гороха сжелтыми (аллель R) и зелёными (аллель r) семядолями (см. предыдущую задачу). Были подвергнуты скрещиванию два растения, одно из которых имело зелёные семядоли. В результате скрещивания получили m растений F1 (см.задачу 785) с желтыми семядолями и n-с зелёными (n ≥ 0, m ≥ 0). Используя законы Менделя, указать наиболее вероятное сочетание аллей R и r в генотипе второго родителя и в генотипах каждого из растений F1.
788 Два сорта пшеницы различают устойчивостью к определённому пестицыду (ядохимикату). Делается предположение, что в гетерозиготном растений проявляет своё действие только один аллель-устоичивости или неустойчивости к данному пестицыду, т.е. имеет место явление доминирования. Взяты два растения-одно устоичивое, другое неустойчивое. В результате скрещивания этих растений появилось несколько устойчивых растений F1 и несколько неустойчивых. Проведены с двумя растениями F1 ,из которых одно было устойчивым к пестициду,а другое-нет. Результаты этих четырёх возвратных скрещиваний известны и записаны четырьмя парами неотрицательных целых чисел (первое число пары указывает количество растений, устойчивых к пестициду, второе-неустойчивых). Подтверждают ли результаты проведённых опытов гипотезу о доминировании? Если да, то какой из признаков (устойчивость или неустойчивость) является доминируюшим?
789 "Контакты первого и второго порядка в эпидемиологии". Предположим, что k человек заболели инфекционной болезнью. Вторую группу из L человек опросили с целью выяснения, кто из них имел контакт с больными. Заием опросили третью группу из m человек, чтоб выяснить контакт с кем-нибудь из L человек второй группы. Результаты первого опроса записаны в виде матрицы |aij| i=1, ..., k; j=1, ..., l так, что aij = 1, если j-й человек второй группы находился в контакте с i-м больным из первой группы, и aij = 0 в противном случае. Аналогично определена матрица |bij| i=1, ..., l; j=1, ..., m: bij = 1, если j-й человек третьей группы находился в контакте с i-м человеком из второй группы, и bij = 0 в противном случае. Эти две маирицы описывают схему контактов первого порядка между группами. Могут представлять интерес непрямые контакты, или, иначе говоря, контакты второго порядка между людьми третьей группы и больными первой группы. Исходя из двух упомянутых матриц, получить маирицу |cij| i=1, ..., k; j=1, ..., m контактов второго порядка.
790 Реакция организма на лекарство через n часов после инъекции выражается показателем rn, измеряемым в подходящих еденицах. Экспериментально установлено, что для лекарственных препаратов некоторой группы показатель реакции есть rn = αrn-1 + 0.4rn, где r0 = 1, a α - меньше единицы данное положительное число, характеризующее конкретный препорат группы. Определить, через сколько часов наступает максимальная реакция на введение препарата. После скольких часов реакция понизится ниже 50% первоначального уровня r0?
791 В процесе лечебного голодания вес пациента за 30 дней снизился с 96 до 70 кг. Было установлено, что ежедневные потери веса пропорциональны весу тела. Вычислить, чему равен вес пациента через k дней после начала голодания для k = 1,2,...,29.
792 Если культура клеток в питательной среде растёт, не подвергаясь внешним воздействиям, то прирост массы в течении (n+1)-го часа оказывается вдвое больше прироста в течении n-го часа. Однако в исследовательских целях к растушей массе по истечению каждого часа добовляется по 2г культуры. Дано натуральное число k. Найти массу xk в коце k-го часа исследования если перваночально было взято 3г.(Исходя из предположения, что при отсутствии внешнего воздействия масса xn в конце n-го часа исследования удовлетворяет соотношению xn = αxn-1 для некоторой постоянной величены α)
793 В одном большом стаде, состояшем из животных одного возраста и пола, рост животных, измеренный в сантиметрах, колеблется от k до l (даны натуралиные числа).
-
а) Пусть m и n-данные натуральные числа такие, что k ≤ m < n ≤ l.
Каких животных в стаде больше-с ростом, близким к m см, или с ростом, близким к n см?
б) Если r-количество пищи, потребляемое в сутки животным сростом k, то каково количество пищи, потребляемое в сутки животным сростом l? Если s-количество шерсти, состригаемой ежегодно с животного с ростом k, то сколько приблезительно шерсти можно ежегодно состригать с животного с ростом l? (Предпологается, что густота и длина шерсти не зависят от рста.)
794 Числа Фибоначчи U0, U1, ... (см.задачу 144) получили название в честь итальянского математика Леонардо Фибоначчи, который ввёл их для описания численности поколений животных (без учёта смертности). Предпологается,что каждая пара животных некоторого вида приносит ежегодно приплод в одну пару животных(самку исамца), которые в свою очередь начинают давать приплод через два года после рождения. Если имеется одна пара новорожденных животных, то как можно показать по прошествии n лет будет иметься Un+1 пар животных. Внести в эту модель уточнение, касающееся смертности. Считать, что продолжительность жизни животного:
-
а) 5 лет;
б) m лет, где m-данное натуральное число.
- Вычислить количество пар животных, которые будет иметься по прошествию
сорока в n лет (n-данное натуральное число).
795 Для описания происходящего со временем изменения численности популяции удобно рассматривать распределение популяции по возрастным группам (в первую группу попадают все особи в возрасте до года, во вторую- все те не попавшие в первую группу особи, возраст которых меньше двух лет, и т.д.). Пусть в первую возрастную группу входит p1 особей, во вторую - p2 особей и т.д. Смертность весьма упрощенно можно учесть, положив, что все особи вымирают, находясь в n-й возрастной группе, где n- некоторое фиксированное натуральное число. Ясно, что общее число особей в популяции есть p1 +...+ pn. Для каждой возрастной группы имеется свой коэффициент рождаемости; если коэффициенты для рассматриваемых возрастных групп соответственно равны b1, ..., bn, то годовой прирост, обусловленный присутствием в популяции i-й возрастной группы с численностью pi, есть bipi. Таким образом, годовой прирост по всей популяции есть b1p1 +...+ bnpn. В то же время особи, принадлежащие i-й возрастной группе, через год перейдут в (i+1)-ю возрастную групу(i=1,...,n-1), а особи, принадлежащие n-й возрастной группе, вымрут в течение года. Поэтому через год распределение популяции по возрастным группам будет следующим: b1p1 +...+ bnpn ,b1p1 +...+ bnpn.
-
Даны натуральные числа n,m, действительные числа b1, ..., bn, неотрицательные
целые числа p1 +...+ pn. Считая, что p1 +...+ pn- первоначально
зарегистрированное распределение популяции по возрастным группам, а b1, ..., bn -
коэффициенты рождаемости для возрастных групп, определить общую численность популяции через m лет.
796 Описанную в предидущей задаче модель изменения численности популяции можно сделать более точной введением, кроме коэффициента рождаемости, ещё и коэффициентов выживания S1, ..., Sn (0 ≤ Si < 1, i = 1, ..., n) для всех возрастных групп: считаем, что если в текущем году j-я возрастная группа имеет числанность pi, то в будующем году (i+1)-я возрастная группа будет иметь численность, равную Si, pi. При этом sn = 0 (так как мы по-прежнему считаем, что возраст особи не превосходит n лет), и фактически можно рассматривать только S1, ..., Sn-1. Годовой прирост за счёт i-й группы в этой модели считается равным biSipi. Коэффициенты выживания, так же как и коэффициенты рождаемости, выводятся на основе многолетних наблюдений за популяциями данного вида.
- Считая заданными S1, ..., Sn-1, вновь рассмотреть
задачу расчёта численности популяции через m лет.
797 Дополняя модель, которая была описана в предидущей задаче, предположим, что когда численность популяции оказывается к концу года большей, чем некоторое число l, то из-за большой скученности начинается эпидемия, приводящая к понижению вдвое коэффициентов выживания S1, ..., Sn-1 в следующем году.
- Считая l заданным числом,
вновь рассмотреть задачу расчёта численности популяции через m лет.
798 Взаимное влияние некоторых двух конкурирующих видов на размер xn, yn их популяций в n-м году описывается системой
-
xn+1 = 2xn - yn,
yn+1 = -xn + 2yn.
- Пусть x0 = a, y0 = b (a ≠ b), где a и b -
данные числа. Найти численности обоих видов за все годы, предшествующие полному вымиранию одного из них.
799 Даны натуральные числа n, a1, ..., an, отражающие наблюдения за лесным муравейником. Вначале было отловлено 100 рабочих муравьёв, все они были помечены и выпущены на волю. Далее, в течении n дней повторялось следующее: отлавливалось по 100 рабочих муравьёв, подсчитывалось число помеченных среди них (ai - количество помеченных муравьёв среди отловленных в i-й день, i=1,...,n), помечались непомеченные муравьи, находящиеся в этой сотне, затем все 100 муравьёв вупускались на волю. Требуется подсчитать (приблезительно) число рабочих муравьёв в этом муравейнике.
800 Эта задача является продолжением предидущей. Через год наблюдения над муравейником были возобновлены. Вновь сначала было отловлено 100 рабочих муравьёв и все они были помечены новой, отличимой от прошлогодней меткой и выпущены на волю. Затем в течение n дней повторялось следующее: отлавливалось по 100 рабочих муравьёв, подсчитывалось число помеченных только прошлогодней меткой, только новой меткой и обеими метками (в i-й день фиксировались соответственно числа ai, biuci), затем помечались муравьи этой сотни, ещё не помеченные меткой этого года, и все 100 муравьёв выпускались на волю.
- Требуется выдвинуть
разумные гипотезы относительно числа среди них новых рабочих муравьёв и количестве прошлогодних.
Исходные данные задачи: k, l, n, a1, b1, c1, a2,
b2, c2, ..., an, bn, cn, где k-число рабочих муравьёв,
помеченных в прошлом году, l-предположительное общее число рабочих муравьёв в прошлом году. Смысл остальных
чисел разъяснён выше.
801 "Зависимость веса от роста". Часто пытаются "уложить" некоторые экспериментальные или статистмческие данные в некоторую простую формулу. Пусть, например, обследовано n взрослых людей с нормальным телосложением и измерен рост (в см) xi вес (в кг) yi, у каждого из них. Можно пытаться на основании этих измерений получить формулу вида y=ax+b, выражающую вес y через рост x. Конечно, трудно расчитывать на то, что для каких-либо конкретных a и b будут с абсалютной точностью выполнены все n равенств yi = axi + b. Но не трудно найти a и b такие, что величина f(a,b), равная (ax1 + b - y1)2 + (ax2 + b - y2)2 + ... + (axn + b - yn)2, имеет наименьшее из возможных значений (рис.57). Для выполнения этого условия достаточно, чтобы *)
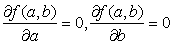 .
.Последние равенства дают два линейных уравнения для определения a и b(это частный случай метода наименьших квадратов, принадлежащего Гауссу):
-
(x12 + ... + xn2)a + (x1 + ...
+ xn)b = x1y1 + ... + xnyn,
(x1 + ... + xn)a + nb = y1 + ... + yn.
- Даны действительные числа x1, ..., xn,
y1, ..., yn. Получить указанные a и b. По поводу этой задачи сделаем следующее
замечание. Действительно, этим способом можно получить некоторые a и b; более того, считается, например,
что для мужчин с нормальным телосложением a ≈ 1, b ≈ - 100. Однако значительно более точную
формулу можно, видимо, получить, используя не многочлен первой степени ax + b, а многочлен третьей
степени ax3 + bx2 + cx + d (ср. с задачей 793б). Этот многочлен тоже можно искать
методом наименьших квадратов.
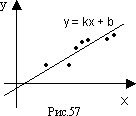
*) Пусть g(t1, ..., tk) - функция указанных действительных переменных, ∂g/∂ti, т.е. результат дифференцирования g по ti, при котором все величины, кроме ti считаются постоянными.
 Предыдущая глава
Предыдущая глава