822 Дан номер года. Указать число дней в этом году.
823 Даны натуральные числа n, m (n ≤ m). Определить, сколько из чисел n, n + 1, ..., m являются номерами високосных годов.
824 Даны натуральные числа a, b, c, которые обозначают число, месяц и год, например 1, 4, 1901 - 1 апреля 1901 года. Получить тройку чисел, соответствующих следующему дню.
825 Даны натуральные числа a 1, b 1, c 1, a 2, b 2, c 2, которые указывают две даты ( число, месяц, год ). Вычислить:
826 Даны натуральные числа a, b, c, которые обозначают число, месяц и год.
827 Даны натуральные числа a, b, которые обозначают число и месяц. На какой день недели приходится эта дата, если год - невисокосный, 1 января этого года - среда ?
828 << Вечный календарь >>. Даны натуральные числа a, b, c, которые обозначают число, месяц и год. Определить день недели, на который падает указанная дата. При решении этой и некоторых следующих задач можно считать, что исследуемая дата лежит в диапазоне от 1582 до 4902 г г. Как установлено, в этом случае номер дня недели ( воскресенье имеет номер 0, понедельник номер - 1, ..., суббота - номер 6 ) равен остатку от деления на 7 значения выражения [ 2. 6 m - 0. 2 ] + d + y + [ y / 4 ] + [ c / 4 ] - 2 c, где d - номер дня в месяце ( 1, 2, ... ); m - номер месяца в году, нумерация начинается c марта ( март имеет номер 1, апрель - номер 2, ..., декабрь - номер 10, январь и февраль считаются месяцами с номерами 11 и 12 предыдущего года ); y - две младшие цифры года ( 00, ..., 99 ); c - две старшие цифры ( 15, ..., 49 ); [ x ] означает целую часть числа x.
Для создания более универсального календаря, охватывающего все годы можно исользовать непосредственный подсчёт, основанный на том что 1 января 1 года нашей эры было понедельником.
829 Вычислить количество пятниц, приходящихся на 13 - е числа
830 Даны натуральные числа a, b, c, обозначающие дату ( число, месяц, год ) по юлианскому календарю. Расхождение между датами определяется тем, что в юлианском календаре каждый год, номер которого делится на 4, является високосным, и из этого правила нет ни каких исключений.
831 День учителя ежегодно отмечается в первое воскресенье октября. Дано натуральное число n, означающее номер года. Определить число, на которое в октябре указанного года приходится День учителя.
832 В некоторой библиотеке последний четверг каждого месяца - санитарный день. Дано натуральное число n, означающее номер года. Получить по порядку все числа, на которые в январе, феврале, ..., декабре указанного года приходится санитарный день.
833 Земной год продолжается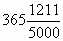 суток. Из
этого следует, что точной была бы такая календарная система, при которой среди 5000 следующих друг за
другом годов имеется 1211 високосных и соответственно 3789 невисокосных. Эта система, основанная на 5000
летних циклах, была бы неудобной в практических отношениях. Задача построения более удобных календарных
систем решается с помощью подходящих дробей ( см. задачу
575). Найти, используя вычислительную машину, все подходящие
дроби числа 1211/5000. Какая именно из этих дробей определяет закон чередования високосных и невисокосных
годов в современном календаре ( четырёхлетние циклы )? Указать так же подходящую дробь, определяющую
закон чередования в календаре Омара Хайяма, в котором рассматривались не четырёхлетние, а тридцатилетние
циклы.
суток. Из
этого следует, что точной была бы такая календарная система, при которой среди 5000 следующих друг за
другом годов имеется 1211 високосных и соответственно 3789 невисокосных. Эта система, основанная на 5000
летних циклах, была бы неудобной в практических отношениях. Задача построения более удобных календарных
систем решается с помощью подходящих дробей ( см. задачу
575). Найти, используя вычислительную машину, все подходящие
дроби числа 1211/5000. Какая именно из этих дробей определяет закон чередования високосных и невисокосных
годов в современном календаре ( четырёхлетние циклы )? Указать так же подходящую дробь, определяющую
закон чередования в календаре Омара Хайяма, в котором рассматривались не четырёхлетние, а тридцатилетние
циклы.
823 Даны натуральные числа n, m (n ≤ m). Определить, сколько из чисел n, n + 1, ..., m являются номерами високосных годов.
824 Даны натуральные числа a, b, c, которые обозначают число, месяц и год, например 1, 4, 1901 - 1 апреля 1901 года. Получить тройку чисел, соответствующих следующему дню.
825 Даны натуральные числа a 1, b 1, c 1, a 2, b 2, c 2, которые указывают две даты ( число, месяц, год ). Вычислить:
-
a) количество дней, прошедших между двумя этими датами;
б) количество полных лет, прошедших между двумя этими датами.
826 Даны натуральные числа a, b, c, которые обозначают число, месяц и год.
-
а) Проверить корректность этой даты ( например, 30 февраля 1900 года - некорректная дата ).
б) Найти номер этого дня с начала года.
в) Определить, сколько полных дней осталось до конца года.
827 Даны натуральные числа a, b, которые обозначают число и месяц. На какой день недели приходится эта дата, если год - невисокосный, 1 января этого года - среда ?
828 << Вечный календарь >>. Даны натуральные числа a, b, c, которые обозначают число, месяц и год. Определить день недели, на который падает указанная дата. При решении этой и некоторых следующих задач можно считать, что исследуемая дата лежит в диапазоне от 1582 до 4902 г г. Как установлено, в этом случае номер дня недели ( воскресенье имеет номер 0, понедельник номер - 1, ..., суббота - номер 6 ) равен остатку от деления на 7 значения выражения [ 2. 6 m - 0. 2 ] + d + y + [ y / 4 ] + [ c / 4 ] - 2 c, где d - номер дня в месяце ( 1, 2, ... ); m - номер месяца в году, нумерация начинается c марта ( март имеет номер 1, апрель - номер 2, ..., декабрь - номер 10, январь и февраль считаются месяцами с номерами 11 и 12 предыдущего года ); y - две младшие цифры года ( 00, ..., 99 ); c - две старшие цифры ( 15, ..., 49 ); [ x ] означает целую часть числа x.
Для создания более универсального календаря, охватывающего все годы можно исользовать непосредственный подсчёт, основанный на том что 1 января 1 года нашей эры было понедельником.
829 Вычислить количество пятниц, приходящихся на 13 - е числа
-
а) XX столетия;
б) столетия с номером n, где n - данное натуральное число.
830 Даны натуральные числа a, b, c, обозначающие дату ( число, месяц, год ) по юлианскому календарю. Расхождение между датами определяется тем, что в юлианском календаре каждый год, номер которого делится на 4, является високосным, и из этого правила нет ни каких исключений.
831 День учителя ежегодно отмечается в первое воскресенье октября. Дано натуральное число n, означающее номер года. Определить число, на которое в октябре указанного года приходится День учителя.
832 В некоторой библиотеке последний четверг каждого месяца - санитарный день. Дано натуральное число n, означающее номер года. Получить по порядку все числа, на которые в январе, феврале, ..., декабре указанного года приходится санитарный день.
833 Земной год продолжается
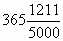 суток. Из
этого следует, что точной была бы такая календарная система, при которой среди 5000 следующих друг за
другом годов имеется 1211 високосных и соответственно 3789 невисокосных. Эта система, основанная на 5000
летних циклах, была бы неудобной в практических отношениях. Задача построения более удобных календарных
систем решается с помощью подходящих дробей ( см. задачу
575). Найти, используя вычислительную машину, все подходящие
дроби числа 1211/5000. Какая именно из этих дробей определяет закон чередования високосных и невисокосных
годов в современном календаре ( четырёхлетние циклы )? Указать так же подходящую дробь, определяющую
закон чередования в календаре Омара Хайяма, в котором рассматривались не четырёхлетние, а тридцатилетние
циклы.
суток. Из
этого следует, что точной была бы такая календарная система, при которой среди 5000 следующих друг за
другом годов имеется 1211 високосных и соответственно 3789 невисокосных. Эта система, основанная на 5000
летних циклах, была бы неудобной в практических отношениях. Задача построения более удобных календарных
систем решается с помощью подходящих дробей ( см. задачу
575). Найти, используя вычислительную машину, все подходящие
дроби числа 1211/5000. Какая именно из этих дробей определяет закон чередования високосных и невисокосных
годов в современном календаре ( четырёхлетние циклы )? Указать так же подходящую дробь, определяющую
закон чередования в календаре Омара Хайяма, в котором рассматривались не четырёхлетние, а тридцатилетние
циклы.
 Предыдущая глава
Предыдущая глава