554 Дано натуральное число n. Получить все пифагоровы тройки натуральных чисел,
каждое из которых не превосходит n, т.е. все такие тройки натуральных чисел a, b, c, что a2 +
b2 = c2 (a ≤ b ≤ c ≤ n).
555 Треугольником Паскаля называется числовой треугольник
1
1 1
1 2 1
1 3 3 1
1 4 6 4 1
.......................................
в котором по краям стоят единицы, а каждое число внутри равно сумме двух стоящих над ним в ближайшей строке сверху. Дано натуральное n. Получить первые n строк треугольника Паскаля.
556 Для чисел Фибоначчи u0, u1, ...(см.задачу 144) справедлива формула Бине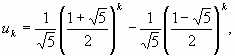 k = 0, 1, ...
k = 0, 1, ...
Так как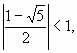 то для больших k выполнено приближенное равенство
то для больших k выполнено приближенное равенство
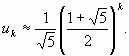
Вычислить и округлить до целого все члены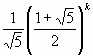 (k = 0, 1, ..., 15). Вычислить u0, u1,
..., u15 по формулам u0 = 0; u1 = 1; uk = uk-1 +
uk-2 (k = 2, 3...) и сравнить результаты.
(k = 0, 1, ..., 15). Вычислить u0, u1,
..., u15 по формулам u0 = 0; u1 = 1; uk = uk-1 +
uk-2 (k = 2, 3...) и сравнить результаты.
557 Дано натуральное число n (n ≥ 2). Найти все меньшие n простые числа, используя решето Эратосфена. Решетом Эратосфена называется следующий способ. Выпишем подряд все целые числа от 2 до n. Первое простое число 2. Подчеркнем его, а все большие числа, кратные 2, зачеркнем. Первое из оставшихся чисел 3. Подчеркнем его, а все большие числа, кратные 2, зачеркнем. Первое из оставшихся чисел 3, зачеркнем. Первое число из оставшихся теперь 5, так как 4 уже зачеркнуто. Подчеркнем его как простое, а все большие числа, кратные 5, зачеркнем и т.д.:
2,
3,
4,
5,
6,
7,
8,
9,
10,...
558 Дано натуральное число n. С помощью решета Эратосфена (см. предыдущую задачу) найти четверки меньших n простых чисел, принадлежащих одному десятку (например, 11, 13, 17, 19).
559 Дано натуральное число n. Найти все меньшие n числа Мерсена. (Простое число называется числом Мерсена, если оно может быть представлено в виде 2p-1, где р - тоже простое число.)
560 Два натуральных числа называют дружественными, если каждое из них равно сумме всех делителей другого, кроме самого этого числа. Найти все пары дружественных чисел, лежащих в диапазоне от 200 до 300.
561 Дано натуральное число n. Среди чисел 1, ..., n найти все такие, запись которых совпадает с последними цифрами записи их квадрата (как, например, 62 = 36, 252 = 625 и т.д.).
562 Натуральное число из n цифр является числом Армстронга, если сумма его цифр, возведенных в n-ю степень, равна самому числу (как, например, 153 = 13 + 53 + 33). Получить все числа Армстронга, состоящие из двух, трех и четырех цифр.
563 Назовем натуральное число палиндромом, если его запись читается одинаково с начала и с конца (как, например, 4884, 393, 1).
564 Рассмотрим некоторое натуральное число n. Если это не палиндром, то изменим порядок его цифр на обратный и сложим исходное число с получившимся. Если сумма не палиндром, то над ней повторяется то же действие и т, д., пока не получится палиндром. До настоящего времени неизвестно, завершается ли этот процесс для любого натурального n.
565 Рассмотрим некоторое натуральное число n (n > 1). Если оно четно, то разделим его на 2, иначе умножим на 3 и прибавим 1. Если полученное число не равно 1, то повторяется то же действие и т. д., пока не получится 1. До настоящего времени неизвестно, завершается ли этот процесс для любого n>1.
566 Найти все простые несократимые дроби, заключенные между 0 и 1, знаменатели которых не превышают 7 (дробь задается двумя натуральными числами-числителем и знаменателем).
567 Дано натуральное число n. Выяснить, можно ли представить n! в виде произведения трех последовательных целых чисел.
568 Дано натуральное число m. Вставить между некоторыми цифрами 1, 2, 3, 4, 5, 6, 7, 8, 9 записанные именно в таком порядке, знаки + , -, так чтобы значением получившегося выражения было число m. Например, если m = 122, то подойдет следующая расстановка знаков: 12 + 34 - 5 - 6 + 78 + 9. Если требуемая расстановка знаков невозможна, то сообщить об этом.
569 Дано натуральное число n. Получить в порядке возрастания n первых натуральных чисел, которые не делятся ни на какие простые числа, кроме 2, 3 и 5.
570 Алгоритм Евклида (см. задачу 89) допускает многочисленные обобщения. Например, вместе с НОД(f, g) можно вычислять целые u и v такие, что fu + gv = НОД(f, g). Это дает возможность находить некоторое целочисленное решение уравнения вида kx + ly = m, где k, l, m-целые числа такие, что k и l, m одновременно не равны 0, а m делится на d = НОД(|k|, | l |). Пусть |k|u + | l | u = d; тогда |k| um/d + | l | vm/d = m и, как следствие этого, k (c1um/d) + l (c2vm/d) = m, где cj± 1 (j = 1, 2). Укажем алгоритм нахождения целых чисел u и v, удовлетворяющих fu + gu = НОД(f, g). Обозначим временно f через f0, и g через f1. Получаемые в процессе применения алгоритма Евклида ненулевые остатки обозначим через f2, ..., fn, частные от деления f0, на f1, f1 на f2, ..., fn-1 на fn - через а1, ...., аn:
f0 = a1f 1 + f2,
f1 = a2f2 + f3,
. . . . . . . . . . . .
fn-2 = an-1fn-1 + fn,
fn-1 = anfn,
здесь НОД(f0, f1) = fn. Пусть для некоторого i ≤ n-2 вместе с числами fi, fi + 1 известны соответствующие им множители р, q, s, t такие, что f0p + f1g = fi, f0s + f1t = fi + 1. Тогда, разделив fi на fi + 1 и получив частное ai + 1 и остаток fi + 2, мы можем вычислить множители, соответствующие fi + 2: так как fi - ai + 1fi + 1 = fi + 2, то f0(p-ai + 1s) + f1(g-ai + 1t) = fi + 2.Таким образом, для нахождения целых u и v таких, что fu + gv = НОД(f g), надо применять к f и g алгоритм Евклида, рассматривая на каждом шаге его применения, кроме тех двух чисел, которые рассматривались и прежде, еще и соответствующие этим числам множители р, q и s, t. На первом шаге в качестве множителей, соответствующих исходным числам f u g, берутся 1, 0 и 0, 1. Выполнив деление и получив частное а и некоторый остаток, надо, если остаток не равен 0, вычислить по формулам р - as, q - at множители, соответствующие полученному остатку. Множители, соответствующие последнему ненулевому остатку, дадут решение рассматриваемого уравнения fu + gu = НОД(f, g).
571 Показать, что если x1, y1 и x2, y2 - два целочисленных решения уравнения kx + ly = m, то x1- x2, y1- y2- целочисленное решение уравнения kx + ly = 0. Вывести отсюда, что если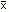 ,
, 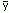 - какое-нибудь целочисленное решение уравнения kx +
ly = m, то все целочисленные решения этого уравнения описываются формулами x =
- какое-нибудь целочисленное решение уравнения kx +
ly = m, то все целочисленные решения этого уравнения описываются формулами x = 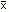 +
l't, y =
+
l't, y = 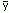 - k't, где k' = k/НОД(k, l), l` = l/НОД(k, l)
(t = 0, ±1, ±2, ...). Написать программу, которая позволяет проверить, обладает ли уравнение kx + ly = m
решением в целых неотрицательных числах, и если обладает, то позволяет построить какое-то одно такое решение.
- k't, где k' = k/НОД(k, l), l` = l/НОД(k, l)
(t = 0, ±1, ±2, ...). Написать программу, которая позволяет проверить, обладает ли уравнение kx + ly = m
решением в целых неотрицательных числах, и если обладает, то позволяет построить какое-то одно такое решение.
572 Даны натуральное число k, одновременно не равные 0 целые числа n1, ..., nk. Найти НОД (|n1|, |, ..., |nk|) и целые u1, ..., uk такие, что u1n1 + ... + uknk = НОД(|n1|, ... , |nk|) (см. задачу 333).
573 Даны натуральные взаимно простые числа n, р. Используя алгоритм, описанный в задаче 570а, найти нaтуральное m такое, что, во-первых, m < р и, во-вторых nm при делении на р дает остаток 1.
574 Известная в теории чисел китайская теорема об остатках утверждает следующее. Пусть р1, ..., рr-попарно взаимно простые натуральные числа; пусть v = p1, ... pr. Пусть а1, ..., ar-такие целые неотрицательные числа, что a1 < P1, ..., ar pr. Тогда существует ровно одно целое неотрицательное u < v, которое при делении на p1 дает остаток a1, при делении на р2 дает остаток a2, ..., при делении на рr дает остаток аr. (Процесс восстановления числа по его остаткам был известен в Китае уже около 2000 лет назад, поэтому теорема и имеет такое название). Если даны p1, ..., pr, ar, ..., аr, то на основании этой теоремы число u может быть найдено последовательной проверкой чисел 0, 1, ..., v-1. Однако есть алгоритм значительно более быстрого решения этой задачи, который мы сформулируем без доказательства (имеет смысл попытаться самостоятельно найти доказательство).
575 Цепной дробью (конечной) называется выражение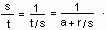
576 Даны натуральные числа a1, .... а10. Предположим, что имеются 10 гирь весом a1, ..., a10. Обозначим через сk число способов, которыми можно составить вес k, т. е. сk- это число решений уравнения a1x1 + ... + a10x10 = k, где хi, может принимать значение 0 или 1 ( i = 1, .., 10). Получить С0, ..., С10.
577 Даны натуральные числа а1, ..., a10. Предположим, что имеются 10 видов монет достоинством а1, ...., a10. Обозначим через bk число способов, которыми можно вы-платить сумму k, т. е. bk-это число решений уравнения a1x1 + ... + a10x10 = k, где xi, может принимать целые неотрицательные значения. Получить b0, ..., b.
578 Дано натуральное число n. Как наименьшим количеством монет можно выплатить n копеек? Предполагается, что в достаточно большом количестве имеются монеты достоинством в 1, 2, 3, 5, 10, 15, 20 и 50 коп.
579 Дано натуральное число n (r ≥ 5). Получить все пятерки натуральных чисел х1, x2, x3, x4, x5 такие, что х1 ≥ x2 ≥ x3 ≥ x4 ≥ x5 и x1 + ... + x5 = n.
580 Дано натуральное число n (n ≤ 99). Получить все способы выплаты суммы n с помощью монет достоинством 1, 5, 10 и 20 коп.
555 Треугольником Паскаля называется числовой треугольник
1
1 1
1 2 1
1 3 3 1
1 4 6 4 1
.......................................
в котором по краям стоят единицы, а каждое число внутри равно сумме двух стоящих над ним в ближайшей строке сверху. Дано натуральное n. Получить первые n строк треугольника Паскаля.
556 Для чисел Фибоначчи u0, u1, ...(см.задачу 144) справедлива формула Бине
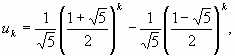 k = 0, 1, ...
k = 0, 1, ...Так как
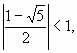 то для больших k выполнено приближенное равенство
то для больших k выполнено приближенное равенство
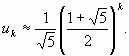
Вычислить и округлить до целого все члены
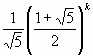 (k = 0, 1, ..., 15). Вычислить u0, u1,
..., u15 по формулам u0 = 0; u1 = 1; uk = uk-1 +
uk-2 (k = 2, 3...) и сравнить результаты.
(k = 0, 1, ..., 15). Вычислить u0, u1,
..., u15 по формулам u0 = 0; u1 = 1; uk = uk-1 +
uk-2 (k = 2, 3...) и сравнить результаты.557 Дано натуральное число n (n ≥ 2). Найти все меньшие n простые числа, используя решето Эратосфена. Решетом Эратосфена называется следующий способ. Выпишем подряд все целые числа от 2 до n. Первое простое число 2. Подчеркнем его, а все большие числа, кратные 2, зачеркнем. Первое из оставшихся чисел 3. Подчеркнем его, а все большие числа, кратные 2, зачеркнем. Первое из оставшихся чисел 3, зачеркнем. Первое число из оставшихся теперь 5, так как 4 уже зачеркнуто. Подчеркнем его как простое, а все большие числа, кратные 5, зачеркнем и т.д.:
558 Дано натуральное число n. С помощью решета Эратосфена (см. предыдущую задачу) найти четверки меньших n простых чисел, принадлежащих одному десятку (например, 11, 13, 17, 19).
559 Дано натуральное число n. Найти все меньшие n числа Мерсена. (Простое число называется числом Мерсена, если оно может быть представлено в виде 2p-1, где р - тоже простое число.)
560 Два натуральных числа называют дружественными, если каждое из них равно сумме всех делителей другого, кроме самого этого числа. Найти все пары дружественных чисел, лежащих в диапазоне от 200 до 300.
561 Дано натуральное число n. Среди чисел 1, ..., n найти все такие, запись которых совпадает с последними цифрами записи их квадрата (как, например, 62 = 36, 252 = 625 и т.д.).
562 Натуральное число из n цифр является числом Армстронга, если сумма его цифр, возведенных в n-ю степень, равна самому числу (как, например, 153 = 13 + 53 + 33). Получить все числа Армстронга, состоящие из двух, трех и четырех цифр.
563 Назовем натуральное число палиндромом, если его запись читается одинаково с начала и с конца (как, например, 4884, 393, 1).
-
а) Найти все меньшие 100 натуральные числа, которые при возведении в квадрат дают палиндром.
б) Найти все меньшие 100 числа палиндромы, которые при возведении в квадрат также дают палиндромы.
564 Рассмотрим некоторое натуральное число n. Если это не палиндром, то изменим порядок его цифр на обратный и сложим исходное число с получившимся. Если сумма не палиндром, то над ней повторяется то же действие и т, д., пока не получится палиндром. До настоящего времени неизвестно, завершается ли этот процесс для любого натурального n.
- Даны натуральные числа k, l, m (k ≤ l). Проверить, верно ли, что
для любого натурального числа из диапазона от k до l процесс завершается не позднее, чем после таких
действий.
565 Рассмотрим некоторое натуральное число n (n > 1). Если оно четно, то разделим его на 2, иначе умножим на 3 и прибавим 1. Если полученное число не равно 1, то повторяется то же действие и т. д., пока не получится 1. До настоящего времени неизвестно, завершается ли этот процесс для любого n>1.
- Даны
натуральные числа k, l, m (1<к ≤ l). Проверить, верно ли, что для любого натурального n из
диапазона от k до l процесс завершается не позднее, чем после m таких действий.
566 Найти все простые несократимые дроби, заключенные между 0 и 1, знаменатели которых не превышают 7 (дробь задается двумя натуральными числами-числителем и знаменателем).
567 Дано натуральное число n. Выяснить, можно ли представить n! в виде произведения трех последовательных целых чисел.
568 Дано натуральное число m. Вставить между некоторыми цифрами 1, 2, 3, 4, 5, 6, 7, 8, 9 записанные именно в таком порядке, знаки + , -, так чтобы значением получившегося выражения было число m. Например, если m = 122, то подойдет следующая расстановка знаков: 12 + 34 - 5 - 6 + 78 + 9. Если требуемая расстановка знаков невозможна, то сообщить об этом.
569 Дано натуральное число n. Получить в порядке возрастания n первых натуральных чисел, которые не делятся ни на какие простые числа, кроме 2, 3 и 5.
570 Алгоритм Евклида (см. задачу 89) допускает многочисленные обобщения. Например, вместе с НОД(f, g) можно вычислять целые u и v такие, что fu + gv = НОД(f, g). Это дает возможность находить некоторое целочисленное решение уравнения вида kx + ly = m, где k, l, m-целые числа такие, что k и l, m одновременно не равны 0, а m делится на d = НОД(|k|, | l |). Пусть |k|u + | l | u = d; тогда |k| um/d + | l | vm/d = m и, как следствие этого, k (c1um/d) + l (c2vm/d) = m, где cj± 1 (j = 1, 2). Укажем алгоритм нахождения целых чисел u и v, удовлетворяющих fu + gu = НОД(f, g). Обозначим временно f через f0, и g через f1. Получаемые в процессе применения алгоритма Евклида ненулевые остатки обозначим через f2, ..., fn, частные от деления f0, на f1, f1 на f2, ..., fn-1 на fn - через а1, ...., аn:
f0 = a1f 1 + f2,
f1 = a2f2 + f3,
. . . . . . . . . . . .
fn-2 = an-1fn-1 + fn,
fn-1 = anfn,
здесь НОД(f0, f1) = fn. Пусть для некоторого i ≤ n-2 вместе с числами fi, fi + 1 известны соответствующие им множители р, q, s, t такие, что f0p + f1g = fi, f0s + f1t = fi + 1. Тогда, разделив fi на fi + 1 и получив частное ai + 1 и остаток fi + 2, мы можем вычислить множители, соответствующие fi + 2: так как fi - ai + 1fi + 1 = fi + 2, то f0(p-ai + 1s) + f1(g-ai + 1t) = fi + 2.Таким образом, для нахождения целых u и v таких, что fu + gv = НОД(f g), надо применять к f и g алгоритм Евклида, рассматривая на каждом шаге его применения, кроме тех двух чисел, которые рассматривались и прежде, еще и соответствующие этим числам множители р, q и s, t. На первом шаге в качестве множителей, соответствующих исходным числам f u g, берутся 1, 0 и 0, 1. Выполнив деление и получив частное а и некоторый остаток, надо, если остаток не равен 0, вычислить по формулам р - as, q - at множители, соответствующие полученному остатку. Множители, соответствующие последнему ненулевому остатку, дадут решение рассматриваемого уравнения fu + gu = НОД(f, g).
-
а) Даны одновременно не равные 0 целые f u g. Найти НОД(|f|, |g|) и целые u, v такие , что fu + gv =
НОД(|f|, |g|).
б) Даны целые k, l, m такие, что k и l одновременно не равны 0, а m делится на НОД(|k|, |l|). Найти какое-нибудь целочисленное решение уравнения kx + ly = m.
в) Заметим, что предложенный выше алгоритм поиска множителей u и v можно изменить так, что число требуемых им операций сократится почти в полтора раза: из двух чисел u и v достаточно вычислить вместо НОД (f, g) только v, а затем определить u по формуле u = (НОД(f, g)-gv)/f. Внести это усовершенствование в программы, дающие решения заданий а), б).
571 Показать, что если x1, y1 и x2, y2 - два целочисленных решения уравнения kx + ly = m, то x1- x2, y1- y2- целочисленное решение уравнения kx + ly = 0. Вывести отсюда, что если
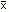 ,
, 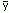 - какое-нибудь целочисленное решение уравнения kx +
ly = m, то все целочисленные решения этого уравнения описываются формулами x =
- какое-нибудь целочисленное решение уравнения kx +
ly = m, то все целочисленные решения этого уравнения описываются формулами x = 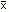 +
l't, y =
+
l't, y = 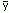 - k't, где k' = k/НОД(k, l), l` = l/НОД(k, l)
(t = 0, ±1, ±2, ...). Написать программу, которая позволяет проверить, обладает ли уравнение kx + ly = m
решением в целых неотрицательных числах, и если обладает, то позволяет построить какое-то одно такое решение.
- k't, где k' = k/НОД(k, l), l` = l/НОД(k, l)
(t = 0, ±1, ±2, ...). Написать программу, которая позволяет проверить, обладает ли уравнение kx + ly = m
решением в целых неотрицательных числах, и если обладает, то позволяет построить какое-то одно такое решение.572 Даны натуральное число k, одновременно не равные 0 целые числа n1, ..., nk. Найти НОД (|n1|, |, ..., |nk|) и целые u1, ..., uk такие, что u1n1 + ... + uknk = НОД(|n1|, ... , |nk|) (см. задачу 333).
573 Даны натуральные взаимно простые числа n, р. Используя алгоритм, описанный в задаче 570а, найти нaтуральное m такое, что, во-первых, m < р и, во-вторых nm при делении на р дает остаток 1.
574 Известная в теории чисел китайская теорема об остатках утверждает следующее. Пусть р1, ..., рr-попарно взаимно простые натуральные числа; пусть v = p1, ... pr. Пусть а1, ..., ar-такие целые неотрицательные числа, что a1 < P1, ..., ar pr. Тогда существует ровно одно целое неотрицательное u < v, которое при делении на p1 дает остаток a1, при делении на р2 дает остаток a2, ..., при делении на рr дает остаток аr. (Процесс восстановления числа по его остаткам был известен в Китае уже около 2000 лет назад, поэтому теорема и имеет такое название). Если даны p1, ..., pr, ar, ..., аr, то на основании этой теоремы число u может быть найдено последовательной проверкой чисел 0, 1, ..., v-1. Однако есть алгоритм значительно более быстрого решения этой задачи, который мы сформулируем без доказательства (имеет смысл попытаться самостоятельно найти доказательство).
- Обозначим через vi(1 ≤ i ≤ r) произведение всех
р1, ..., рr, кроме pi, т. е. vi = p1...pi-1p
i + 1...pr = v/pi. Пусть числа wi (1 ≤ i ≤ r) таковы, что
1 ≤ wi < рi и viwi при делении на pi дает остаток 1
(см. предыдущую задачу). Тогда можно положить u равным остатку от деления v1w1a1
+ ... + vrwrar на v. Например, если р1, р2, р3,
p4 равно соответственно 2, 3, 5, 7, а a1, a
- Даны натуральные числа r, р1, ...,
pr целые неотрицательные числа ai, ..., ar, (p1, ..., рr, -
попарно взаимно простые, а1 < р1, ..., аr < рr). Найти u,
удовлетворяющие сформулированным выше условиям.
575 Цепной дробью (конечной) называется выражение
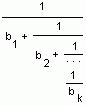
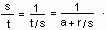
- Полагаем b1 = а, затем этим же способом преобразуем r/s и получаем b1 и т. д. Видно,
что b1, ..., bk-это последовательность частных, возникающих в процессе применения к s и t
алгоритма Евклида (см. задачу 89). Итак, пусть s/t = [b1, ...,
bk]. Дополнительно рассмотрим цепные дроби [b1][b1, b2], ...,
[b1, ..., bk-1], значения которых называются подходящими Дробями числа s/t. Обозначим
несократимые формы подходящих дробей через p1/g1, ..., рk-1/gk-1.
Подходящие дроби обладают следующими важными свойствами:
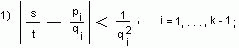
2) если для некоторой дроби u/v и подходящей дроби pi/qi (1 ≤ i < k-1) выполнено
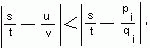
то v > gi
- Свойства 1), 2) используются в
решении разнообразных практических задач, требующих подбора для данного рационального числа хорошего приближения
в виде дроби со сравнительно небольшим знаменателем. Примером может служить задача расчета зубчатой передачи,
состоящей из двух шестерен. Передаточное число должно быть близко к заданному значению, и при этом число зубьев
каждой из шестерен не может превышать некоторой указанной границы. Для решения такого рода задач полезны следующие
соотношения для числителей и знаменателей подходящих дробей: p1 = 1; p2 = b2;
pn = bnpn-1 + pn-1, n = 3, 4, ..., k-1; g1 = b1;
g2 = b1b2 + 1; gn = bngn-1 + gn-2,
n = 3, 4, ..., k-1.
-
Написать программы выполнения следующих заданий. Даны натуральные s, t (s < t).
-
а) Получить все подходящие дроби числа s/t (указать их числители и знаменатели).
б) Считая, что дополнительно дано натуральное k, выяснить, существуют ли такие подходящие дроби числа s/t, числители и знаменатели которых меньше k. Если такие подходящие дроби существуют, то построить последнюю по порядку (указать ее числитель и знаменатель), а также указать модуль разности числа r/s и найденной подходящей дроби.
576 Даны натуральные числа a1, .... а10. Предположим, что имеются 10 гирь весом a1, ..., a10. Обозначим через сk число способов, которыми можно составить вес k, т. е. сk- это число решений уравнения a1x1 + ... + a10x10 = k, где хi, может принимать значение 0 или 1 ( i = 1, .., 10). Получить С0, ..., С10.
577 Даны натуральные числа а1, ..., a10. Предположим, что имеются 10 видов монет достоинством а1, ...., a10. Обозначим через bk число способов, которыми можно вы-платить сумму k, т. е. bk-это число решений уравнения a1x1 + ... + a10x10 = k, где xi, может принимать целые неотрицательные значения. Получить b0, ..., b
578 Дано натуральное число n. Как наименьшим количеством монет можно выплатить n копеек? Предполагается, что в достаточно большом количестве имеются монеты достоинством в 1, 2, 3, 5, 10, 15, 20 и 50 коп.
579 Дано натуральное число n (r ≥ 5). Получить все пятерки натуральных чисел х1, x2, x3, x4, x5 такие, что х1 ≥ x2 ≥ x3 ≥ x4 ≥ x5 и x1 + ... + x5 = n.
580 Дано натуральное число n (n ≤ 99). Получить все способы выплаты суммы n с помощью монет достоинством 1, 5, 10 и 20 коп.
 Предыдущая глава
Предыдущая глава