§36 Некоторые примеры программирования

1047 При программировании практических задач часто приходится работать с различными списками. Ппимерами могут служить список учеников 9а класса, список учителейлей, преподающих литературу во всех 10-х классах школы, список участников спортивной игры и т. п. Каждый элемент списка содержит, как правило, несколько полей. Например, элементы списка выпускников школы могут включать имя и фамилию ученика, а также его средний балл по аттестату.
Представление списков в памяти ЭВМ может быть основано на последовательном и на связанном распределении памяти. При последовательном распределении элементы списка (будем также называть их узлами) размещаются последовательно, один за другим. При связанном распределении памяти местоположение каждого элемента заранее неизвестно - блок памяти, который отводится для размещения отдельного элемента, выделяется из одной большей области памяти по специальным алгоритмам (см. задачу 1052). 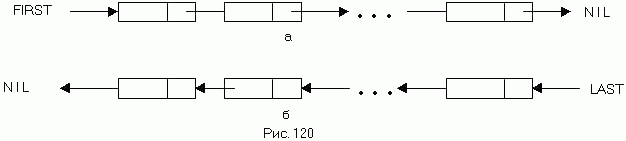Поэтому все узлы содержат по крайней мере одно дополнительное поле - поле связи со следующим (рис. 120, а) или предыдущим узлом (рис. 120,6) (см. также задачи 531, 532). На рис. 120 FIRST - это переменная, указывающая на первый узел в списке; LAST - переменная, указывающая на последний узел в списке; стрелки обозначаютсвязи между узлами; NIL - значение поля связи, говорящее о том, что данный узел не связан ни с каким другим узлом (является последним ца рис. 120, а и первым на рис. 120,6).



Связанное распределение памяти обеспечивает существенно более высокую гибкость при работе со списками, чем последовательное распределение, значительно упрощая включение нового узла в список и исключение из него.
Наиболее часто используются следующие виды связанного распределения памяти (далее, под термином список мы будем понимать конкретное представление соответствующей информационной структуры в памяти ЭВМ на основе связанного распределения памяти):

1) Односвязные списки, в которых каждый элемент содержит поле связи либо со следующим, либо с предыдущим элементом списка (рис. 120).
2) Односвязные циклические списки, в которых последний элемент содержит поле связи с первым элементом (рис. 121) (см. задачу 545).



3) Двусвязные списки, в которых каждый элемент содержит поле связи со следующим элементом и с предыдущим (рис. 122) (см. задачу 533).



При работе с линейными списками требуется, как правило, выполнять следующие операции [34]:


1) Получить доступ к k - му узлу списка, чтобы проанализировать и/или изменить содержимое его полей.
2) Включить новый узел непосредственно перед k - м узлом.
3) Исключить k - й узел.
4) Объединить два (или более) списка в один список.
5) Разбить список на два (или более) списка.
6) Сделать копию списка.
7) Определить число узлов в списке.
8) Выполнить сортировку узлов списка по значениям некоторых полей.
9) Найти в списке узел с заданным значением некоторого поля.


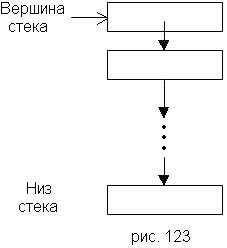
Составить процедуры, реализующие перечисленные выше операции 1)-9) для работы с односвязными, односвязными циклическими и двусвязными списками.

1048 Одним из наиболее часто встречающихся видов списка является стек-список, в котором все включения и исключения элементов делаются только на одном его конце - вершине стека (рис. 123). Механизм функционирования стека хорошо отражен в другом его названии- список типа "LIFO" (last in first out- "последним вошел - первым вышел"). При работе со стеком предполагаются две операции: занесение очередного элемента в вершину стека и удаление элемента, находящегося в вершине стека. Тем самым операция удаления элемента из стека может быть применена только к элементу, помещенному в стек самым последним. И, следовательно, любой элемент не может быть удален из стека раньше, чем будут удалены все элементы, помещенные в стек после него.



Составить процедуры, реализующие операции занесения элемента в стек и удаления элемента из его вершины.



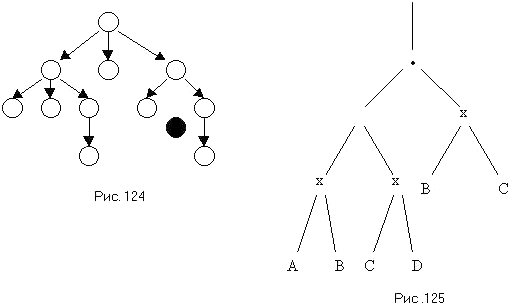
1049 Еще один из наиболее важных видов структур, встречающихся в программировании, представляют собой деревья. Формально дерево (рис. 124) определяется как конечное множество T, состоящее из одного или более узлов таких, что

1) имеется один узел, называемый корнем дерева;
2) остальные узлы (исключая корень) содержатся в m > 0 попарно непересекающихся множествах T₁, .... T_m, каждое из которых в свою очередь является деревом;

деревья T₁, .... T_m называются поддеревьями данного корня [34]. Деревья, как правило, дают хорошее представление о структурных отношениях между элементами данных. Так, например, на рис. 125 показано дерево, представляющее формулу (АВ + CD)/BC. Здесь ветвь, отходящая от вершины / влево, представляет числитель дроби, а ветвь, отходящая вправо,- ее знаменатель и т. д.



Еще один пример - фрагмент дерева (рис. 126), показывающего возможные ходы при игре в восемь (эта игра аналогична игре в пятнадцать); исходная и целевая позиции приведены соответственно на рис. 127, и и 127,6 [41]. Далее мы будем рассматривать только бинарные деревья. Бинарное дерево определяется как конечное множество узлов, которое либо пусто, либо состоит из корня и двух бинарных деревьев (рис. 128). При рзаботе с древовидными структурами наиболее часто приходится решать задачу обхода дерева - такого последовательного прохождения по узлам дерева, когда каждый узел встречается ровно один раз. Для обхода бинарного дерева можно воспользоваться одним из трех способов: можно проходить узлы в префиксном порядке, в инфиксном порядке и в суффиксном порядке.



Префиксный порядок обхода дерева определяется в виде списка проходимых узлов следующим образом. Если дерево не пусто, префиксный порядок - это корень дерева; узлы левого поддерева в префиксном порядке; узлы правого поддерева в префиксном порядке. Инфиксный порядок обхода дерева определяется следующим образом. Если дерево пусто, список узлов пуст. Если дерево не пусто, инфиксивный порядок - это узлы левого поддерева в инфиксном порядке; корень дерева; узлы правого поддерева в инфиксном порядке. Суффиксный порядок обхода дерева определяется следующим образом. Если дерево пусто, список узлов пуст. Если дерево не пусто, суффиксный порядок - это узлы левого поддерева в суффиксном порядке;узлы правого поддерева в суффиксном порядке;корень дерева. Составить процедуры обхода заданного бинарного дерева в префиксном, инфиксном и суффиксном порядке.

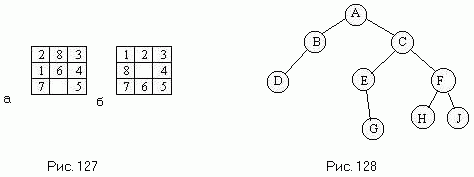
1050 Составить процедуру подсчета числа узлов заданного бинарного дерева.

1051 Листом дерева называется вершина, не являющаяся корнем никакого поддерева. Составить процедуру подсчета числа листьев заданного бинарного дерева.

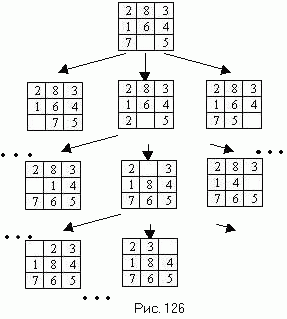
1052 Алгоритмами динамического распределения памяти называют алгоритмы, позволяющие выделять и освобождать различные по размеру блоки памяти, беря их из одной большой области памяти. (Здесь и далее используются термины блок и область, обозначающие совокупность смежных ячеек памяти.)


Будем считать, что вся имеющаяся свободная память представлена в виде списка свободных блоков. В начальный момент в списке только один блок, содержащий всю свободную память. Каждый блок содержит заголовок с размерами блока и указателем на следующий блок. Выделение свободной памяти по запросу часто выполняется либо по методу "наиболее подходящего", либо по методу "первого подходящего".

Метод "наиболее подходящего" заключается в том, что среди всех блоков, имеющих размер, не меньший требуемого, выбирается блок с наименьшим размером. Метод "первого подходящего" заключается в том, что выделению подлежит первый в порядке просмотра элементов списка блок, размер которого не меньше требуемого.

Если блок, выбранный по одному из двух указанных методов, имеет размер, превышающий указанный при запросе, он расщепляется на два: первый блок имеет требуемый размер и предоставляется в ответ на запрос, второй блок - остаток - остается в списке свободной памяти. При освобождении блока смежные блоки склеиваются.

Реализовать процедуру для выделения блока свободной памяти заданного размера (результатом работы процедуры должна быть -1, если блок такого размера выделен быть не может) и процедуру для освобождения - повторного включения в список свободной памяти блока, выделенного ранее.

Предыдущая глава

К началу