843 Построить графики *) линейной функции y = kx для
k = 0.1, 0.2, 0.3, ..., 1.
844 Построить графики функций:
845 Построить графики функций, указанных в задаче 337.
846 Исследовать область определения и построить графики следующих функций:
847 Построить кривые по заданному параметрическому представлению **).
844 Построить графики функций:
-
а) y = 3x2;
б) y = -6x2 + 3x;
в) y = x3 + 2x2 + x;
г) y = x5;
д) y = sin x;
е) y = cos(x-1) + |x|;
845 Построить графики функций, указанных в задаче 337.
846 Исследовать область определения и построить графики следующих функций:
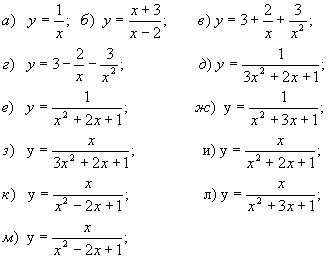
-
а) Окружность радиуса r с центром в начале координат; x = r cos t, y = r sin t,
t Є [ 0, 2π ).
б) Эллипс с большой и малой полуосями, равными соответственно r1 и r2 и расположенными параллельно осям координат: x = r1 cos t, y = r2 sin t, t Є [ 0, 2π )
в) Улитка Паскаля (рис. 58): x = a cos 2 t + b cos t, y = a cos t sin t + b sin t, a > 0, b > 0, t Є [ 0, 2π ).Рассмотреть случаи, когда b ≥ 2a, a < b < 2a, a > b.
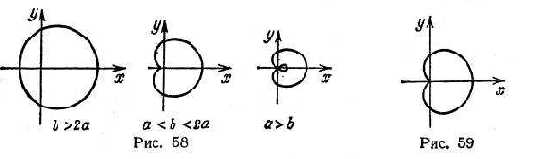
г) Кардиоида (рис. 59): x = a cos t(1+cost), y = a sin t(1+cost), a>0, t Є [ 0, 2π )..
д) Эпициклоида (рис. 60): x = (a+b)cost-acos((a+b)t/a), y = (a+b)sint-asin((a+b)t/a), a>0, b>0. Рассмотреть следующие случаи:
-
1) если b/a есть целое положительное число, t Є [ 0, 2π );
2) если b/a = p/q, где p и q - положительные целые взаимно простые числа, t Є [ 0, 2qπ )
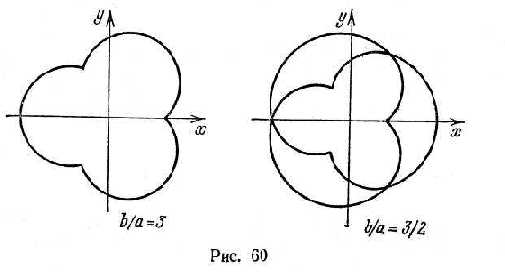
е) Астроида (рис. 61): x = b cos3 t, y = b sin3t, t Є [ 0, 2π ).
ж) Циссоида (рис. 62): x = at2/(1 + t2), y = at3/(1 + t2), t Є ( -∞, ∞), a > 0.
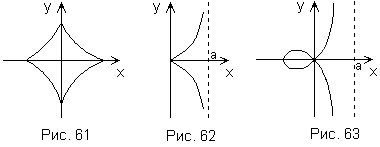
з) Строфоида (рис. 63): x = a(t2 - 1)/(t2 + 1), y = at(t2 - 1)/(t2 + 1), t Є (-∞, ∞), a > 0.
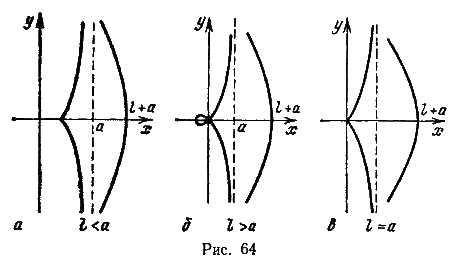
и) Конхоида Никомеда (рис. 64): x = a + lcos t, y = a tg t + lsin t, t Є (-π/2, π/2) - правая ветвь, t Є (π/2, 3π/2) - левая ветвь, a > 0, l > 0. Рассмотреть случаи, когда l > a, l < a, l = a.
849 Рассмотрим треугольник ос сторонами x, x + 1, x + 2, где x - некоторое действительное число (рис. 67). Угол α между сторонами x и x + 1 является функцией от x. Исследовать область определения и построить график этой функции.
850 Вычерчивание окружности, заданной параметрическими уравнениями x = rcost, у - r sin t, t Є [ 0, 2π ) (см. предыдущую задачу), выполняется довольно медленно в связи с необходимостью вычисления тригонометрических функций. Процесс можно ускорить, если воспользоваться параметрическими уравнениями
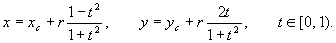
Указанное изменение параметра соответствует дуге окружности от 0 до π/2. Полная окружность может быть построена симметричным отображением каждой полученной точки относительно оси ОХ, оси OY и начала координат в предположении, что начало координат совмещено с центром окружности (рис. 69). Даны натуральные xc, yc,r. Построить окружность с центром в точке xc, yc и радиусом r, воспользовавшись алгоритмом, описанным выше.
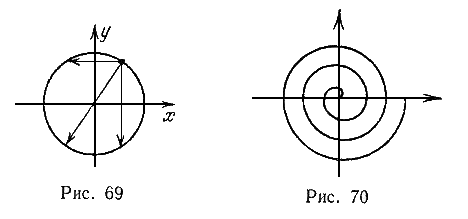
851 Построить спираль вокруг начала координат с n витками и внешним радиусом r, начальное направление спирали образует с осью ОХ угол α (рис. 70). Параметрическое представление спирали: x = r cos t, y = r sin t, r = t/2, α ≤ t ≤ 2nπ.
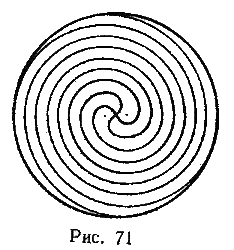
852 Используя решение предыдущей задачи, начертить фигуру, показанную на рис. 71. Фигура состоит из четырех спиралей, заключенных в окружность радиуса r с центром в точке (xc, yc). На чальный угол одной из спиралей задан и равен α, начальный угол каждой следующей спирали превышает начальный угол каждой предыдущей спирали на 45°.
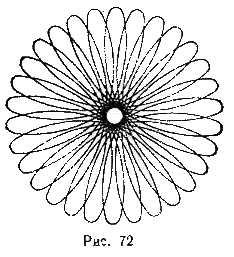
853 Спирограф - это зубчатый диск радиуса В, расположенный внутри колеса радиуса А. Диск вращается против часовой стрелки и всегда находится в зацеплении с внешним колесом. В диске имеется небольшое отверстие на расстоянии D от центра диска, в которое помещается карандаш. Грифель карандаша в процессе вращения вычерчивает рисунок; вычерчивание заканчивается, когда карандаш возвращается в исходное положение. С помощью спирографа могут быть построены рисунки, подобные приbеденному на рис. 72. Уравнение кривой, вычерчиваемой грифелем, в параметрической форме имеет вид
-
х = (А - В) cos t - D cos φ
y = (A - B) sin t - D sin φ, где φ = (A/B)t, D < B < A.
- Даны натуралыше А, В, D (D < В < А). Составить программу, моделирующую спирограф.
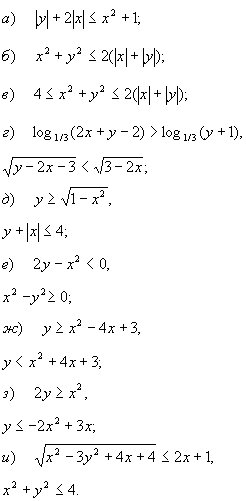
855 Кривые дракона, показанные на рис. 73, а-73, в, могут быть построены с
помощью следующего рекуррентного метода. Каждой кривой ставится в соответствие последовательность,
состоящая из нулей и единиц (будем называть ее двоичной формулой), где единица соответствует повороту
кривой налево, а нуль-повороту направо. Кривая дракона первого порядка имеет двоичную формулу 1
(рис. 73, а). Для того чтобы получить двоичную формулу кривой дракона каждого следующего порядка,
следует приписать справа к формуле кривой предыдущего порядка единицу. Полученная последовательность
дает половину искомой формулы. Затем в последовательности цифр, предшествующих приписанной единице,
следует заменить на нуль единицу, стоящую в ее середине, после чего приписать полученную последовательность
справа от уже построенной части формулы. На рис. 73, б показана кривая дракона второго порядка, которой
соответствует двоичная формула ПО, а на рис. 73, в-кривая дракона третьего порядка-ей соответствует
двоичная формула 1101100. Кривые строятся от хвоста к голове дракона и повернуты так, чтобы драконы
"плыли" направо, а пасть и кончик хвоста касались "поверхности воды". Прямые углы обычно скругляются
дугой окружности или срезаются (показано на рис. 73, а-73, в штриховой линией) для того, чтобы вершины
углов не соприкасались и не создавалась иллюзия самопересечения кривой.
857 Даны натуральные числа n и r. Построить n точек, являющихся вершинами правильного n - угольника, вписанного в окружность радиуса r, и соединить каждую из точек со всеми остальными n-1 точками. Координаты точек задаются формулами xi = r cos(2πi/n), yi = r sin(2πi/n) (i = 1, 2, ..., n). Во избежании повторного вычерчивания линий, соединяющих одни и те же точки, каждую точку с номером i следует соединять толко с теми точками с номерами j для которых выполнено условие i < j.
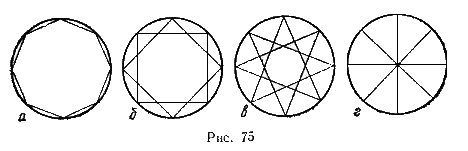
858 Дано натуральное число r. Построить фигуры, показанные на рис. 75, а - 75, г. Фигуры образованы окружность радиуса r и восемью точками, являющимися вершинами правильного многоугольника, вписанного в эту окружность, и соединенных между собой определенным образом. Фигура на рис. 75, а - это правильный восьмиугольник, образованный последовательным соединением его вершин. Для построения фигуры на рис. 75, б следует соединять вершины многоугольника через одну. При построении фигуры на рис. 75, в соединяются вершины, отстоящие друг от друга на две вершины, а при построении фигуры на рис. 75, г-отстоящие на три вершины.
859 Даны натуральные числа n и r. Построить квадрат, длина стороны которого равна r. Разместить по одной точке в каждом углу квадрата и по n-1 точек на каждой его стороне. Расстояния между соседними точками на любой из сторон должны быть одинаковыми и равными r/n. Тем самым будет построено всего 4n точек, которые можно занумеровать числами 1, ..., 4n (нумерация начинается с левого верхнего угла квадрата и выполняется последовательно). Соединить каждую точку с номером i со всеми точками с номерами j (i,j = 1,..., 4n) такими, что j > i и разность j-i есть число Фибоначчи, меньшее 4n (см. задачу 144).
860 Уравнение f(х, у) = 0, представляющее все точки (х, у) некоторой кривой, называют уравнением кривой в неявной форме. Если кривая делит плоскость на две части, то уравнение в неявной форме позволяет определить, лежит ли точка на кривой, или если нет, то в какой части она лежит (см. задачу 52).
861 Даны натуральные числа а, b, с, n,a0, ..., a2n-1. Числа а, b, с задают прямую l с уравнением ax + by + с = 0. Пары чисел ai, ai+1 (i кратно 2) являются коордннатами точек.
863 Пусть дана система линейных неравенств
864 Пусть две точки заданы своими координатами (x1, y1) и (x2, y2). Прямая, проходящая через эти две точки, может быть описана следующими параметрическими уравнениями:
865 Начертить узор, показанный на рис. 76. Узор образован 20 вложенными квадратами. Стороны первого квадрата параллельны осям координат экрана и равны 60. Вершины каждого последующего квадрата - это точки на сторонах предыдущего квадрата, делящие эти стороны в отношении µ = 0,08 (см. предыдущую задачу).
866 Начертить узор, повторяющий узор, описанный в предыдущей задаче, но составленный из
867 Построить узор, показанный на рис. 77, используя алгоритм, описанный в задаче 864.
868 Даны натуральные числа x1, y1,x2, y2.Начертить штриховые линии между точками (x1, y1) и (x2, y2) так, как показано на рис. 78. Способ определения координат с концами (x1, y1) и (x2, y2) и делящей отрезок в заданном отношении, см. в задаче 864.
869 Даны натуральные числа x1, y1,x2, y2,x3, y3,x4, y4. Построить две прямые, одна из которых проходит через точки с координатами (x1, y1) и (x2, y2), а другая - через точки с координатами (x3, y3) и (x4, y4). Построить точку пересечения этих прямых, если она существует, и определить, лежит ли точка пересечения внутри отрезков с концами (x1, y1), (x2, y2) и x3, y3, x4, y4 или вне их (см. задачу 864).
870 Даны целые числа t1, t2, ..., t31. Последовательность значений t1, t2, ..., t31 задает график температур за март месяц, подобный показанному на рис. 79. Построить график температур. Отрезки прямых, лежащие выше горизонтальной прямой, соответствующей нулевой температуре, и лежащие ниже зтой прямой, должны быть окрашены в разные цвета.
871 даны натуральные числа x1, y1, x2, y2, x3, y3. Построить отрезок с координатами окнцов (x1, y1) и (x2, y2), а также отрезок, параллельный и равный по длине первому отрезку; один конец отрезка должен иметь координаты(x4, y4), второй следует расположить:
872 Даны натуральные числа x1, y1,x2, y2, x3, y3. Построить отрезок с координатами концов (x1, y1) и (x2, y2). Через точку (x3, y3) провести отрезок, таким образом, чтобы точка (x3, y3) делила искомый отрезок пополам (см. предыдущую задачу и задачу 864).
873 Даны натуральные числа xc, yc,h,ω, x, y. Построить прямоугольник с центром в точке (xc, yc), высотой h и шириной ω, а также отрезок прямой с координатами концов (xc, yc) и (x,y). Отметить точку пересечения отрезка со стороной прямоугольника (рис. 80).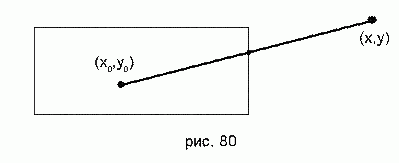
874 Даны натуральные числа xc, yc,h,ω, x, y. Построить прямоугольник с центром в точке(xc, yc), высотой h и шириной ω, а также определить координаты xp, yp точки пересеченмя невидимой прямой, проходящей через точки (xc, yc) и (x, y) (см. предыдущую задачу). Кроме того построить:
875 Прямоугольник задан координатами левого верхнего и правого нижнего угла, отрезок - координатами концов. Предполагается, что отрезок пересекает противоположные стороны прямоугольника так, как показано на рис. 82, а. Построить фигуру, изображенную на рис. 82, б (см. задачу 873).
876 Даны натуральные числа xc, yc, r, x, y. Построить окружность с центром в точке (xc, yc) и радиусом r, а также отрезок с координатами концов (xc, yc) и (x, y). Отметить точку пересечения отрезка и окружности.
877 Даны натуральные числа xc, yc, r, x, y. Построить окружность с центром в точке (xc, yc) и радиусом r, а также определить координаты xp, yp точки пересечения с окружностью невидимой прямой, проходящей через точки (xc, yc) и (x,y). Кроме того, построить отрезок с координатами концов:
878 Даны натуральные числа x1, y1, x2, y2, действительное µ(0 < µ < 1). Построить отрезок с координатами концов (x1, y1), (x2, y2) и восстановить перпендикуляр к отрезку из точки (x3, y3), делящей его в отношении µ/(1-µ).
879 Даны натуральные числа x1, y1, x2, y2, x3, y3. Построить отрезок с координатами концов (x1, y1), (x2, y2) и опустить на него или не на его продолжение перпендикуляр из точки (x3, y3) (см. предыдущую задачу и задачу 876).
880 Даны натуральные числа x1, y1, x2, y2. Построить отрезок с координатами концов (x1, y1), (x2, y2) и какой-нибудь отрезок, параллельный и равный по длине первому отрезку и отстоящему от него на 30 единиц (см. задачи 871 и 878).
881 Пусть стрелка, соединяющая две произвольные точки, устроена, как в задаче 127. Даны натуральные числа x1, y1, x2, y2. Построить стрелку, направленную из точки (x1, y1) в точку (x2, y2). (Способ определения координат точки, лежащей на отрезке с заданными концами и делящей отрезок в заданном отношении, см. в задаче 864. Способ построения прямой, перпендикулярной данной, см. в задаче 878.)
882 Даны натуральные числа x, y, r, x1, y1, h, ω. Построить окружность радиуса r с центром в точке (x, y), прямоугольник с центром в точке (x1, y1), высотой h и шириной ω, а также отрезок, соединяющий центр окружности с центром прямоугольника (рис. 83).
883 Даны натуральные числа x,y,r,x1, y1, h, ω. Построить окружность радиуса r с центром в точке (x,y), прямоугольник с центром в точке (x1, y1), высотой h и шириной ω, а также отрезок, соединяющий центр окружности с центром прямоугольника. Отрезок должен лежать на невидимой прямой с окружностью и заканчиваться в точке пересечения прямой с прямоугольником (рис. 84).
884 Даны натуральные числа x, y, n, символы S1, ..., Sn. Последовательность символов S1, ..., Sn вывести так, чтобы точка с координатами (x, y) была расположена (рис. 85):
885 Пусть в двумерной декартовой системе координат задана плоская фигура и пусть (x, y) - координаты одной из ее точек. Рассмотрим, как изменятся эти координаты, если к фигуре применить одно из следующих преобразований:перенос вдоль осей координат, поворот вокруг начала координат, растяжение (сжатие) по осям координат.
886 Даны натуральные числа xc, yc, r и действительное число t. Построить правильный пятикгольник, вписанный в окружность с центром в точке (xc, yc) радиусом r, после чего повернуть его от ординат на угол t радиан (см.предыдущую задачу).
887 Даны натуральные числа xc, yc, r, sx, sy. Построить правильный шестиугольник с центром в точке (xc, yc) и стороной r, после чего растянуть (сжать) его по оси OX в sx раз, а по оси OY - в sy раз (см. задачу 885).
888 Построить фигуру, изображенную на рис. 86. В центре фигуры находятся с заданной стороной (см. задачу 885).
889 Выполнить задания а) - е) задачи 849, после чего применить к построенным фигурам следующие преобразования:
890 Построить спираль, описанную в задаче 851, после чего применить к ней преобразования а) - в) предыдущей задачи.
891 Даны натуральные числа xc, yc, a, b и действительное t. Начертить эллипс с центром в точке (xc, yc), большой осью a, малой осью b; большая ось образует угол t радиан с положительной полуосью ОХ
(рис. 87).
892 Даны натуральные числа xc, yc, r и действительное число t. Начертить астроиду радиуса r с центром в точке (xc, yc), где одна из осей фигуры составляет угол t радиан с положительной полуосью ОХ (рис. 88). (См. задачи 849 и 885.)
893 Один из возможных способов построения на экране букв произвольного размера был описан в задаче 131. Другой достаточно широко распространенный способ заключается в том, что буквы строятся из отдельных отрезков, размещаемых в соответствии с конфигурацией буквы в прямоугольнике определенного размера, подобно тому,это делается при написании цифр на электронных часах или индекса на почтовом конверте (рис. 89). Если предположить, что левый нижний угол прямоугольника совмещен с началом координат, то каждому отрезку можно поставить в соответствие координаты его концов. Так, букве Б, изображенной на рис. 90, соответствует последовательность координат (0, 0)-(0, 8), (0, 8) - (4, 8), (0, 4)- (4,4), (0,0) - (4,0), (4,4)-(4,0)-назовем ее векторным шаблоном буквы. Таким образом, последующая обрисовка буквы на экране сводится к построению отрезков, координаты концов которых определяются согласно векторному шаблону и с учетом позиции экрана, в которую должен быть помещен левый нижний угол соответствующего прямоугольника. (Перенос и другие преобразования фигур описаны в задаче 885.)
894 Используя шаблоны, описанные в предыдущей задаче, выполнить подрисуночные подписи к графикам функций из задач 843-849.
895 Даны натуральные числа x1, y1x2, y2x3, y3x4, y4. Построить прямоугольник, левый верхний угол которого находится в точке (x1, y1), а правый нижний - в точке (x2, y2), и прямоугольник, левый верхний угол которого находится в точке (x3, y3)" а правый нижний - в точке (x4, y4). Определить, пересекаются ли эти прямоугольники. Если да, то закрасить их общую часть.
Для решения задачи воспользовался следующим. Пусть
896 Два прямоугольника заданы координатами своих левого верхнего и правого нижнего углов. Верно ли что прямоугольники пересекаются и что первый из них расположен левее и ниже, чем второй? Если да, то построить фигуру, показанную на рис, 92 (см. предыдущую задачу).
897 Вопрос о том, пересекаются ли две (или более) плоские геометрические фигуры, отчасти может быть сведен к более простому вопросу о том, пересекаются ли прямоугольники, объемлющие эти фигуры. В случае, когда прямоугольники не пересекаются, не пересекаются и сами фигуры (рис. 93, а). Когда прямоугольники пересекаются (рис. 93,б), требуется дополнительный анализ.
Объемлющий прямоугольник строится следующим образом: прямоугольник должен полностью заключать в себефигуру и иметь стороны, параллельные осям координат. При этом стремятся определить прямоугольник, имеющий наименьшую площадь. Такой прямоугольник легко построить для многих геометрических фигур, например для отрезка прямой, треугольника, окружности (рис. 93, в) и т. д. Более сложно строить объемлющее прямоугольники для дуг окружностей или друшх кривых.
899 Даны натуральные числа n, x1, y1, x2, y2,..., xn, yn. Построить точки с координатами (x1, y1) (x2, y2) (xn, yn) и примоугольник, обьемлющий все эти точки.
Воспользоваться тем, что левый верхний и правый нижний углы искомого прямоугольника имеют координаты (l,t) и (r,b), где
900 При работе с графическим изображением часто возникает необходимость выбрать одну или несколько точек экрана. Так, например, для того чтобы построить отрезок, следует задать два его конца, для построения окружности можно задать ее центр и любую точку на окружности и т. д. Для указывания требуемой точки обычно используют курсор. Курсор может иметь одну, из следующих конфигураций:
Реализовать процедуры для управления с клавиатуры курсором каждого из типов, описанных в предыдущей задаче.
902 Выбор нужной точки экрана обычно выполняется подводом курсора к этой точке и нажатием клавиши "ввод". Иногда бывает полезно видеть и предыдущую выбранную точку-последнюю точку, зафиксированную клавишей "ввод", и новую точку, на которую указывает курсор. Для этого используются метод резиновой нити и метод резинового прямоугольника.
903 Построить треугольник по заданным вершинам. Точки экрана, являющиеся вершинами треугольника, указываются с клавиатуры по методу резиновой нити (см. предыдущую задачу).
904 Построить окружность по двум заданным точкам: центру и одной из точек окружности. Обе точки указываются с клавиатуры по методу резинового прямоугольника (см. задачу 900).
905 Построить прямоугольник по двум заданным точкам: левому верхнему и правому нижнему углам. Обе точки указываются с клавиатуры (см. задачу 900).
906 Построить ломаную по заданным вершинам. Вершины указываются с клавиатуры (см. задачу 900).
907 Составить программу для управления размерами окружности и ее положением на экране. Исходная окружность имеет центр в точке (100, 100) и радиус r = 20. Управление выполняется клавишами:
"ввод" завершает работу программы.
908 Составить программу для управления размерами прямоугольника и его положением на экране. Левый верхний угол исходного прямоугольника расположен в точке (50,50), правый нижний-в точке (100, 100). Управление выполняется клавишами:
"ввод" завершает работу программы.
909 Составить программу для произвольного рисования на экране. Рисунок - это след курсора, перемещаемого с помощью клавиш управления курсором. Должны обеспечиваться возможность стирания изображения и режим, в котором курсор не оставляет след.
910 Составить программу "электронный калейдоскоп". Построение калейдоскопа выполнять следующим образом. В центре экрана должен быть изображен правильный шестиугольник ABCDEF, вершины которого соединены с его центром О (рис. 97). Треугольник FOA должен быть рассечен несколькими прямыми, количество и расположение которых выбирается с помощью датчика случайных чисел. Каждая из полученных таким образом частей треугольника FOA должна быть закрашена цветом, номер которого также выбирается с помощью датчика случайных чисел. После этого изображение в каждом следующем треугольнике (при движении по или против часовой стрелки) должно быть получено симметричным отображением изображения, сформированного ранее в каждом предыдущем треугольнике, относительно их общей стороны: так, изображение в треугольнике АOВ должно быть получено симметричным отображением изображения, сформированного в треугольнике относительно стороны ОА; изображение в треугольнике BОС должно быть получено симметричным отображением изображения, уже сформированного в треугольнике АОВ, относительно стороны OВ и т. д.
*) При решении задач 843-846, 849 на построение графиков функций следует предварительно выбрать расположение координатных осей и масштаб на них. Выбор подходящей системы координат необходим также в задачах 847, 848, 850-854 на построение кривых, заданных уравнениями того или иного вида. В дальнейшем в зависимости от характера задачи может применяться либо специально подобранная, либо экранная система координат.
**) Параметрическое представление кривой l на плоскости с координатами х, у - это две функции x = x(t), y = y(t), определенные на одном и том же числовом множестве.
-
Дано натуральное n. Получить кривую дракона порядка n.
857 Даны натуральные числа n и r. Построить n точек, являющихся вершинами правильного n - угольника, вписанного в окружность радиуса r, и соединить каждую из точек со всеми остальными n-1 точками. Координаты точек задаются формулами xi = r cos(2πi/n), yi = r sin(2πi/n) (i = 1, 2, ..., n). Во избежании повторного вычерчивания линий, соединяющих одни и те же точки, каждую точку с номером i следует соединять толко с теми точками с номерами j для которых выполнено условие i < j.
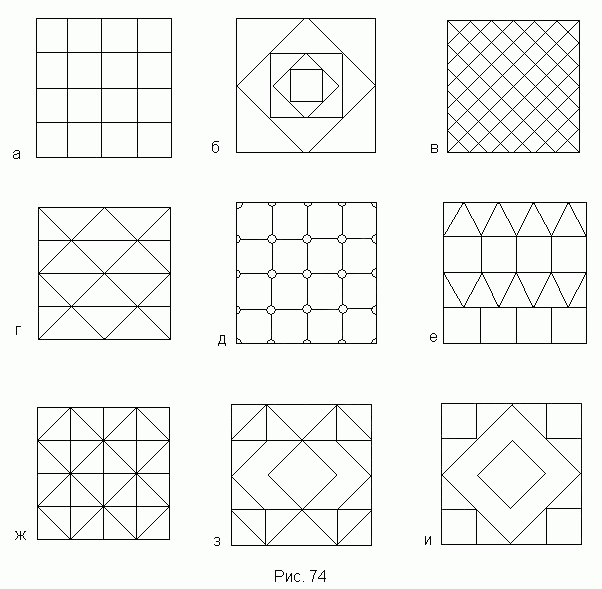
858 Дано натуральное число r. Построить фигуры, показанные на рис. 75, а - 75, г. Фигуры образованы окружность радиуса r и восемью точками, являющимися вершинами правильного многоугольника, вписанного в эту окружность, и соединенных между собой определенным образом. Фигура на рис. 75, а - это правильный восьмиугольник, образованный последовательным соединением его вершин. Для построения фигуры на рис. 75, б следует соединять вершины многоугольника через одну. При построении фигуры на рис. 75, в соединяются вершины, отстоящие друг от друга на две вершины, а при построении фигуры на рис. 75, г-отстоящие на три вершины.
859 Даны натуральные числа n и r. Построить квадрат, длина стороны которого равна r. Разместить по одной точке в каждом углу квадрата и по n-1 точек на каждой его стороне. Расстояния между соседними точками на любой из сторон должны быть одинаковыми и равными r/n. Тем самым будет построено всего 4n точек, которые можно занумеровать числами 1, ..., 4n (нумерация начинается с левого верхнего угла квадрата и выполняется последовательно). Соединить каждую точку с номером i со всеми точками с номерами j (i,j = 1,..., 4n) такими, что j > i и разность j-i есть число Фибоначчи, меньшее 4n (см. задачу 144).
860 Уравнение f(х, у) = 0, представляющее все точки (х, у) некоторой кривой, называют уравнением кривой в неявной форме. Если кривая делит плоскость на две части, то уравнение в неявной форме позволяет определить, лежит ли точка на кривой, или если нет, то в какой части она лежит (см. задачу 52).
- Даны натуральные числа r, xc,
yc, n, a0, ..., a2n-1. Числа г, xc, yc
задают окружность радиуса г с центром в точке (xc, yc). Пары чисел
ai, ai+1 (i кратно 2) являются координатами точек.
-
а) Построить окружность и все точки, заданные последовательностью
a0, ..., a2n-1 и лежащие вне окружности.
б) Построить окружность и все точки, заданные последовательностью a0, ..., a2n-1 и лежащие внутри окружности.
в) Построить окружность и все точки, заданные последовательностью a0, ..., a2n-1 и не принадлежащие окружности. Точки, лежащие вне окружности и внутри нее, должны иметь разные цвета.
861 Даны натуральные числа а, b, с, n,a0, ..., a2n-1. Числа а, b, с задают прямую l с уравнением ax + by + с = 0. Пары чисел ai, ai+1 (i кратно 2) являются коордннатами точек.
-
а) Построить прямую l и все точки, заданные последовательностью
a0, ..., a2n-1 и тажие, что ах+bу + с < 0.
б) Построить прямую l и вcе точки, заданные последовательностью a0, ..., a2n-1 и такие, что ах+by+с> 0.
в) Построить прямую l и все точки, заданные последовательностью a0, ..., a2n-1 и не принадлежащие прямой l. Точки, лежащие по разные стороны от прямой, должны иметь разные цвета.
- Даны натуральные числа а, b, с, n,
a0, ..., a2n-1 действительное число r. Числа а, b, с определяют прямую с уравнением
ах + by + с = 0. Пары чисел ai, ai+1 (i кратно 2) являются координатами точек.
-
а) Построить прямую l и все точки, заданные последовательностью
a0, ..., a2n-1 не принадлежащие прямой l и такие, что длина перпендикуляра,
опущенного из точки на прямую, меньше r.
б) Построить прямую l и все точки, заданные последовательностью a0, ..., a2n-1 не принадлежащие прямой l и такие, что длина перпендикуляра, опущенного из точки на прямую, больше r.
в) Построить прямую l и все точки, заданные последовательностью a0, ..., a2n-1 и не принадлежащие прямой l. Точки, для которых длина перпендикуляра, опущенного на прямую, меньше r и больше r, должны быть окрашены в разные цвета.
863 Пусть дана система линейных неравенств
-
a1x + b1y + c1 ≥ 0,
a2x + b2y + c2 ≥ 0,
. . . . . . . . . . . . . . . .
amx + bmy + cm ≥ 0.
- Каждое из неравенств этой системы определяет в координатной плоскости
некоторую полуплоскость. Если какие-либо числа х и y удовлетворяют всем неравенствам системы,
то точка (х, у) принадлежит пересечению указан-ныж полуплоскостей. Граница этого пересечения
может состоять из отрезков, полупрямых и целых прямых. В том случае, когда граница состоит
только из отрезков, пересечение полуплоскостей является выпуклым многоугольником (мы здесь
называем многоугольником не только границу, но и все множество точек, охваченное границей).
Обратно, любой выпуклый многоугольник, принадлежащий координатной плоскости, может быть
описан системой линейных неравенств. Пусть A1, ..., An - последовательные
вершины выпуклого многоугольника, из которых никакие три не , лежат на одной прямой. Mожно
выписать уравнение a1x + b1y + c1 = 0 прямой, проходящей через
точки A1, A2. Так как многоугольник выпуклый, то все вершины A3,
..., An лежат в одной полуплоскости относительно этой прямой. Поэтому в качестве
первого неравенства можно взять a1x + b1y + c1 ≥ 0 или
-a1x - b1y - c1 ≥ 0 в зависимости от того, является или
нет положительным числом результат подстановки в a1x + b1y +
c1 координат какой-либо из точек A3, A4, ..., An.
Аналогичным образом следует поступать с уравнениями прямых, проходящих через точки
A2, A3 и т.д. (последние две точки- An,
A1).
- Даны натуральные числа n, a0, ..., a2n-1.
Пары чисел ai , ai+1, (i кратно 2), являются координатами точек.
Рассматривается граница l выпуклого многоугольника с вершинами в точках (36, 30),
(30, 27), (24, 30), (30, 39). Построить l, а также точки, заданные последовательностью
a0, ..., a2n-1
-
а) лежащие вне многоугольника;
б) лежащие внутри многоугольника, но не на l;
в) принадлежащие l (точки выделить цветом, отличным от цвета l);
г) лежащие где-либо на плоскости; те точки, которые лежат внутри многоугольника, на его границе и вне его, должны иметь разные цвета, ни один из которых не совпадает с цветом границы.
864 Пусть две точки заданы своими координатами (x1, y1) и (x2, y2). Прямая, проходящая через эти две точки, может быть описана следующими параметрическими уравнениями:
-
x = x1 + (x2 - x1) t, y = y1 +
(y2 - y1)
- При 0 < t < 1 точка (х, у) лежит внутри отрезка и делит его в отношении
t / (1-t); при t = 0 достигается конец отрезка (x1, y1),
при t = 1 - конец (x2,
y2). При t > 1 точка (х, у) лежит на прямой вне отрезка с той же стороны от (x1,
y1), что и (x2, y2); при t < 0 - с противоположной стороны.
-
Даны натуральные числаx1, y1,x2,
y2 действительное число µ (0 ≤ µ < 1). Построить отрезок с координатами концов
(x1, y1), (x2, y2) и точку, делящую отрезок в отношении
µ/(1-µ).
865 Начертить узор, показанный на рис. 76. Узор образован 20 вложенными квадратами. Стороны первого квадрата параллельны осям координат экрана и равны 60. Вершины каждого последующего квадрата - это точки на сторонах предыдущего квадрата, делящие эти стороны в отношении µ = 0,08 (см. предыдущую задачу).
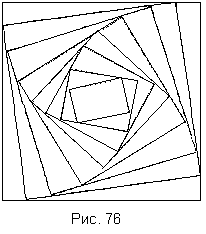
866 Начертить узор, повторяющий узор, описанный в предыдущей задаче, но составленный из
-
а) треугольников;
б) пятиугольников;
в) шестиугольников.
867 Построить узор, показанный на рис. 77, используя алгоритм, описанный в задаче 864.
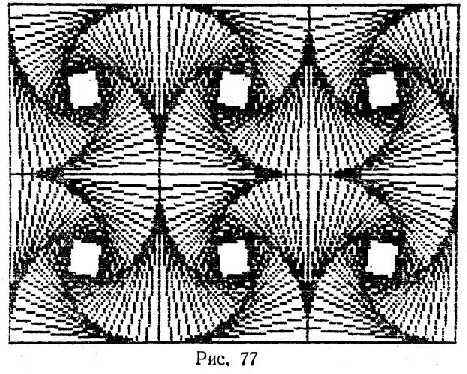
868 Даны натуральные числа x1, y1,x2, y2.Начертить штриховые линии между точками (x1, y1) и (x2, y2) так, как показано на рис. 78. Способ определения координат с концами (x1, y1) и (x2, y2) и делящей отрезок в заданном отношении, см. в задаче 864.

869 Даны натуральные числа x1, y1,x2, y2,x3, y3,x4, y4. Построить две прямые, одна из которых проходит через точки с координатами (x1, y1) и (x2, y2), а другая - через точки с координатами (x3, y3) и (x4, y4). Построить точку пересечения этих прямых, если она существует, и определить, лежит ли точка пересечения внутри отрезков с концами (x1, y1), (x2, y2) и x3, y3, x4, y4 или вне их (см. задачу 864).
870 Даны целые числа t1, t2, ..., t31. Последовательность значений t1, t2, ..., t31 задает график температур за март месяц, подобный показанному на рис. 79. Построить график температур. Отрезки прямых, лежащие выше горизонтальной прямой, соответствующей нулевой температуре, и лежащие ниже зтой прямой, должны быть окрашены в разные цвета.
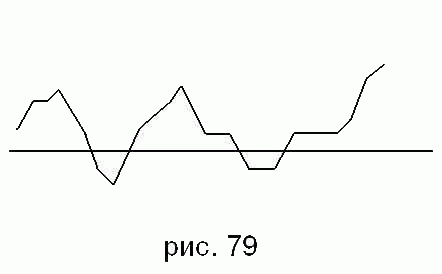
871 даны натуральные числа x1, y1, x2, y2, x3, y3. Построить отрезок с координатами окнцов (x1, y1) и (x2, y2), а также отрезок, параллельный и равный по длине первому отрезку; один конец отрезка должен иметь координаты(x4, y4), второй следует расположить:
-
а) по ту же сторону от (x3, y3), что и (x2, y2) от
(x1, y1);
б) с противоположной стороны.
- Воспльзоваться тем, что параметрические уравнения прямой, проходящей
через точку (x3, y3) и параллельной прямой, проходящей через точки
(x1, y1) и (x2, y2), могут иметь вид
x = x3 + (x2 - x1)t, y = y3 + (y2 -
y1)t
- Координаты конца искомого отрезка вычисляются подстановкой значений
t = 1 и t = -1. При t = 1 конец отрезка будет расположен на прямой с той же стороны от (x3,
y3), что и точка (x2, y2) от точки (x1, y1);
при t = - 1 - с про тивоположной.
872 Даны натуральные числа x1, y1,x2, y2, x3, y3. Построить отрезок с координатами концов (x1, y1) и (x2, y2). Через точку (x3, y3) провести отрезок, таким образом, чтобы точка (x3, y3) делила искомый отрезок пополам (см. предыдущую задачу и задачу 864).
873 Даны натуральные числа xc, yc,h,ω, x, y. Построить прямоугольник с центром в точке (xc, yc), высотой h и шириной ω, а также отрезок прямой с координатами концов (xc, yc) и (x,y). Отметить точку пересечения отрезка со стороной прямоугольника (рис. 80).

874 Даны натуральные числа xc, yc,h,ω, x, y. Построить прямоугольник с центром в точке(xc, yc), высотой h и шириной ω, а также определить координаты xp, yp точки пересеченмя невидимой прямой, проходящей через точки (xc, yc) и (x, y) (см. предыдущую задачу). Кроме того построить:
-
a) отрезок прямой с координатами концов (xc, yc) и
(xp, yp) (рис. 81, а);
б) отрезок прямой с координатами концов (xc, yc) и (xp, yp) (рис. 81, б);
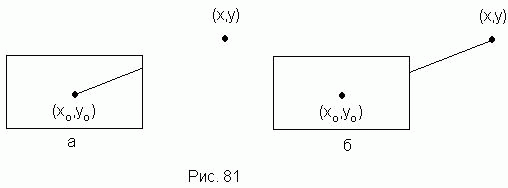
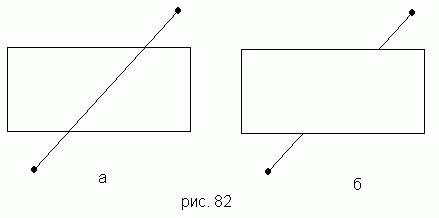
875 Прямоугольник задан координатами левого верхнего и правого нижнего угла, отрезок - координатами концов. Предполагается, что отрезок пересекает противоположные стороны прямоугольника так, как показано на рис. 82, а. Построить фигуру, изображенную на рис. 82, б (см. задачу 873).
876 Даны натуральные числа xc, yc, r, x, y. Построить окружность с центром в точке (xc, yc) и радиусом r, а также отрезок с координатами концов (xc, yc) и (x, y). Отметить точку пересечения отрезка и окружности.
- Воспользоваться тем, что прямая,
проходящая через точки (x1, y1) и (x2, y2), может быть описана
параметрическими уравнениями x = x1 + et, y = y1 + ft, где
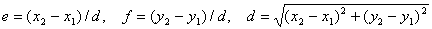 .
.- Такой способ задания прямой
отличается от указанного в задаче 864 тем, что при t = 1 мы получаем не второй конец отрезка
(x2, y2), как в задаче 864, а точки, отстоящую от конца (x1, y1)
на единичное расстояние. Из этого следует, что координаты точки пересечения отрезка с окружностью могут
быть вычислены подстановкой в данные параметрические уравнения значения t = r, где r - радиус окружности.
877 Даны натуральные числа xc, yc, r, x, y. Построить окружность с центром в точке (xc, yc) и радиусом r, а также определить координаты xp, yp точки пересечения с окружностью невидимой прямой, проходящей через точки (xc, yc) и (x,y). Кроме того, построить отрезок с координатами концов:
-
а) (xc, yc) и (xp, yp);
б) (x, y) и (xp, yp).
- Отметить точку пересечения отрезка и окружности.
878 Даны натуральные числа x1, y1, x2, y2, действительное µ(0 < µ < 1). Построить отрезок с координатами концов (x1, y1), (x2, y2) и восстановить перпендикуляр к отрезку из точки (x3, y3), делящей его в отношении µ/(1-µ).
- Воспользоваться тем, что прямая,
перпендикулярная отрезку с концами (x1, y1), (x2, y2) и проходящая
через точку (x3, y3), описывается параметрическими уравнениями
x = x3 - f t, y = y3 + et или x = x3 + f t,
y = y3 - et, где
 .
.-
Расстояние произвольной точки на этой прямой от точки (x3, y3) определяется
параметром t (см. также задачу 864).
879 Даны натуральные числа x1, y1, x2, y2, x3, y3. Построить отрезок с координатами концов (x1, y1), (x2, y2) и опустить на него или не на его продолжение перпендикуляр из точки (x3, y3) (см. предыдущую задачу и задачу 876).
880 Даны натуральные числа x1, y1, x2, y2. Построить отрезок с координатами концов (x1, y1), (x2, y2) и какой-нибудь отрезок, параллельный и равный по длине первому отрезку и отстоящему от него на 30 единиц (см. задачи 871 и 878).
881 Пусть стрелка, соединяющая две произвольные точки, устроена, как в задаче 127. Даны натуральные числа x1, y1, x2, y2. Построить стрелку, направленную из точки (x1, y1) в точку (x2, y2). (Способ определения координат точки, лежащей на отрезке с заданными концами и делящей отрезок в заданном отношении, см. в задаче 864. Способ построения прямой, перпендикулярной данной, см. в задаче 878.)
882 Даны натуральные числа x, y, r, x1, y1, h, ω. Построить окружность радиуса r с центром в точке (x, y), прямоугольник с центром в точке (x1, y1), высотой h и шириной ω, а также отрезок, соединяющий центр окружности с центром прямоугольника (рис. 83).
883 Даны натуральные числа x,y,r,x1, y1, h, ω. Построить окружность радиуса r с центром в точке (x,y), прямоугольник с центром в точке (x1, y1), высотой h и шириной ω, а также отрезок, соединяющий центр окружности с центром прямоугольника. Отрезок должен лежать на невидимой прямой с окружностью и заканчиваться в точке пересечения прямой с прямоугольником (рис. 84).
- (Способ
определения координат точек пересечения прямой, проходящей через две заданные точки, с окружностью
и прямоугольником см. в задачах 876 и 873.)
884 Даны натуральные числа x, y, n, символы S1, ..., Sn. Последовательность символов S1, ..., Sn вывести так, чтобы точка с координатами (x, y) была расположена (рис. 85):
-
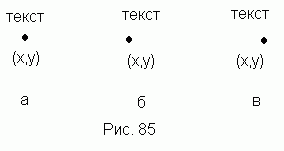
а) по центру последовательности;
б) с левого края последовательности;
в) с правого края последовательности;
885 Пусть в двумерной декартовой системе координат задана плоская фигура и пусть (x, y) - координаты одной из ее точек. Рассмотрим, как изменятся эти координаты, если к фигуре применить одно из следующих преобразований:перенос вдоль осей координат, поворот вокруг начала координат, растяжение (сжатие) по осям координат.
-
1) Перенос на tx единиц по оси ОХ и ty единиц по оси OY:
(x, y) → (x - tx, y - ty)
2) Растяжение (сжатие) по оcи OX в sx раз и по оси ОУ sy раз: (x, y) → (sx, sy)
3) Поворот вокруг начала крординат на угол t радиан: (x, y) → (x cos t + y sin t, -x sin t + y cos t).
- Треугольник задан координатами вершин. Построить его, а затем перенести
на десять единиц по оси ОХ и на пять единиц по оси ОУ.
886 Даны натуральные числа xc, yc, r и действительное число t. Построить правильный пятикгольник, вписанный в окружность с центром в точке (xc, yc) радиусом r, после чего повернуть его от ординат на угол t радиан (см.предыдущую задачу).
887 Даны натуральные числа xc, yc, r, sx, sy. Построить правильный шестиугольник с центром в точке (xc, yc) и стороной r, после чего растянуть (сжать) его по оси OX в sx раз, а по оси OY - в sy раз (см. задачу 885).
888 Построить фигуру, изображенную на рис. 86. В центре фигуры находятся с заданной стороной (см. задачу 885).
889 Выполнить задания а) - е) задачи 849, после чего применить к построенным фигурам следующие преобразования:
-
а) перенос по оси ОХ на 10 единиц в направлении, обратном направлению оси;
б) поворот относительно начала координат на угол π/4 радиан;
в) растяжение (сжатие) по оси OY в два раза (см. задачу 885).
890 Построить спираль, описанную в задаче 851, после чего применить к ней преобразования а) - в) предыдущей задачи.
891 Даны натуральные числа xc, yc, a, b и действительное t. Начертить эллипс с центром в точке (xc, yc), большой осью a, малой осью b; большая ось образует угол t радиан с положительной полуосью ОХ
(рис. 87).
- Воспользоваться следующим алгоритмом. Построить эллипс с центром
в начале координат, с большой и малой осями, совпадающими с осями ОХ и OY системы координат
(параметрические уравнения такого эллипса даны в задаче 849). После чего применить к эллипсу
следующие преобразования; поворот на угол t радиан и перенос по оси ОХ на xc
единиц, по оси OY - на yc единиц
(см. задачу 885).
892 Даны натуральные числа xc, yc, r и действительное число t. Начертить астроиду радиуса r с центром в точке (xc, yc), где одна из осей фигуры составляет угол t радиан с положительной полуосью ОХ (рис. 88). (См. задачи 849 и 885.)

893 Один из возможных способов построения на экране букв произвольного размера был описан в задаче 131. Другой достаточно широко распространенный способ заключается в том, что буквы строятся из отдельных отрезков, размещаемых в соответствии с конфигурацией буквы в прямоугольнике определенного размера, подобно тому,это делается при написании цифр на электронных часах или индекса на почтовом конверте (рис. 89). Если предположить, что левый нижний угол прямоугольника совмещен с началом координат, то каждому отрезку можно поставить в соответствие координаты его концов. Так, букве Б, изображенной на рис. 90, соответствует последовательность координат (0, 0)-(0, 8), (0, 8) - (4, 8), (0, 4)- (4,4), (0,0) - (4,0), (4,4)-(4,0)-назовем ее векторным шаблоном буквы. Таким образом, последующая обрисовка буквы на экране сводится к построению отрезков, координаты концов которых определяются согласно векторному шаблону и с учетом позиции экрана, в которую должен быть помещен левый нижний угол соответствующего прямоугольника. (Перенос и другие преобразования фигур описаны в задаче 885.)
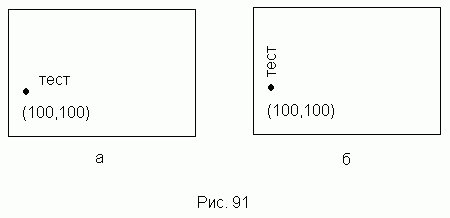
-
Составить векторные шаблоны для всех букв алфавита и цифр и получить на экране слова ТЕСТ, расположенное,
как показано на рис. 91, а и 91, б.
894 Используя шаблоны, описанные в предыдущей задаче, выполнить подрисуночные подписи к графикам функций из задач 843-849.
895 Даны натуральные числа x1, y1x2, y2x3, y3x4, y4. Построить прямоугольник, левый верхний угол которого находится в точке (x1, y1), а правый нижний - в точке (x2, y2), и прямоугольник, левый верхний угол которого находится в точке (x3, y3)" а правый нижний - в точке (x4, y4). Определить, пересекаются ли эти прямоугольники. Если да, то закрасить их общую часть.
Для решения задачи воспользовался следующим. Пусть
l = max(x1, x3),
r = min(x2, x4),
b = max(y2, y4),
t = min(y1, y3).
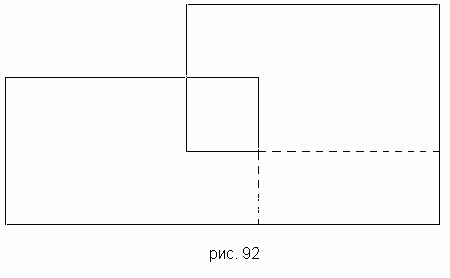
896 Два прямоугольника заданы координатами своих левого верхнего и правого нижнего углов. Верно ли что прямоугольники пересекаются и что первый из них расположен левее и ниже, чем второй? Если да, то построить фигуру, показанную на рис, 92 (см. предыдущую задачу).
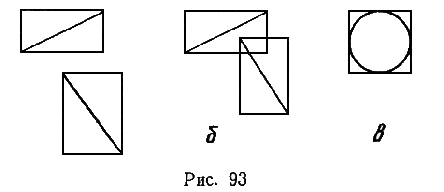
897 Вопрос о том, пересекаются ли две (или более) плоские геометрические фигуры, отчасти может быть сведен к более простому вопросу о том, пересекаются ли прямоугольники, объемлющие эти фигуры. В случае, когда прямоугольники не пересекаются, не пересекаются и сами фигуры (рис. 93, а). Когда прямоугольники пересекаются (рис. 93,б), требуется дополнительный анализ.
Объемлющий прямоугольник строится следующим образом: прямоугольник должен полностью заключать в себефигуру и иметь стороны, параллельные осям координат. При этом стремятся определить прямоугольник, имеющий наименьшую площадь. Такой прямоугольник легко построить для многих геометрических фигур, например для отрезка прямой, треугольника, окружности (рис. 93, в) и т. д. Более сложно строить объемлющее прямоугольники для дуг окружностей или друшх кривых.
а) Отрезок прямой задан координатами концов. Построить прямоугольник, объемлющий данный отрезок.
б) Окружность задана координатами центра и радиусом. Построить квадрат, объемлющей данную окружность.
в) Треугольник задан координатами вершин. Построить прямоугольник, объемлющий данный треугольник.
-
l = min (l1,..., ln)
r = max (r1,..., rn)
b = min (b1,..., bn)
t = max (t1,..., tn)
899 Даны натуральные числа n, x1, y1, x2, y2,..., xn, yn. Построить точки с координатами (x1, y1) (x2, y2) (xn, yn) и примоугольник, обьемлющий все эти точки.
Воспользоваться тем, что левый верхний и правый нижний углы искомого прямоугольника имеют координаты (l,t) и (r,b), где
-
l = min (x1, x2, ..., xn)
r = max (x1, x2, ..., xn)
b = min (y1, y2, ..., yn)
t = max (y1, y2, ..., yn)
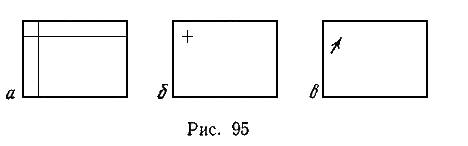
900 При работе с графическим изображением часто возникает необходимость выбрать одну или несколько точек экрана. Так, например, для того чтобы построить отрезок, следует задать два его конца, для построения окружности можно задать ее центр и любую точку на окружности и т. д. Для указывания требуемой точки обычно используют курсор. Курсор может иметь одну, из следующих конфигураций:
-
а) Перекрестье (рис. 95, а). Указываемая точка-это точка пересечения двух прямых.
б) Крестик (рис. 95,6). Указываемая точка-это точка пересечения двух коротких отрезков.
в) Стрелка (рис. 95, б). Указываемая точка-это точка, в которую помещается острие стрелки.
Реализовать процедуры для управления с клавиатуры курсором каждого из типов, описанных в предыдущей задаче.
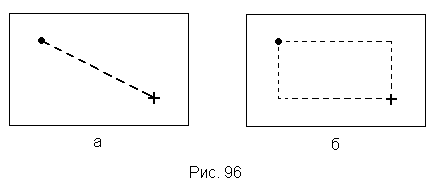
902 Выбор нужной точки экрана обычно выполняется подводом курсора к этой точке и нажатием клавиши "ввод". Иногда бывает полезно видеть и предыдущую выбранную точку-последнюю точку, зафиксированную клавишей "ввод", и новую точку, на которую указывает курсор. Для этого используются метод резиновой нити и метод резинового прямоугольника.
-
а) В методе резиновой нити (рис. 96, а) один конец отрезка зафиксирован и указывает последнюю
выбранную точку, второй конец перемещается в соответствии с изменением указываемой точки.
б) В методе резинового прямоугольника (рис. 96,6) один угол прямоугольника зафиксирован и указывает последнюю выбранную точку, а противолежащий угол перемещается в соответствии с изменением указываемой точки.
903 Построить треугольник по заданным вершинам. Точки экрана, являющиеся вершинами треугольника, указываются с клавиатуры по методу резиновой нити (см. предыдущую задачу).
904 Построить окружность по двум заданным точкам: центру и одной из точек окружности. Обе точки указываются с клавиатуры по методу резинового прямоугольника (см. задачу 900).
905 Построить прямоугольник по двум заданным точкам: левому верхнему и правому нижнему углам. Обе точки указываются с клавиатуры (см. задачу 900).
906 Построить ломаную по заданным вершинам. Вершины указываются с клавиатуры (см. задачу 900).
907 Составить программу для управления размерами окружности и ее положением на экране. Исходная окружность имеет центр в точке (100, 100) и радиус r = 20. Управление выполняется клавишами:
-
">" увеличивает радиус окружности на 5 точек;
"<" уменьшает радиус окружности на 5 точек;
"ввод" завершает работу программы.
908 Составить программу для управления размерами прямоугольника и его положением на экране. Левый верхний угол исходного прямоугольника расположен в точке (50,50), правый нижний-в точке (100, 100). Управление выполняется клавишами:
- ">" увеличивает ширину прямоугольника на 5 точек;
"<" уменьшает ширину прямоугольника на 5 точек;
~ " + " увеличивает высоту прямоугольника на 5 точек;
"-" уменьшает высоту прямоугольника на 5 точек;
"ввод" завершает работу программы.
909 Составить программу для произвольного рисования на экране. Рисунок - это след курсора, перемещаемого с помощью клавиш управления курсором. Должны обеспечиваться возможность стирания изображения и режим, в котором курсор не оставляет след.
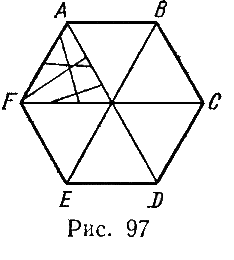
910 Составить программу "электронный калейдоскоп". Построение калейдоскопа выполнять следующим образом. В центре экрана должен быть изображен правильный шестиугольник ABCDEF, вершины которого соединены с его центром О (рис. 97). Треугольник FOA должен быть рассечен несколькими прямыми, количество и расположение которых выбирается с помощью датчика случайных чисел. Каждая из полученных таким образом частей треугольника FOA должна быть закрашена цветом, номер которого также выбирается с помощью датчика случайных чисел. После этого изображение в каждом следующем треугольнике (при движении по или против часовой стрелки) должно быть получено симметричным отображением изображения, сформированного ранее в каждом предыдущем треугольнике, относительно их общей стороны: так, изображение в треугольнике АOВ должно быть получено симметричным отображением изображения, сформированного в треугольнике относительно стороны ОА; изображение в треугольнике BОС должно быть получено симметричным отображением изображения, уже сформированного в треугольнике АОВ, относительно стороны OВ и т. д.
*) При решении задач 843-846, 849 на построение графиков функций следует предварительно выбрать расположение координатных осей и масштаб на них. Выбор подходящей системы координат необходим также в задачах 847, 848, 850-854 на построение кривых, заданных уравнениями того или иного вида. В дальнейшем в зависимости от характера задачи может применяться либо специально подобранная, либо экранная система координат.
**) Параметрическое представление кривой l на плоскости с координатами х, у - это две функции x = x(t), y = y(t), определенные на одном и том же числовом множестве.
 Предыдущая глава
Предыдущая глава