424 Даны действительные числа s, t. Получить
.
425 Даны действительные числа s, t. Получить
.
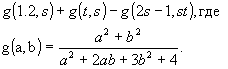426 Дано действительное число y. Получить
.
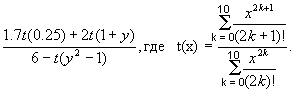427 Даны действительные числа a, b, c. Получить
.
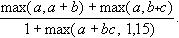428 Даны действительные числа a, b. Получить u = min (ab, a + b), min(u + u2, 3.14).
429 Даны натуральные числа n, m, целые числа a1, ..., an, b1, ..., bm, c1, ..., c30. Получить
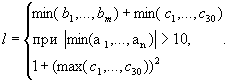в противном случае.
430 Даны натуральные числа k, l, m, действительные числа x 1 , ..., x k , y 1 , y l , z l , z m . Получить
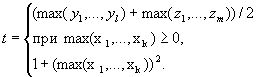в противном случае.
431 Даны действительные числа s, t . Получить
.
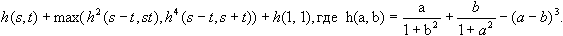432 Даны действительные числа a0, ..., a6. Получить для x = 1, 3, 4 значения p(x + 1) - p(x), где p(y) = a6y6 + a5y5 + ... + a0.
433 Даны действительные числа s, t, a0, ..., a12. Получить
p(1) - p(t) + p2(s - t) - p3(1), где p(x) = a12x12 + a11x11 + a6.
434 Даны действительные числа a1, ..., anb1, ..., bm.В последовательности a1, ..., an и в последовательности b1, ..., bm все члены, следующие за членом с наибольшим значением (за первым по порядку, если их несколько) , заменить на 0.5.
435 Даны целые числа a0, ..., an , b1, ..., bm , k . Если в последовательности a0, ..., an нет ни одного члена со значением k , то первый по порядку член этой последовательности, не меньший всех остальных членов, заменить на значение k . По та кому же правилу преобразовать последовательность b1, ..., bm применительно к значению 10.
436 Даны целые числа n0, d0, n1, d1, ..., n7, d7, b (d0d1...d7b ≠ 0). Вычислить по схеме Горнера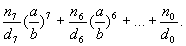
, определив процедуры полного сокращения рационального числа, заданного
числителем и знаменателем, а также процедуры сложения и умножения рациональных чисел.
437 Даны целые числа f0, ..., f10. Исследовать существование целочисленных корней уравнения f10x10 + f9x9 + ... + f0 = 0. (Если f 0 = 0, то имеется корень 0; если же f 0 ≠ 0, то целочисленный корень , если он существует, принадлежит конечному множеству положительных и отрицательных делителей числа f 0 ). Здесь полезно определить процедуру вычисления по схеме Горнера значения многочлена , а также процедуру , которая по двум заданным числам k и m (m > k ≥ 0) позволяет определить значение наименьшего делителя числа m, содержащегося среди чисел k + 1 , k + 2 ,.... m .
438 Даны натуральное число n, действительные числа x, y, an, bn, an-1, bn-1, a0, b0. Вычислить по схеме Горнера значение многочлена с комплексными коэффициентами (an + ibn)(x + iy)n + (an-1 + ibn-1)(x + iy)n-1 + ... + (a0 + ib0) . (Определить процедуры выполнения арифметических операций над комплексными числами.)
439 Даны действительные числа u1, u2, v1, v2, w1, w2. Получить для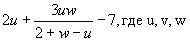
- комплексные числа
u1 + iu2, v1 + iv2, w1 + iw2.
(Определить процедуры выполнения арифметических операций над комплексными числами.)
440 Дано натуральное число n, целые числа a1, ..., an. Рассмотреть отрезки последовательности a1, ..., an (подпоследовательности идущих подряд членов), состоящие из
441 Дано натуральное число n. Среди чисел 1, 2, ..., n найти все те, которые можно представить в виде суммы квадратов двух натуральных чисел. (Определить процедуры, позволяющие распознавать полные квадраты).
442 Даны действительные числа x1, y1, x2, y2, ..., x10, y10. Найти периметр десятиугольника, вершины которого имеют соответственно координаты (x1, y1), ( x2, y2), ..., (x10, y10). (Определить процедуру вычисления расстояния между двумя точками, заданными своими координатами).
443 Даны действительные числа a, b, c, d. Найти площадь пятиугольника, изображенного на рис. 18. (Определить процедуру вычисления площади треугольника по трем его сторонам).
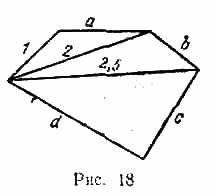
444 Даны натуральное число n, действительные числа x1, y1, x2, y2, ..., xn, yn. Найти площадь n-угольника, вершины которого при некотором последовательном обходе имеют координаты (x1, y1), (x2, y2), ..., (xn, yn). (Определить процедуру вычисления площади треугольника по координатам его вершин).
445 Дано четное число n > 2; проверить для этого числа гипотезу Гольдбаха. Эта гипотеза (по сегодняшний день не опровергнутая и полностью не доказанная)заключается в том, что каждое четное n, большее двух, представляется в виде суммы двух простых чисел. (Определить процедуру, позволяющую распознавать простые числа).
446 Дано натуральное число n. Выяснить, имеются ли среди чисел n, n+1, ..., 2n близнецы, т.е. простые числа , разность между которыми равна двум. (Определить процедуру, позволяющую распознавать простые числа).
447 Дано натуральное число n, целые числа a1, ..., an. Рассмотреть все орезки последовательности a1, ..., an (см. задачу 440), состоящие из совершенных чисел. (Определить процедуру, позволяющую распознавать совершенные числа).
448 Бесконечная последовательность рациональных чисел v0, v1 ,... образована по следующему закону:
449 Даны действительные числа x1, y1, x2, y2, ..., x6, y6. Точки с координатами (x1, y1), (x2, y2), (x3, y3) рассматриваются как вершины первого треугольника, точки с координатами (x4, y4), (x5, y5), (x6, y6) - второго треугольника. Выяснить, верно, ли что первый треугольник целиком содержится во втором, иесли да, определить площадь области, принадлежащей внешнему треугольнику и не принадлежащей внутреннему (на рис. 19 область заштрихована). (Определить процедуру, позволяющую выяснить, лежат ли две точки в одной полуплоскости относительно заданной прямой(см. задач 52), процедуру вычисления расстояния между двумя точками, а также процедуру вычисления площади треугольника по трем сторонам).
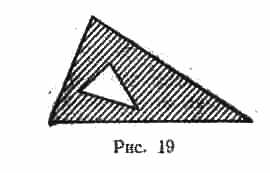
450 Два треугольника заданны координатами своих вершин так, как указано в предыдущей задаче. Выяснить, лежит ли какой-либо из треугольников целиком внутри другого. Если да, построить стороны треугольника и закрасить область, принадлежащую внешнему треугольнику и не принадлежащую внутреннему(рис. 19). Построения сторон и закраску области выполнить одним цветом. Если ни один из треугольников не лежит целиком внутри другого, построить стороны треугольника, используя для каждого треугольника свой цвет. (Определить процедуру, позволяющую выяснить, лежат ли две точки в одной полуплоскости относительно заданной прямой (см. задачу 52) и процедуру построения сторон треугольника по заданным координатам вершин и номеру цвета).
451 Даны натуральные числа x1, y1, x2, y2, ..., x6, y6. Точки с координатами (x1, y1), (x2, y2), (x3, y3) рассматриваются как три вершины первого прямоугольника, точки с координатами (x4, y4), (x5, y5), (x6, y6) - второго. Провести построения, аналогичные тем, которые были описаны в предыдущей задаче в отношении треугольников. Стороны прямоугольников считаются параллельными осям экрана (рис. 20).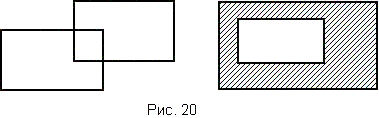
452 Представим себе, что в центре экрана сидит жучок, который может перемещаться по прямой на указанное расстояние и поворачивать направо и налево. У жучка есть перо, которое может оставлять след, повторяющий движение жучка. Если перо опущено, след остается;если перо поднято, следа нет. Итак, жучок может выполнять следующие приказы: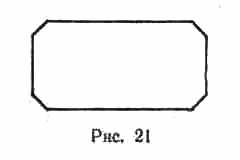
453 Даны натуральные числа k, l, m, символы s1, ..., s30. Вывести данные символы в следующем виде:
454 Дано натуральное число n; найти n!. Использовать программу, включающую рекурсивную процедуру вычисления n!. Чем эта программа хуже нерекурсивной программы вычисления n!?
455 Даны натуральные числа n, m; найти НОД(n, m). Использовать программу, включающую рекурсивную процедуру вычисления НОД, основанную на соотношении НОД(n, m) = НОД(m, r)- остаток от деления n на m(см. задачу 89). Чем эта программа хуже нерекурсивной программы вычисления НОД(n, m)?
456 Числа Фибоначчи u 0, u 1, u 2, ... определяются следующим образом: u 0 = 0, u 1 = 1, u n = u n-1 + u n-2 (n = 2, 3, ...) (см. задачу 144). Написать программу вычисления u n для данного неотрицательного целого n, включающую рекурсивную процедуру, которая основана на непосредственном использовании соотношения u n = u n-1+u n-2. Доказать по индукции, что при вычислении u n (n = 2, 3, ...) по этой программе придется выполнить u n-1 сложение чисел Фибоначчи. Итак, для нерекурсивной программы количество сложений чисел Фибоначчи при вычислении u n для n = 0, 1, ..., 10 есть соответственно 0, 0, 1, 2, 3, 4, 5, 6, 7, 8, а для рекурсивной - 0, 0, 1, 2, 4, 7, 12, 20, 30, 54. Ввиду последнего обстоятельства никогда не следует пользоваться такого рода рекурсивными процедурами, основанными на непосредственном применении соотношений вида x n = f x n-1, ..., x n-k, k ≥ 2.
457 Даны натуральные числа a, c, m. Получить f(m), где
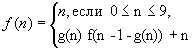в противном случае.
458 Даны неотрицательные целые числа n, m;вычислить А(n, m), где
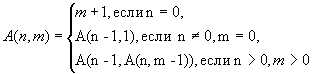
(это-так называемая функция Аккермана). Использовать программу, включающую рекурсивную процедуру.
459 Многие задачи, помещенные в параграфе 9, где речь идет о вложенных циклах, могут решаться с привлечением процедур-внутренние циклы могут быть заменены обращениями к должным образом определенным процедурам. Например, для решении задачи 317 можно определить процедуру вычисления an, для решения задачи 318-процедуру вычисления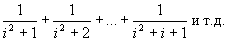
Посмотреть задачи параграфа 9 и сказать,
какие процедуры были бы полезны для решения этих задач.
460 Составить процедуру вычисления значения целого числа по заданной строке символов, являющейся записью этого числа:
461 Составить процедуру построения строки символов, являющейся записью данного действительного числа в десятичной системе счисления; строка должна содержать указанное количество цифр после запятой.
462 Составить процедуру, результатом работы которой является истинное значение, если символ, заданный при обращении к процедуре, -буква, и ложное значение в противном случае.
463 Составить процедуру, результатом работы которой является символ, заданный при обращении к процедуре, если этот символ не является буквой, и соответствующая строчная (малая) буква в противном случае.
464 Составить процедуру <<сжатия>> исходной последовательности символов: каждая последовательность состящая из нескольких вложенний одного и того же символа, заменяется на текст x(k), где x-символ, а k-строка, являющаяся записью числа вхождений символа x в исходную последовательность.
465 Составить процедуру, позволяющую определить позицию самого правого вхождения заданного символа в исходную строку. Если строка не содержит символа, результатом работы процдуры должна быть -1.
466 Составить процедуру, заменяющую в исходной в исходной строке символов все единицы нулями и все нули единицами. Замена должна выполняться, начиная с заданной позиции строки.
467 Составить процедуру, в рерультате обращения к которой из первой заданной строки удаляется каждый символ, принадлежащий и второй заданной строке.
468 Составить процедуру, позволяющую определить позицию самого правого вхождения в заданную строку какого-либо символа из второй заданной строки. Результатом работы процдуры должна быть -1, если первоя строка не содержит ни одного символа, принадлежащего и второй заданной строке.
469 Выравнивание строки заключается в том, что между ее отдельными словами (см. задачу 269) дополнительно вносятся пробелы так, чтобы длина строки стала равной заданной длине (предполагается, что требуемая длина не меньше исходной), а последнее слово строки сдвинулось к ее правому краю. Составить программу выравнивания заданной строки текста.
470 При выводе текстов на экран или печатающее устройство часто используются табуляционные остановки-выделенные позиции строки. Например, при печати таблиц полезно зафиксировать положение столбцов таблицы. Если в исходном тексте встречается символ табуляции tab (например, символ с кодом 9), это означает, что текст, следующий за символом tab, должен печататься со следующей табуляционной остановки, а до нее следует выдавать пробелы. Составить процедуру печати текста с указанной интерпритацией символа tab (предложить зафиксированный набор табуляционных остановок).
.425 Даны действительные числа s, t. Получить
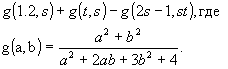.426 Дано действительное число y. Получить
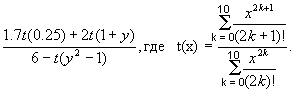.427 Даны действительные числа a, b, c. Получить
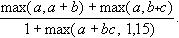.428 Даны действительные числа a, b. Получить u = min (ab, a + b), min(u + u2, 3.14).
429 Даны натуральные числа n, m, целые числа a1, ..., an, b1, ..., bm, c1, ..., c30. Получить
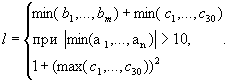в противном случае.430 Даны натуральные числа k, l, m, действительные числа x 1 , ..., x k , y 1 , y l , z l , z m . Получить
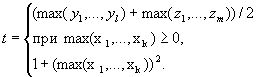в противном случае.431 Даны действительные числа s, t . Получить
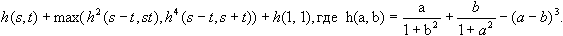.432 Даны действительные числа a0, ..., a6. Получить для x = 1, 3, 4 значения p(x + 1) - p(x), где p(y) = a6y6 + a5y5 + ... + a0.
433 Даны действительные числа s, t, a0, ..., a12. Получить
p(1) - p(t) + p2(s - t) - p3(1), где p(x) = a12x12 + a11x11 + a6.
434 Даны действительные числа a1, ..., anb1, ..., bm.В последовательности a1, ..., an и в последовательности b1, ..., bm все члены, следующие за членом с наибольшим значением (за первым по порядку, если их несколько) , заменить на 0.5.
435 Даны целые числа a0, ..., an , b1, ..., bm , k . Если в последовательности a0, ..., an нет ни одного члена со значением k , то первый по порядку член этой последовательности, не меньший всех остальных членов, заменить на значение k . По та кому же правилу преобразовать последовательность b1, ..., bm применительно к значению 10.
436 Даны целые числа n0, d0, n1, d1, ..., n7, d7, b (d0d1...d7b ≠ 0). Вычислить по схеме Горнера
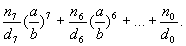, определив процедуры полного сокращения рационального числа, заданного
числителем и знаменателем, а также процедуры сложения и умножения рациональных чисел.437 Даны целые числа f0, ..., f10. Исследовать существование целочисленных корней уравнения f10x10 + f9x9 + ... + f0 = 0. (Если f 0 = 0, то имеется корень 0; если же f 0 ≠ 0, то целочисленный корень , если он существует, принадлежит конечному множеству положительных и отрицательных делителей числа f 0 ). Здесь полезно определить процедуру вычисления по схеме Горнера значения многочлена , а также процедуру , которая по двум заданным числам k и m (m > k ≥ 0) позволяет определить значение наименьшего делителя числа m, содержащегося среди чисел k + 1 , k + 2 ,.... m .
438 Даны натуральное число n, действительные числа x, y, an, bn, an-1, bn-1, a0, b0. Вычислить по схеме Горнера значение многочлена с комплексными коэффициентами (an + ibn)(x + iy)n + (an-1 + ibn-1)(x + iy)n-1 + ... + (a0 + ib0) . (Определить процедуры выполнения арифметических операций над комплексными числами.)
439 Даны действительные числа u1, u2, v1, v2, w1, w2. Получить для
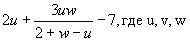- комплексные числа
u1 + iu2, v1 + iv2, w1 + iw2.
(Определить процедуры выполнения арифметических операций над комплексными числами.)440 Дано натуральное число n, целые числа a1, ..., an. Рассмотреть отрезки последовательности a1, ..., an (подпоследовательности идущих подряд членов), состоящие из
-
a) полных квадратов;
б) степеней пятерки;
в) простых чисел.
- В каждом случае получить наибольшую из длин рассматриваемых отрезков. (Определить процедуры,
позволяющие распознавать полные квадраты, степени пятерки, простые числа).
441 Дано натуральное число n. Среди чисел 1, 2, ..., n найти все те, которые можно представить в виде суммы квадратов двух натуральных чисел. (Определить процедуры, позволяющие распознавать полные квадраты).
442 Даны действительные числа x1, y1, x2, y2, ..., x10, y10. Найти периметр десятиугольника, вершины которого имеют соответственно координаты (x1, y1), ( x2, y2), ..., (x10, y10). (Определить процедуру вычисления расстояния между двумя точками, заданными своими координатами).
443 Даны действительные числа a, b, c, d. Найти площадь пятиугольника, изображенного на рис. 18. (Определить процедуру вычисления площади треугольника по трем его сторонам).
444 Даны натуральное число n, действительные числа x1, y1, x2, y2, ..., xn, yn. Найти площадь n-угольника, вершины которого при некотором последовательном обходе имеют координаты (x1, y1), (x2, y2), ..., (xn, yn). (Определить процедуру вычисления площади треугольника по координатам его вершин).
445 Дано четное число n > 2; проверить для этого числа гипотезу Гольдбаха. Эта гипотеза (по сегодняшний день не опровергнутая и полностью не доказанная)заключается в том, что каждое четное n, большее двух, представляется в виде суммы двух простых чисел. (Определить процедуру, позволяющую распознавать простые числа).
446 Дано натуральное число n. Выяснить, имеются ли среди чисел n, n+1, ..., 2n близнецы, т.е. простые числа , разность между которыми равна двум. (Определить процедуру, позволяющую распознавать простые числа).
447 Дано натуральное число n, целые числа a1, ..., an. Рассмотреть все орезки последовательности a1, ..., an (см. задачу 440), состоящие из совершенных чисел. (Определить процедуру, позволяющую распознавать совершенные числа).
448 Бесконечная последовательность рациональных чисел v0, v1 ,... образована по следующему закону:
-
а)
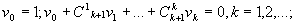;б)
.
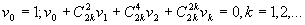- Дано неотрицательное целое число n. Вычислить числитель и знаменатель несократимой формы числа
vn. (Определить процедуры полного сокращения рационального числа, заданного числителем
и знаменателем, а также процедуры сложения и умножения рациональных чисел).
449 Даны действительные числа x1, y1, x2, y2, ..., x6, y6. Точки с координатами (x1, y1), (x2, y2), (x3, y3) рассматриваются как вершины первого треугольника, точки с координатами (x4, y4), (x5, y5), (x6, y6) - второго треугольника. Выяснить, верно, ли что первый треугольник целиком содержится во втором, иесли да, определить площадь области, принадлежащей внешнему треугольнику и не принадлежащей внутреннему (на рис. 19 область заштрихована). (Определить процедуру, позволяющую выяснить, лежат ли две точки в одной полуплоскости относительно заданной прямой(см. задач 52), процедуру вычисления расстояния между двумя точками, а также процедуру вычисления площади треугольника по трем сторонам).
450 Два треугольника заданны координатами своих вершин так, как указано в предыдущей задаче. Выяснить, лежит ли какой-либо из треугольников целиком внутри другого. Если да, построить стороны треугольника и закрасить область, принадлежащую внешнему треугольнику и не принадлежащую внутреннему(рис. 19). Построения сторон и закраску области выполнить одним цветом. Если ни один из треугольников не лежит целиком внутри другого, построить стороны треугольника, используя для каждого треугольника свой цвет. (Определить процедуру, позволяющую выяснить, лежат ли две точки в одной полуплоскости относительно заданной прямой (см. задачу 52) и процедуру построения сторон треугольника по заданным координатам вершин и номеру цвета).
451 Даны натуральные числа x1, y1, x2, y2, ..., x6, y6. Точки с координатами (x1, y1), (x2, y2), (x3, y3) рассматриваются как три вершины первого прямоугольника, точки с координатами (x4, y4), (x5, y5), (x6, y6) - второго. Провести построения, аналогичные тем, которые были описаны в предыдущей задаче в отношении треугольников. Стороны прямоугольников считаются параллельными осям экрана (рис. 20).
452 Представим себе, что в центре экрана сидит жучок, который может перемещаться по прямой на указанное расстояние и поворачивать направо и налево. У жучка есть перо, которое может оставлять след, повторяющий движение жучка. Если перо опущено, след остается;если перо поднято, следа нет. Итак, жучок может выполнять следующие приказы:
-
1) Forward-переместиться на заданное расстояние;
2) Left-повернуть налево на заданный угол;
3) Right-повернуть направо на заданный угол;
4) Pen Up-поднять перо;
5) Pen Down-опустить перо;
- Реализовать процедуры Forward, Left, Right, Pen Up, Pen Down. Процедуры должны взаимодействовать
через глобальные переменные xPOS, yPOS-координаты жучка на экране; Pen-признак, говорящий о том, поднято
перо или опущено; Angle-угол, который образует текущее направление перемещения жучка с осью абсцисс.
С помощью перечисленных процедур получить на экране:
-
a) Квадрат со стороной 75 единиц и центом, совпадающим с центром экрана.
б) Прямоугольник с отношением сторон 1:2 и со срезанными углами. Срезаютя равнобедренные прямоугольные треугольники, катеты которых имеют длину, равную 1/20 длины больщей стороны (рис. 21). Длина меньшей стороны -данная величина. Положение прямоугольника на экране может быть выбрано произвольно.
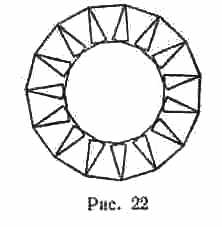
в) Фигуру, составленную из пятнадцати квадратов, которая изображена на рис. 22.
г) Четыре крупные цифры-текущий год; цифры должны быть написаны по девятисегментному шаблону (как на почтовых конвертах).
д) Те же цифры, что и в задании г), но написанные по семисегментному шаблону (как на электронных часах).
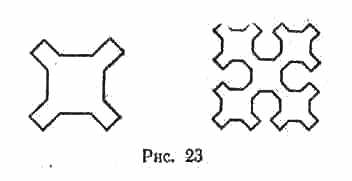
е) Кривые Серпинского порядка 1 и 2, изображенные на рис. 23.
453 Даны натуральные числа k, l, m, символы s1, ..., s30. Вывести данные символы в следующем виде:
- (Определить процедуру, обращение к которой дает вывод символа t после n пробелов).
454 Дано натуральное число n; найти n!. Использовать программу, включающую рекурсивную процедуру вычисления n!. Чем эта программа хуже нерекурсивной программы вычисления n!?
455 Даны натуральные числа n, m; найти НОД(n, m). Использовать программу, включающую рекурсивную процедуру вычисления НОД, основанную на соотношении НОД(n, m) = НОД(m, r)- остаток от деления n на m(см. задачу 89). Чем эта программа хуже нерекурсивной программы вычисления НОД(n, m)?
456 Числа Фибоначчи u 0, u 1, u 2, ... определяются следующим образом: u 0 = 0, u 1 = 1, u n = u n-1 + u n-2 (n = 2, 3, ...) (см. задачу 144). Написать программу вычисления u n для данного неотрицательного целого n, включающую рекурсивную процедуру, которая основана на непосредственном использовании соотношения u n = u n-1+u n-2. Доказать по индукции, что при вычислении u n (n = 2, 3, ...) по этой программе придется выполнить u n-1 сложение чисел Фибоначчи. Итак, для нерекурсивной программы количество сложений чисел Фибоначчи при вычислении u n для n = 0, 1, ..., 10 есть соответственно 0, 0, 1, 2, 3, 4, 5, 6, 7, 8, а для рекурсивной - 0, 0, 1, 2, 4, 7, 12, 20, 30, 54. Ввиду последнего обстоятельства никогда не следует пользоваться такого рода рекурсивными процедурами, основанными на непосредственном применении соотношений вида x n = f x n-1, ..., x n-k, k ≥ 2.
457 Даны натуральные числа a, c, m. Получить f(m), где
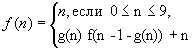в противном случае.- g(n) = остаток от деления a n+c на 10.
- Использовать программу, включающую рекурсивную процедуру вычисления f(n).
458 Даны неотрицательные целые числа n, m;вычислить А(n, m), где
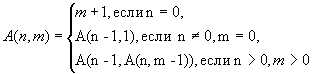
(это-так называемая функция Аккермана). Использовать программу, включающую рекурсивную процедуру.
459 Многие задачи, помещенные в параграфе 9, где речь идет о вложенных циклах, могут решаться с привлечением процедур-внутренние циклы могут быть заменены обращениями к должным образом определенным процедурам. Например, для решении задачи 317 можно определить процедуру вычисления an, для решения задачи 318-процедуру вычисления
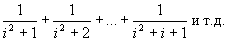Посмотреть задачи параграфа 9 и сказать,
какие процедуры были бы полезны для решения этих задач.460 Составить процедуру вычисления значения целого числа по заданной строке символов, являющейся записью этого числа:
-
а) в десятичной системе счисления;
б) в шестнадцатиричной системе счисления (шестнадцатиричные цыфры-это цифры от 0 до 9 и буквы от A до F).
461 Составить процедуру построения строки символов, являющейся записью данного действительного числа в десятичной системе счисления; строка должна содержать указанное количество цифр после запятой.
462 Составить процедуру, результатом работы которой является истинное значение, если символ, заданный при обращении к процедуре, -буква, и ложное значение в противном случае.
463 Составить процедуру, результатом работы которой является символ, заданный при обращении к процедуре, если этот символ не является буквой, и соответствующая строчная (малая) буква в противном случае.
464 Составить процедуру <<сжатия>> исходной последовательности символов: каждая последовательность состящая из нескольких вложенний одного и того же символа, заменяется на текст x(k), где x-символ, а k-строка, являющаяся записью числа вхождений символа x в исходную последовательность.
465 Составить процедуру, позволяющую определить позицию самого правого вхождения заданного символа в исходную строку. Если строка не содержит символа, результатом работы процдуры должна быть -1.
466 Составить процедуру, заменяющую в исходной в исходной строке символов все единицы нулями и все нули единицами. Замена должна выполняться, начиная с заданной позиции строки.
467 Составить процедуру, в рерультате обращения к которой из первой заданной строки удаляется каждый символ, принадлежащий и второй заданной строке.
468 Составить процедуру, позволяющую определить позицию самого правого вхождения в заданную строку какого-либо символа из второй заданной строки. Результатом работы процдуры должна быть -1, если первоя строка не содержит ни одного символа, принадлежащего и второй заданной строке.
469 Выравнивание строки заключается в том, что между ее отдельными словами (см. задачу 269) дополнительно вносятся пробелы так, чтобы длина строки стала равной заданной длине (предполагается, что требуемая длина не меньше исходной), а последнее слово строки сдвинулось к ее правому краю. Составить программу выравнивания заданной строки текста.
470 При выводе текстов на экран или печатающее устройство часто используются табуляционные остановки-выделенные позиции строки. Например, при печати таблиц полезно зафиксировать положение столбцов таблицы. Если в исходном тексте встречается символ табуляции tab (например, символ с кодом 9), это означает, что текст, следующий за символом tab, должен печататься со следующей табуляционной остановки, а до нее следует выдавать пробелы. Составить процедуру печати текста с указанной интерпритацией символа tab (предложить зафиксированный набор табуляционных остановок).
Предыдущая глава